机器学习sklearn（84）：算法实例（41）分类（20）朴素贝叶斯（三） 不同分布下的贝叶斯（二） 概率类模型的评估指标

1 布里尔分数Brier Score

 

 

from sklearn.metrics import brier_score_loss
#注意，第一个参数是真实标签，第二个参数是预测出的概率值
#在二分类情况下，接口predict_proba会返回两列，但SVC的接口decision_function却只会返回一列
#要随时注意，使用了怎样的概率分类器，以辨别查找置信度的接口，以及这些接口的结构
brier_score_loss(Ytest, prob[:,1], pos_label=1) #我们的pos_label与prob中的索引一致，就可以查看这个类别下的布里尔分数是多少

布里尔分数可以用于任何可以使用predict_proba接口调用概率的模型，我们来探索一下在我们的手写数字数据集上，逻辑回归，SVC和我们的高斯朴素贝叶斯的效果如何： 

from sklearn.metrics import brier_score_loss
brier_score_loss(Ytest,prob[:,8],pos_label=8)
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression as LR
logi = LR(C=1., solver='lbfgs',max_iter=3000,multi_class="auto").fit(Xtrain,Ytrain)
svc = SVC(kernel = "linear",gamma=1).fit(Xtrain,Ytrain)
brier_score_loss(Ytest,logi.predict_proba(Xtest)[:,1],pos_label=1) #由于SVC的置信度并不是概率，为了可比性，我们需要将SVC的置信度“距离”归一化，压缩到[0,1]之间
svc_prob = (svc.decision_function(Xtest) -
svc.decision_function(Xtest).min())/(svc.decision_function(Xtest).max() -
svc.decision_function(Xtest).min())
brier_score_loss(Ytest,svc_prob[:,1],pos_label=1)

如果将每个分类器每个标签类别下的布里尔分数可视化： 

import pandas as pd
name = ["Bayes","Logistic","SVC"]
color = ["red","black","orange"]
df = pd.DataFrame(index=range(10),columns=name)
for i in range(10):
    df.loc[i,name[0]] = brier_score_loss(Ytest,prob[:,i],pos_label=i)
    df.loc[i,name[1]] = brier_score_loss(Ytest,logi.predict_proba(Xtest)
[:,i],pos_label=i)
    df.loc[i,name[2]] = brier_score_loss(Ytest,svc_prob[:,i],pos_label=i)
for i in range(df.shape[1]):
    plt.plot(range(10),df.iloc[:,i],c=color[i])
plt.legend()
plt.show()
df

2 对数似然函数Log Loss

 

 

 

 

from sklearn.metrics import log_loss
log_loss(Ytest,prob)
log_loss(Ytest,logi.predict_proba(Xtest))
log_loss(Ytest,svc_prob)

 

 

 

 

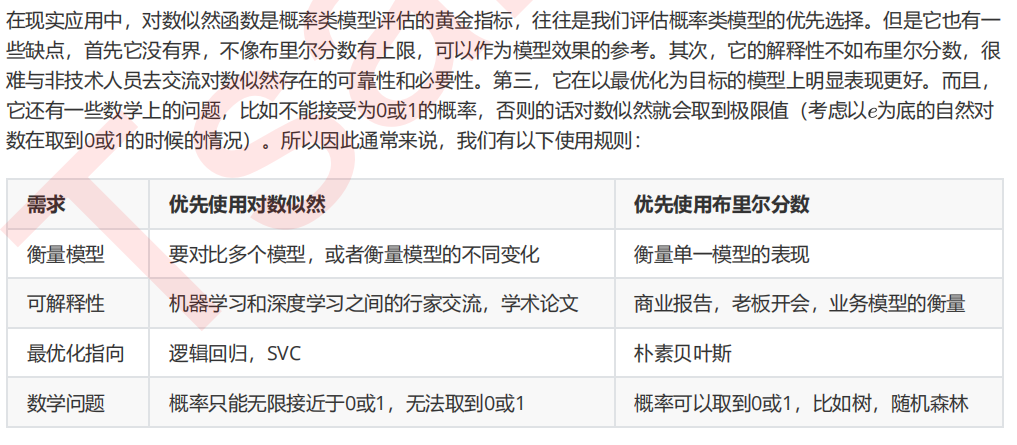
3 可靠曲线Reliability Curve 

1. 导入需要的库和模块 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification as mc
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.metrics import brier_score_loss
from sklearn.model_selection import train_test_split

2. 创建数据集 

X, y = mc(n_samples=100000,n_features=20 #总共20个特征
         ,n_classes=2 #标签为2分类
         ,n_informative=2 #其中两个代表较多信息
         ,n_redundant=10 #10个都是冗余特征
         ,random_state=42) #样本量足够大，因此使用1%的样本作为训练集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y
                                               ,test_size=0.99
                                               ,random_state=42)
Xtrain
np.unique(Ytrain)

3. 建立模型，绘制图像

gnb = GaussianNB()
gnb.fit(Xtrain,Ytrain)
y_pred = gnb.predict(Xtest)
prob_pos = gnb.predict_proba(Xtest)[:,1] #我们的预测概率 - 横坐标
#Ytest - 我们的真实标签 - 横坐标
#在我们的横纵表坐标上，概率是由顺序的（由小到大），为了让图形规整一些，我们要先对预测概率和真实标签按照预测
概率进行一个排序，这一点我们通过DataFrame来实现
df = pd.DataFrame({"ytrue":Ytest[:500],"probability":prob_pos[:500]})
df
df = df.sort_values(by="probability")
df.index = range(df.shape[0])
df
#紧接着我们就可以画图了
fig = plt.figure()
ax1 = plt.subplot()
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated") #得做一条对角线来对比呀
ax1.plot(df["probability"],df["ytrue"],"s-",label="%s (%1.3f)" % ("Bayes", clf_score))
ax1.set_ylabel("True label")
ax1.set_xlabel("predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
plt.show()

fig = plt.figure()
ax1 = plt.subplot()
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
ax1.scatter(df["probability"],df["ytrue"],s=10)
ax1.set_ylabel("True label")
ax1.set_xlabel("predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
plt.show()

 

 

 

 

 

 

 

 

4. 使用可靠性曲线的类在贝叶斯上绘制一条校准曲线 

from sklearn.calibration import calibration_curve
#从类calibiration_curve中获取横坐标和纵坐标
trueproba, predproba = calibration_curve(Ytest, prob_pos
                                         ,n_bins=10 #输入希望分箱的个数
                                       )
fig = plt.figure()
ax1 = plt.subplot()
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
ax1.plot(predproba, trueproba,"s-",label="%s (%1.3f)" % ("Bayes", clf_score))
ax1.set_ylabel("True probability for class 1")
ax1.set_xlabel("Mean predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
plt.show()

5. 不同的n_bins取值下曲线如何改变？

fig, axes = plt.subplots(1,3,figsize=(18,4))
for ind,i in enumerate([3,10,100]):
    ax = axes[ind]
    ax.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
    trueproba, predproba = calibration_curve(Ytest, prob_pos,n_bins=i)
    ax.plot(predproba, trueproba,"s-",label="n_bins = {}".format(i))
    ax1.set_ylabel("True probability for class 1")
    ax1.set_xlabel("Mean predcited probability")
    ax1.set_ylim([-0.05, 1.05])
    ax.legend()
plt.show()

6. 建立更多模型

name = ["GaussianBayes","Logistic","SVC"]
gnb = GaussianNB()
logi = LR(C=1., solver='lbfgs',max_iter=3000,multi_class="auto")
svc = SVC(kernel = "linear",gamma=1)

7. 建立循环，绘制多个模型的概率校准曲线 

fig, ax1 = plt.subplots(figsize=(8,6))
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
for clf, name_ in zip([gnb,logi,svc],name):
    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    #hasattr(obj,name)：查看一个类obj中是否存在名字为name的接口，存在则返回True
    if hasattr(clf, "predict_proba"):
        prob_pos = clf.predict_proba(Xtest)[:,1]
    else:  # use decision function
        prob_pos = clf.decision_function(Xtest)
        prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
    #返回布里尔分数
    clf_score = brier_score_loss(Ytest, prob_pos, pos_label=y.max())
    trueproba, predproba = calibration_curve(Ytest, prob_pos,n_bins=10)
    ax1.plot(predproba, trueproba,"s-",label="%s (%1.3f)" % (name_, clf_score))
    
ax1.set_ylabel("True probability for class 1")
ax1.set_xlabel("Mean predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
ax1.set_title('Calibration plots (reliability curve)')
plt.show()

4 预测概率的直方图

 

 

fig, ax2 = plt.subplots(figsize=(8,6))
for clf, name_ in zip([gnb,logi,svc],name):
    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    #hasattr(obj,name)：查看一个类obj中是否存在名字为name的接口，存在则返回True
    if hasattr(clf, "predict_proba"):
        prob_pos = clf.predict_proba(Xtest)[:,1]
    else:  # use decision function
        prob_pos = clf.decision_function(Xtest)
        prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
    ax2.hist(prob_pos
             ,bins=10
             ,label=name_
             ,histtype="step" #设置直方图为透明
             ,lw=2 #设置直方图每个柱子描边的粗细
           )
    
ax2.set_ylabel("Distribution of probability")
ax2.set_xlabel("Mean predicted probability")
ax2.set_xlim([-0.05, 1.05])
ax2.set_xticks([0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1])
ax2.legend(loc=9)
plt.show()

5 校准可靠性曲线

 

 

 

 

 

 

1. 包装函数

 

 

def plot_calib(models,name,Xtrain,Xtest,Ytrain,Ytest,n_bins=10):
    
    import matplotlib.pyplot as plt
    from sklearn.metrics import brier_score_loss
    from sklearn.calibration import calibration_curve
    
    fig, (ax1, ax2) = plt.subplots(1, 2,figsize=(20,6))
    ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
    for clf, name_ in zip(models,name):
        clf.fit(Xtrain,Ytrain)
        y_pred = clf.predict(Xtest)
        #hasattr(obj,name)：查看一个类obj中是否存在名字为name的接口，存在则返回True
        if hasattr(clf, "predict_proba"):
            prob_pos = clf.predict_proba(Xtest)[:,1]
        else:  # use decision function
            prob_pos = clf.decision_function(Xtest)
            prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
        #返回布里尔分数
        clf_score = brier_score_loss(Ytest, prob_pos, pos_label=y.max())
        trueproba, predproba = calibration_curve(Ytest, prob_pos,n_bins=n_bins)
        ax1.plot(predproba, trueproba,"s-",label="%s (%1.3f)" % (name_, clf_score))
        ax2.hist(prob_pos, range=(0, 1), bins=n_bins, label=name_,histtype="step",lw=2)
    
    ax2.set_ylabel("Distribution of probability")
    ax2.set_xlabel("Mean predicted probability")
    ax2.set_xlim([-0.05, 1.05])
    ax2.legend(loc=9)
    ax2.set_title("Distribution of probablity")
    ax1.set_ylabel("True probability for class 1")
    ax1.set_xlabel("Mean predcited probability")
    ax1.set_ylim([-0.05, 1.05])
    ax1.legend()
    ax1.set_title('Calibration plots(reliability curve)')
    plt.show()

2. 设实例化模型，设定模型的名字

from sklearn.calibration import CalibratedClassifierCV
name = ["GaussianBayes","Logistic","Bayes+isotonic","Bayes+sigmoid"]
gnb = GaussianNB()
models = [gnb
         ,LR(C=1., solver='lbfgs',max_iter=3000,multi_class="auto")
        #定义两种校准方式
         ,CalibratedClassifierCV(gnb, cv=2, method='isotonic')
         ,CalibratedClassifierCV(gnb, cv=2, method='sigmoid')]

3. 基于函数进行绘图 

plot_calib(models,name,Xtrain,Xtest,Ytrain,Ytest)

4. 基于校准结果查看精确性的变化 

gnb = GaussianNB().fit(Xtrain,Ytrain)
gnb.score(Xtest,Ytest)
brier_score_loss(Ytest,gnb.predict_proba(Xtest)[:,1],pos_label = 1)
gnbisotonic = CalibratedClassifierCV(gnb, cv=2, method='isotonic').fit(Xtrain,Ytrain)
gnbisotonic.score(Xtest,Ytest)
brier_score_loss(Ytest,gnbisotonic.predict_proba(Xtest)[:,1],pos_label = 1)

 

 

5. 试试看对于SVC，哪种校准更有效呢？ 

name_svc = ["SVC","Logistic","SVC+isotonic","SVC+sigmoid"]
svc = SVC(kernel = "linear",gamma=1)
models_svc = [svc
             ,LR(C=1., solver='lbfgs',max_iter=3000,multi_class="auto")
              #依然定义两种校准方式
             ,CalibratedClassifierCV(svc, cv=2, method='isotonic')
             ,CalibratedClassifierCV(svc, cv=2, method='sigmoid')]
plot_calib(models_svc,name_svc,Xtrain,Xtest,Ytrain,Ytest)

 

 

name_svc = ["SVC","SVC+isotonic","SVC+sigmoid"]
svc = SVC(kernel = "linear",gamma=1)
models_svc = [svc
             ,CalibratedClassifierCV(svc, cv=2, method='isotonic')
             ,CalibratedClassifierCV(svc, cv=2, method='sigmoid')]
for clf, name in zip(models_svc,name_svc):
    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    if hasattr(clf, "predict_proba"):
        prob_pos = clf.predict_proba(Xtest)[:, 1]
    else:
        prob_pos = clf.decision_function(Xtest)
        prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
    clf_score = brier_score_loss(Ytest, prob_pos, pos_label=y.max())
    score = clf.score(Xtest,Ytest)
    print("{}:".format(name))
    print("\tBrier:{:.4f}".format(clf_score))
    print("\tAccuracy:{:.4f}".format(score))