leetcode算法题基础（四十二） 回溯算法总结

前言

回溯法，⼀般可以解决如下⼏种问题：

• 组合问题：N个数⾥⾯按⼀定规则找出k个数的集合
• 切割问题：⼀个字符串按⼀定规则有⼏种切割⽅式
• ⼦集问题：⼀个N个数的集合⾥有多少符合条件的⼦集
• 排列问题：N个数按⼀定规则全排列，有⼏种排列⽅式
• 棋盘问题：N皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序

回溯法⼀般是在集合中递归搜索，集合的⼤⼩构成了树的宽度，递归的深度构成的树的深度。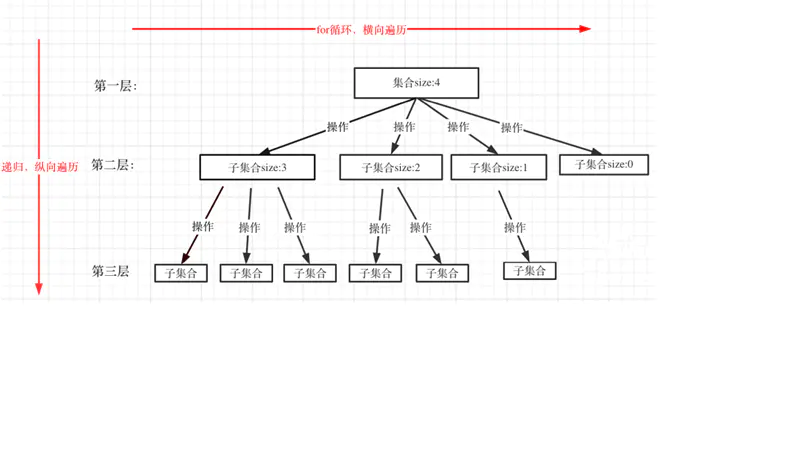

 

 回溯算法模板框架如下：

void backtracking(参数) {
 if (终⽌条件) {
 存放结果;
 return;
 }
 for (选择：本层集合中元素（树中节点孩⼦的数量就是集合的⼤⼩）) {
 处理节点;
 backtracking(路径，选择列表); // 递归
 回溯，撤销处理结果
 }
}

组合问题

组合
题⽬链接：https://leetcode-cn.com/problems/combinations/
给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输⼊: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

思路

把组合问题抽象为如下树形结构：

 

 

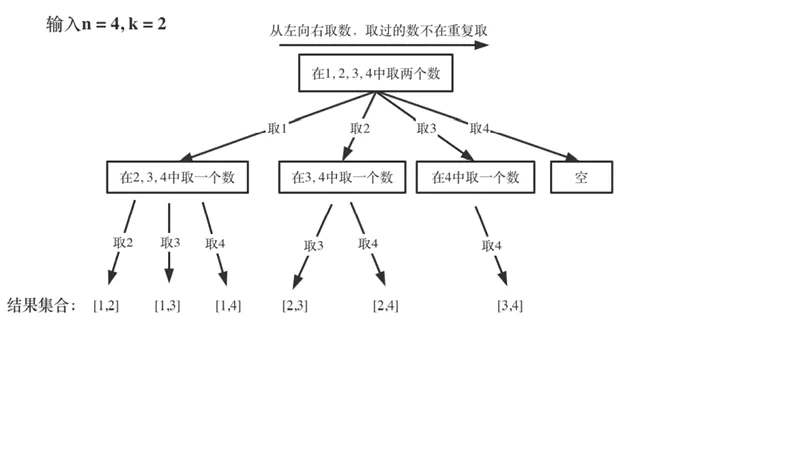
可以看出这个棵树，⼀开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。
第⼀次取1，集合变为2，3，4 ，因为k为2，我们只需要再取⼀个数就可以了，分别取2，3，4，得到集
合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进⾏⽽收缩，调整可选择的范围
图中可以发现n相当于树的宽度，k相当于树的深度

那么如何在这个树上遍历，然后收集到我们要的结果集呢？
图中每次搜索到了叶⼦节点，我们就找到了⼀个结果。
相当于只需要把达到叶⼦节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

---

组合问题如何进⾏剪枝?

举⼀个例⼦，n = 4，k = 4的话，那么第⼀层for循环的时候，从元素2开始的遍历都没有意义了。 在第⼆层for循环，从元素3开始的遍历都没有意义了。

 

 

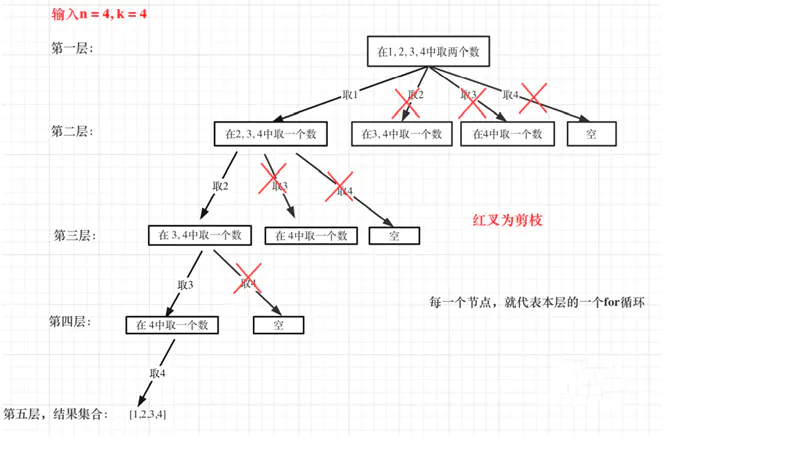
所以，可以剪枝的地⽅就在递归中每⼀层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不⾜ 我们需要的元素个数了，那么就没有必要搜索了。

一般遍历的代码如下

for (int i = startIndex; i <= n; i++) {
    dfs(下一层)
}

下一层的startindex怎么取?
一般都需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？
如果是⼀个集合来求组合的话，就需要startIndex，例如：回溯算法：求组合问题！，回
溯算法：求组合总和！。
如果是多个集合取组合，各个集合之间相互不影响，那么就不⽤startIndex，例如：回溯算法：电话号码的字⺟组合

此外,在求和问题中，排序之后加剪枝是常⻅的套路

---

去重问题

都知道组合问题可以抽象为树形结构，那么“使⽤过”在这个树形结构上是有两个维度的，⼀个维度是同⼀树枝上使⽤过，⼀个维度是同⼀树层上使⽤过。没有理解这两个层⾯上的“使⽤过” 是造成⼤家没有彻底理解去重的根本原因。

如元素在同⼀个组合内是可以重复的，怎么重复都没事，但两个组合不能相同
所以我们要去重的是同⼀树层上的“使⽤过”，同⼀树枝上的都是⼀个组合⾥的元素，不⽤去重

强调⼀下，树层去重的话，需要对数组排序！

来举⼀个例⼦，candidates = [1, 1, 2], target = 3，（⽅便起⻅candidates已经排序
了）

选择过程树形结构如图所示：

 

 

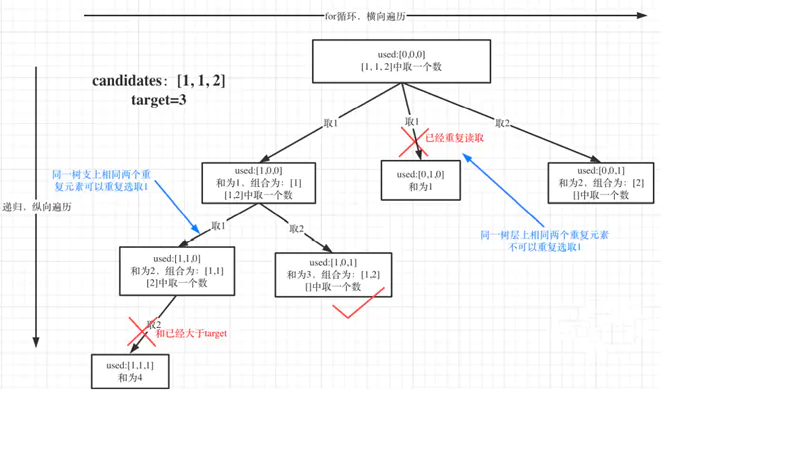
如果 candidates[i] == candidates[i - 1] 并且 used[i - 1] == false ，就说明：前⼀个树枝，使⽤了candidates[i - 1]，也就是说同⼀树层使⽤过candidates[i - 1]。

此时for循环⾥就应该做continue的操作。
这块⽐较抽象，如图：

 

 

去重2.png

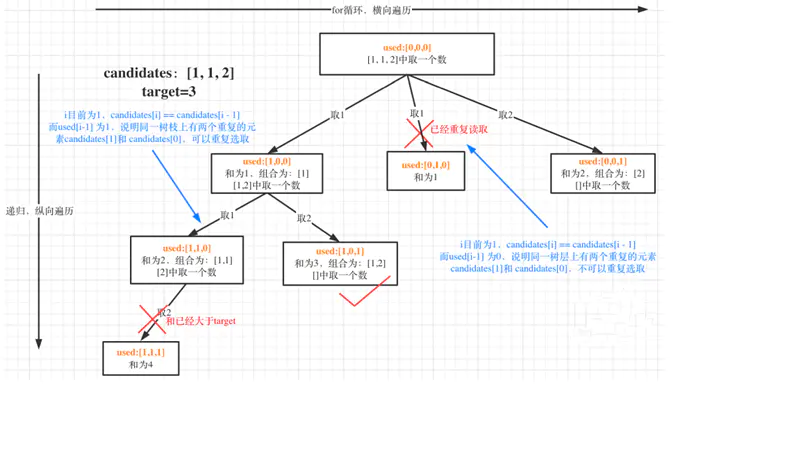
我在图中将used的变化⽤橘⻩⾊标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

• used[i - 1] == true，说明同⼀树⽀candidates[i - 1]使⽤过
• used[i - 1] == false，说明同⼀树层candidates[i - 1]使⽤过

作者：知止9528
链接：https://www.jianshu.com/p/8fc2257d1f4e
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。