李航统计学习方法(第二版)基本概念（二）：统计学习的分类

1 基本分类

1.1.监督学习

输入空间(input space )：输入所有可能取值的集合

输出空间(output space)：输出所有可能取值的集合，通常输出空间远远小于输入空间

特征空间：每个具体的输入是一个实例(instance)，通常由特征向量(feature vector)表示。这时，特征向量存在的空间称为特征空间 (feature space)

符号：

 

 

 联合概率分布：

监督学习假设输入与输出的随机变量X和Y遵循联合概率分布P(X, Y).P(X, Y)表示分布函数，或分布密度函数。
假设空间：

监督学习的目的在于学习一个由输入到输出的映射，这一映射由模型来表示。模型属于由输入空间到输出空问的映射的集合，这个集合就是假设空间

问题的形式化：

 

 

 

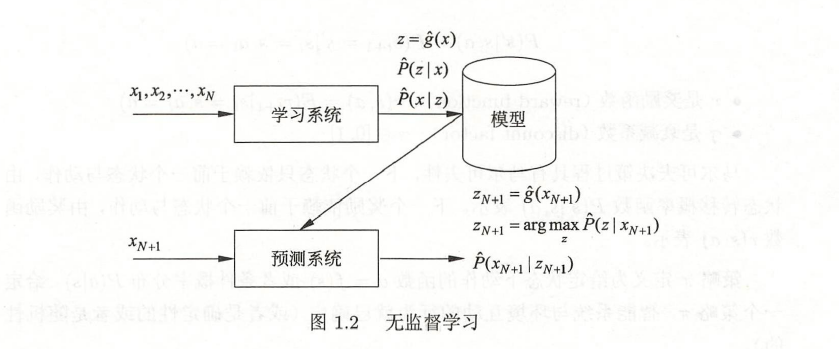
1.2.无监督学习

无监督学习(unsupervised learning)：

是指从无标注数据中学习预测模型的机器学习问题。

无标注数据是自然得到的数据，预测模型表示数据的类别、转换或概率。

每一个输出是对输入的分析结果，由输入的类别、转换或概率表示。如聚类、降维或概率估计。

 

 

 问题的形式化：

 

 

 

 

 

 

1.3 强化学习

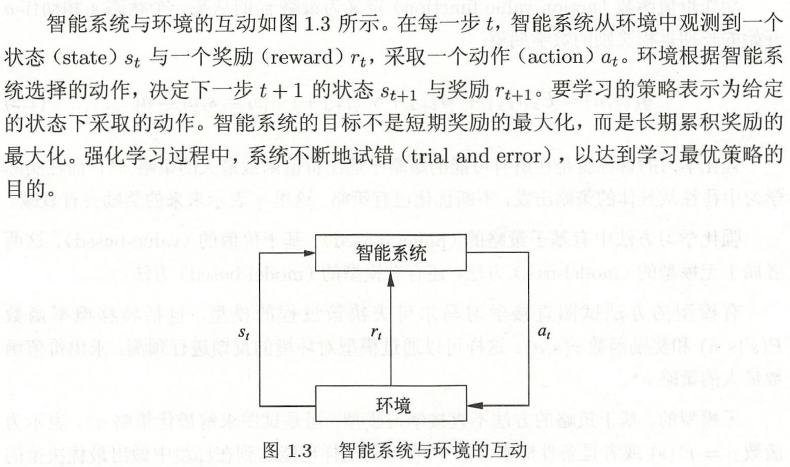
强化学习(reinforcement learning)是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。

智能系统与环境

 

概念公式

 

 

 

价值函数与动作价值函数

 

 

1.4 半监督学习与主动学习

2 按模型分类

2.1 概率模型

监督学习：取条件概率分布形式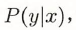：  ,x是输入，y是输出

 

 

非监督学习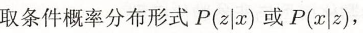：x是输入，z是输出

例如：决策树、朴索贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型是概率模型

2.2 非概率模型

监督学习：取函数形式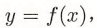：,x是输入，y是输出

 

 

非监督学习：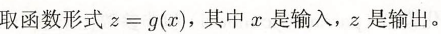

 

 例如：感知机、支持向量机、k近邻、AdaBoost, k均值、潜在语义分析，以及神经网络

逻辑斯谛回归既可看作是概率模型，又可看作是非概率模型。

2.3 概率模型与非概率模型区别 

概率模型和非概率模型的区别不在于输入与输出之间的映射关系，而在于模型的内在结构。

概率模型一定可以表示为联合概率分布的形式，其中的变量表示输入、输出、隐变量甚至参数。而针对非概率模型则不一定存在这样的联合概率分布。

2.4 线性模型与非线性模型

如果函数是线性函数，则称模型是线性模型，否则称模型是非线性模型。

2.5 参数化模型与非参数化模型

参数化模型：假设模型参数的维度固定，模型可以由有限维参数完全刻画

非参数化模型：假设模型参数的维度不固定或者说无穷大，随着训练数据量的增加而不断增大。

参数化模型适合问题简单的情况，现实中问题往往比较复杂，非参数化模型更加有效。

3 按算法分类

3.1 在线学习

在线学习是指每次接受一个样本，进行预测，之后学习模型，并不断重复该操作的机器学习。

在线学习表现

3.2 批量学习

批量学习一次接受所有数据，学习模型，之后进行预测

4 按技巧分类

4.1 贝叶斯学习

贝叶斯定理：

后验概率：计算在给定数据条件下模型的条件概率，即后验概率

4.2 核方法

核方法(kernel method)是使)i3核函数表示和学习非线性模型的一种机器学习方法，可以用于监督学习和无监督学习。

把线性模型扩展到非线性模烈，直接的做法是显式地定义从输入空间(低维空间)到特征空间(高维空间)的映射，在特征空间中进行内积计算。