李航统计学习方法(第二版)(十三):线性可分支持向量机与硬间隔最大化
1 简介
支持向量机(support vector machines> SVM)是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;支持
向量机还包括核技巧,这使它成为实质卜的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming)的
问题,也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。
当训练数据线性可分时,通过硬间隔最大化(hard marlin maximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机
2 模型
2.1 相关条件

2.2 模型定义

3 学习策略
3.1 相关概念
3.1.1 函数间隔

3.1.2 几何间隔

3.1.3 函数间隔与几何间隔的关系

3.1.4 硬间隔最大化
对线性可分的训练数据集而言,线性可分分离超平面有无穷多个(等价于感知机),但是几何间隔最大的分离超平面是唯一的。这里的间隔最大化又称为硬间隔最大化。
间隔最大化的直观解释是:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。也就是说,不仅将能将正负实例点分开,而且对最难
分的实例点(离超平面最近的点)也有足够大的确信度将它们分开。这样的超平面应该对未知的新实例有很好的分类预测能力。
3.2 凸优化

3.3 最终策略

4 算法
4.1 普通形式


4.2 对偶形式

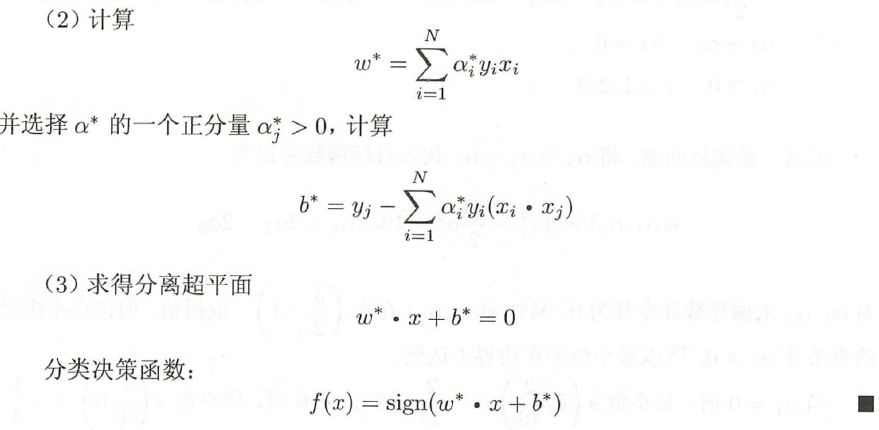
本文来自博客园,作者:秋华,转载请注明原文链接:https://www.cnblogs.com/qiu-hua/p/12801016.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号