模拟法与螺旋矩阵

模拟法与螺旋矩阵

模拟法，就像其字面意思一样，使用计算机程序去模拟一个实际的过程。其实常见的模拟法不涉及到任何具体的算法，它只需要你的代码按照实际过程去运行。使用模拟法最重要的地方在于要分清模拟的各个过程，将一个过程分解为多个过程——方便我们去模拟，否则等着你的可能是极其复杂的边界检测。

54. 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

题目分析

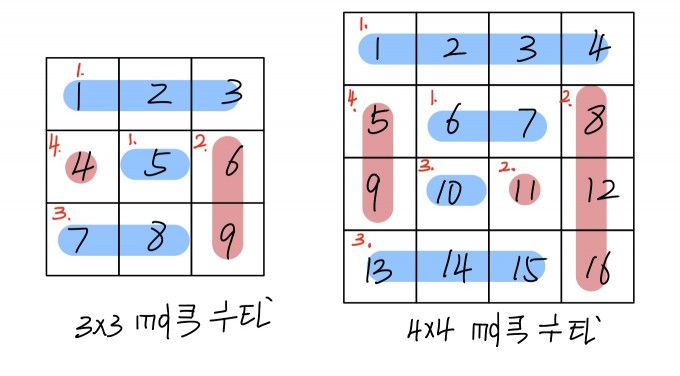
按照顺时针顺序螺旋打印一个矩阵最关键的地方在于如果模拟出“螺旋”，我们以两个简单矩阵为例，简单地分析一下：

如图所示，打印螺旋矩阵只需要四个步骤：

1. 从左至右
2. 从上至下
3. 从右至左
4. 从下至上

只需要循环执行这四个步骤就可以按顺时针提取出矩阵元素，但是这个四个步骤的边界如何确定呢？

我们设置四个动态边界量（l，r，t，b），用以标记矩阵的四个边界范围，一旦矩阵的某行或某列被遍历过，我们就更新对应的边界值，这样可以去掉被遍历过的元素。

定量地描述打印螺旋矩阵的步骤：

1. 从左至右：设置变量j从l遍历至r，此时t行被遍历过了，将其从矩阵中剔除，也就是t++

2. 检测自增后的t是否超过b，如果超过，意味着没有元素需要遍历，结束循环

3. 从上至下：设置变量i从t遍历至b，此时r列被遍历完了，将其从矩阵中剔除，也就是r--

4. 检测自减后的r是否小于l，若是则break

5. 从右至左：设置变量j从r遍历至l，此时b行被遍历完了，将其从矩阵中剔除，也就是b--

6. 检测自减后的b是否小于t，若是则break

7. 从下至上：设置变量i从b遍历至t，此时l列被遍历完了，将其从矩阵中剔除，也就是l++

8. 检测自增后的l是否超过r，若是则break

9. 重复执行以上步骤，直到某个边界检查被打破

代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> list = new ArrayList<>();
        int l = 0, r = matrix[0].length - 1, t = 0, b = matrix.length - 1;
        while (true) {
            for (int j = l; j <= r; j++)
                list.add(matrix[t][j]);
            if (++t > b)
                break;
            for (int i = t; i <= b; i++)
                list.add(matrix[i][r]);
            if (--r < l)
                break;
            for (int j = r; j >= l; j--)
                list.add(matrix[b][j]);
            if (--b < t)
                break;
            for (int i = b; i >= t; i--)
                list.add(matrix[i][l]);
            if (++l > r)
                break;
        }
        return list;
    }
    
}