习题2.12

1.代码实现

点击查看代码

import numpy as np
from sympy import Matrix, symbols

# 定义一个矩阵
A = np.array([[-1,1,0],[-4,3,0],[1,0,2]])

# 使用numpy.linalg.eig求解特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)

print("数值解的特征值：", eigenvalues)
print("数值解的特征向量：\n", eigenvectors)


# 定义符号变量（虽然在这个例子中我们不需要显式地定义它们，但SymPy内部会使用）
# x, y = symbols('x y')  # 在这个例子中不需要

# 定义一个符号矩阵
A = Matrix([[4, 2], [1, 3]])

# 使用.eigenvects()方法求解特征值和特征向量（符号解）
eigenvects = A.eigenvects()

print("符号解的特征值和特征向量：")
for lambda_, multiplicity, vectors in eigenvects:
    print(f"特征值: {lambda_}, 多重性: {multiplicity}")
    for vector in vectors:
        print(f"特征向量: {vector}")
print("学号：3014")

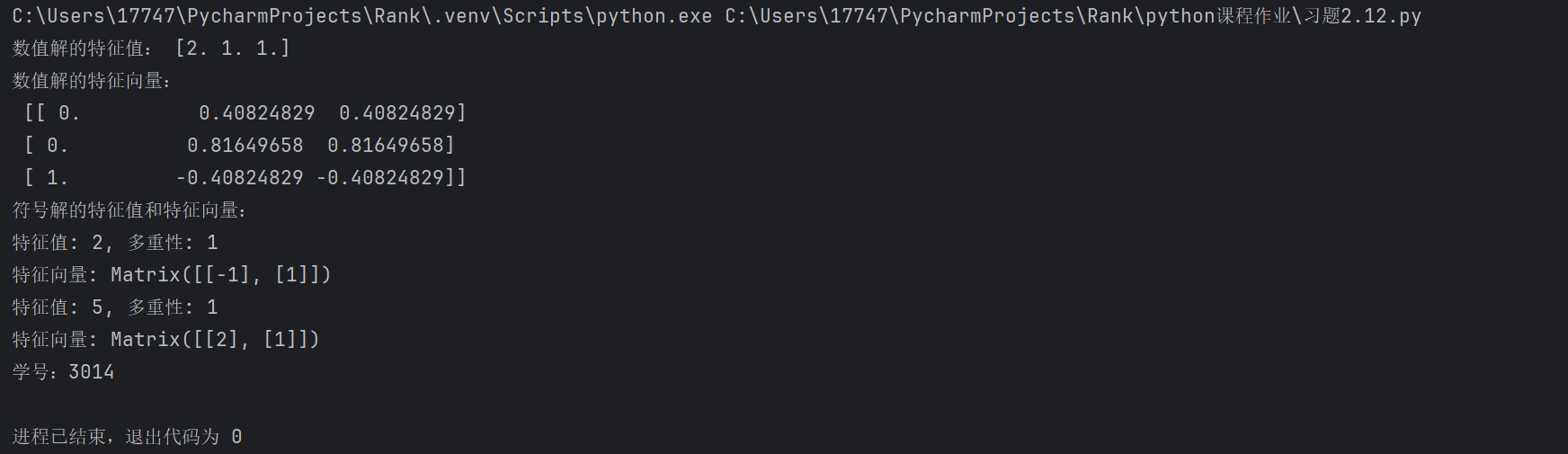
2.运行结果