Leetcode之动态规划（DP）专题-72. 编辑距离（Edit Distance）

Leetcode之动态规划（DP）专题-72. 编辑距离（Edit Distance）

---

 

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

1. 插入一个字符
2. 删除一个字符
3. 替换一个字符

示例 1:

输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2:

输入: word1 = "intention", word2 = "execution"
输出: 5
解释: 
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

---

我们定义dp[i][j]为：
截取长度为i的word1字符串 需要更改多少次才能变成 截取长度为j的字符串。
举例：
示例1中，dp[1][1]代表"h"->"r" 需要多少次？
dp[2][2]表示"ho"变成"ro"需要多少次？

我们可以写出状态转移方程：如果word1[i]==word2[j]，那么dp[i][j] = dp[i-1][j-1];
如果不相等，那么dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]);

我们画一下dp的表格

 

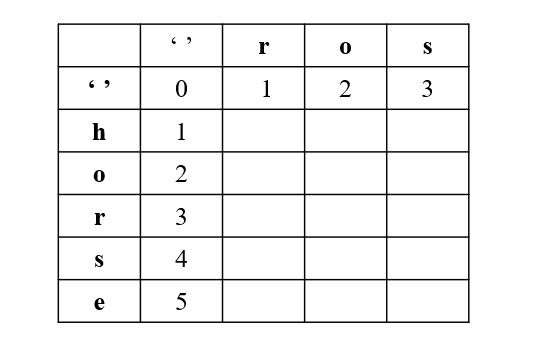
 我们分析第一行内容：

 

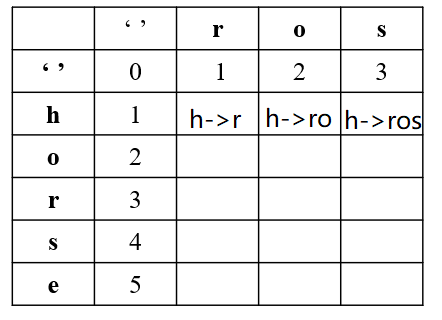
 h变成r需要1次，h->ro需要2次，h->ros需要3次。

那么这三个空填入的值分别为：1、2、3

h->ro是由h->r然后再增加一个o变成的，依次类推。

 

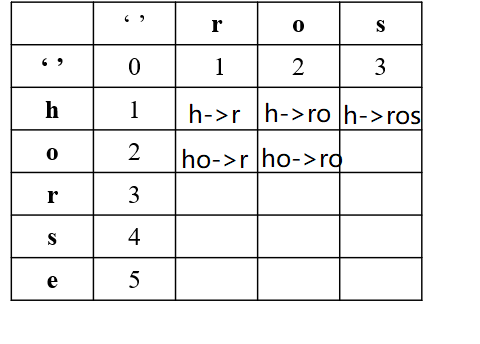
 我们再来看这一步，ho->r需要2步，ho->ro，其中第二个o是相同的，不需要更改，所以等同于h->r

 

于是，状态转移方程就分析完了：

如果word1[i]==word2[j]，那么dp[i][j] = dp[i-1][j-1];
如果不相等，那么dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]);

AC代码：

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m+1][n+1];
        for (int i = 1; i < m+1; i++) {
            dp[i][0] = dp[i-1][0]+1;
        }
        for (int i = 1; i < n+1; i++) {
            dp[0][i] = dp[0][i-1]+1;
        }
        for (int i = 1; i < m+1; i++) {
            for (int j = 1; j < n+1; j++) {
                if(word1.charAt(i-1)==word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = Math.min(Math.min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1]) + 1;
                }
            }
        }
        return dp[m][n];
    }
}