Leetcode之深度优先搜索（DFS）专题-1080. 根到叶路径上的不足节点（Insufficient Nodes in Root to Leaf Paths）

Leetcode之深度优先搜索（DFS）专题-1080. 根到叶路径上的不足节点（Insufficient Nodes in Root to Leaf Paths）

 

这篇是DFS专题的第一篇，所以我会写下具体的解题步骤和过程，以及我当时的思路，有改进的地方，希望指正，共同进步。

---

 

给定一棵二叉树的根 root，请你考虑它所有 从根到叶的路径：从根到任何叶的路径。（所谓一个叶子节点，就是一个没有子节点的节点）

假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为「不足节点」，需要被删除。

请你删除所有不足节点，并返回生成的二叉树的根。

 

示例 1：

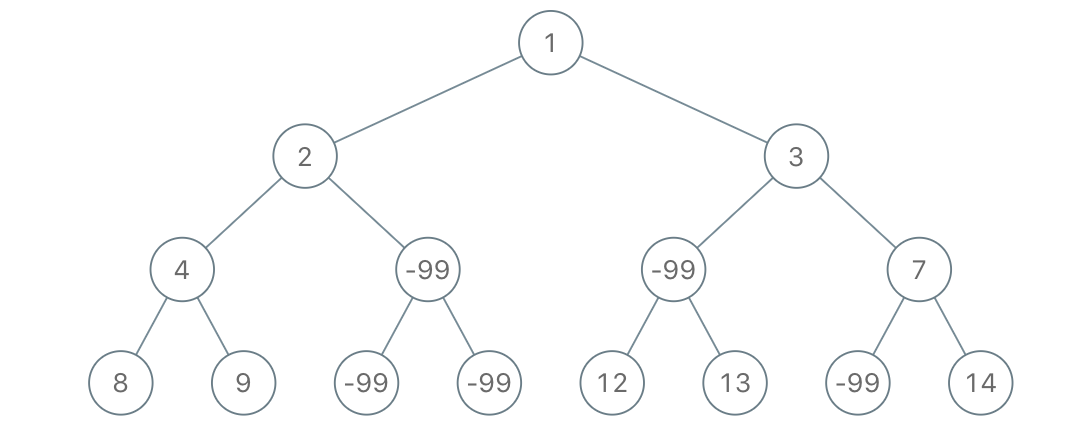
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1

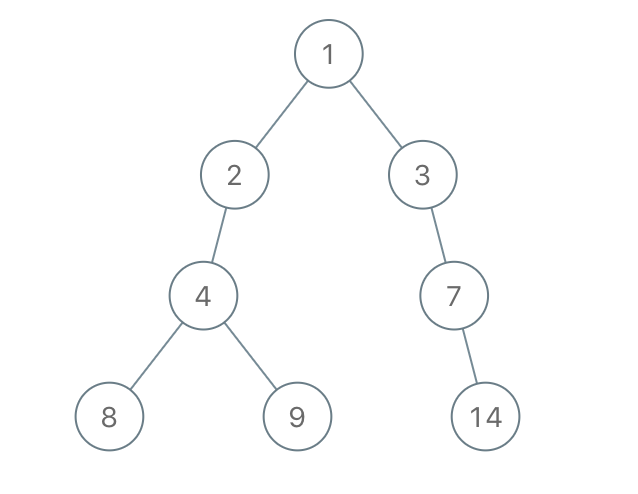
输出：[1,2,3,4,null,null,7,8,9,null,14]

 

示例 2：

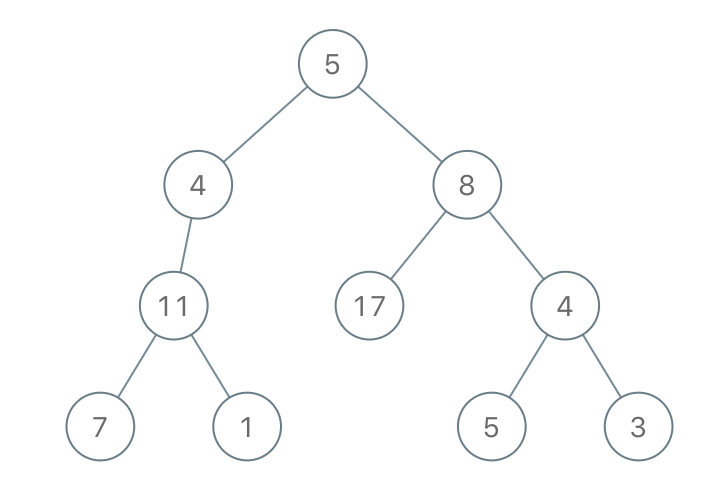
输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22

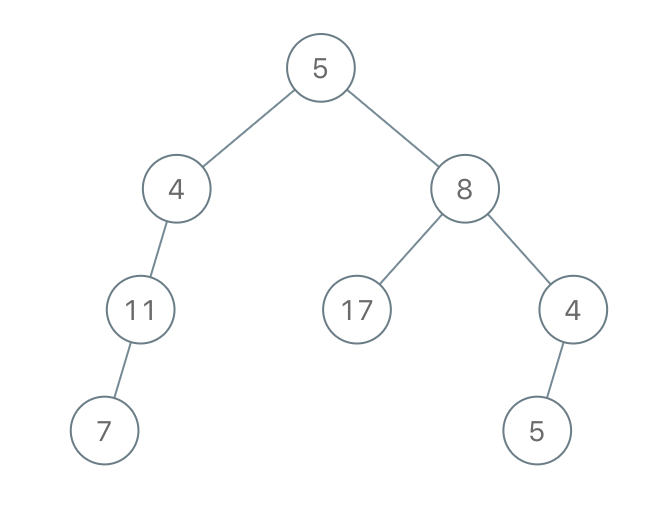
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

 

示例 3：

输入：root = [5,-6,-6], limit = 0
输出：[]

 

 

 

提示：

 

1. 给定的树有 1 到 5000 个节点
2. -10^5 <= node.val <= 10^5
3. -10^9 <= limit <= 10^9　　

　　

---

分析：

1、首先我们要确定如何删除（即删除的规则）：

　　读题，大概知道大意后，由于题意不是很清晰，我们观察样例。

　　在观察了样例1后，我大致得出结论，从根-叶子节点的这一段路程里，最后的和如果小于limit，这个叶子节点就要被删除。

　　同时，很重要一点的是，当一个节点变成叶子节点后，它也应该被删除。（观察样例1中左边的三个-99被删除的情况）

　　此时，对推断还不是很确信，再观察样例2和样例3，确定推断。

　　观察样例3时发现，当根节点失去左右儿子的时候，它自己也同时删除，那么只用返回一个null就行了。

 

2、DFS函数，确定参数个数和各个参数

　　很明显，我们这题需要去遍历一个树，当到达叶子节点时，检查sum值是否小于limit，如果小于，我们要执行删除这个过程。

　　此时，删除这个过程，我们通知它的父节点，与他断开连接。

　　那我们则需要给父节点返回一个消息，告诉父节点，需要删除与之的连接。

　　所以，我们确定了返回类型为boolean，返回true为需要删除，返回false为保留。

　　参数方面，传入一个TreeNode，一个limit值，和一个sum用于存储现在的和。

 

3、编写dfs函数

　　在dfs函数中，我们有两个变量，我把它命名为leftDeleted和rightDeleted，分别代表左节点和右节点是否删除，true表示没有左（右）儿子节点。

　　同时，遍历一个树的方法有：1、先序遍历 2、中序 3、后序

　　我们在这题中，需要得知左右儿子节点的 有无 之后，才能执行删除操作，然后再告诉这个节点的上级，它是否要被删除。

　　

　　举个例子：

　　节点1有 左儿子（称为节点2），没有右儿子。

　　节点2分别有左右儿子。

　　在这个过程中，节点2的左右儿子被删除，那么节点2变成了叶子节点，节点2也应该被删除，

　　所以节点2需要返回true给节点1，告诉节点1要删除与之的连接。

 

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sufficientSubset(TreeNode root, int limit) {
       if(root==null) return root;
       dfs(root,limit,0);
        if(root.left == null && root.right == null){
            return null;
        }
        return root;
    }
    
    public boolean dfs(TreeNode root,int limit,int now){
        if(root.left==null && root.right==null){
            if((now+root.val)<limit) return true;
            else return false;
        }
        boolean leftDeleted = false;
        boolean rightDeleted = false;
        if(root.left!=null){
            if(dfs(root.left,limit,now+root.val)){
                root.left = null;
                leftDeleted = true;
            }
        }else leftDeleted = true;
        if(root.right!=null){
            if(dfs(root.right,limit,now+root.val)){
                root.right = null;
                rightDeleted = true;
            }
        }else rightDeleted = true;
        
        if(rightDeleted && leftDeleted){
            return true;
        }
        return false;
    }
    
}