交叉熵的前世今生
转自:https://www.zhihu.com/question/22178202
对于确定性过程和随机性过程是理解是非常容易的,任何人都知道对于一个函数\(f(x) = 4x^2+x+2\)来说,给定\(x=2\),函数值一定为20,这是一个确定性的过程;对于抛掷硬币,是一个随机性过程,但是通过上百次的实验之后,我们知道抛掷结果为正面的概率为0.5,但是实验过程是不确定的。
不确定性在自然中广泛的存在,如何使用数学语言来刻画?熵就是关于不确定性的一个极好的数学描述。历史上的熵概念起源于热力学。
1. 信息熵
1948年,在贝尔实验室里研究通讯技术的电子工程师克劳德·香农(1916-2001)发表一篇论文,通讯的数学理论,引进了“信息熵的概念,开启了现代信息论研究的先河。最初,香农并没有称他关于信息传输中不确定性的度量化。他甚至都不太知晓所考虑的量和热力学熵之间的相似性,曾称之“information”,“uncertainty”;后来在数学家冯诺依曼的指引下,最终称为熵。
香农的信息熵的本质是不确定现象的数学化度量,对于一般的不确定事件,我们怎样刻画它的不确定程度呢?假设有n个基本事件,每个事件发生的概率为\(p_1,p_2,..,p_n\),他们构成一个样本空间,也称为概率数组。例如投掷硬币,它包含的基本事件为硬币正面朝上和硬币反面朝上,并且每个事件的概率为0.5,则样本空间为{0.5,0.5}。我们记一个样本空间的不确定度为H,对于投掷硬币,则不确定度为H(0.5,0.5)。
性质1:基本不等式 更一般来说,使用\(H(p_1,p_2,...,p_n)\)记为样本空间\((p_1,p_2,...,p_n)\)所对应的不确定度。运用直觉分析,如果所有基本事件的机会均等,即所有事件具有同样的概率\(1/n\),其不确定性最大。则有基本不等式:
性质2:单调性 此外,投掷骰子的样本空间为\(H(\frac 16,\frac 16,\frac 16,\frac 16,\frac 16,\frac 16)\),投掷硬币的样本空间为\(h(0.5,0.5)\)。同样采用直觉分析,对于基本事件均等的样本空间,随着基本事件的数量,其不确定性就越大。
性质3:加权和 ,如果一个不确定时间被分解成几个持续时间,则原先时间的不确定度等于持续时间的不确定度的加权和。例: \(H(\frac 12,\frac 13,\frac 16) = H(\frac 12,\frac 12) + \frac 12H(\frac 23,\frac13)\)
性质4: 对于固定的自然数n,不确定度函数H是一个连续函数。
香农证明了,任何在所有样本空间上都有定义的函数H,只要满足上面的性质(2),(3),(4),都有:
按照冯诺依曼的建议,这个函数被定义为样本空间\((p_1,p_2,...,p_n)\)所对应的信息熵,现在,这个被称为是“香农熵",以纪念信息论之父香农。
2.证明信息熵
第一步(证明等概率时成立):
将\(H(\frac 1n,...,\frac 1n)\)记为\(A(n)\),设n = 8,根据性质三,可以证明\(A(2^3) = 3A(2)\).
使用数学归纳法,可以得:\(A(s^m) = mA(s)\),(a)
假设四个正整数\(t,s,n,m\)满足下面不等式,\(s^m \le t^n \le s^ {m+1}\),可得\(\frac mn \le \frac {ln t}{ln s} \le \frac {m+1}n\),可得\(|\frac mn-\frac {ln~t} {ln~s}| < \frac 1n\).(b)
由性质2,可知\(A(k)\)是k的递增函数,故由(a)可推出\(mA(s) \le nA(t) \le (m+1)A(s)\),可得\(|\frac mn - \frac {A(t)}{A(s)}| \le \frac 1n\)(c).
由(b),(c)可得:
\(|\frac{A(t)}{A(s)} - \frac {ln~t}{ln~s}| \le \frac 2n\)
因为n是任意的,则\(\frac {A(t)}{A(s)} = \frac {ln~t}{ln~s}\)
故存在常数C使得所有正整数t,都有\(A(t) = Cln~t= ln~t\),因此
,即公式在\(p_1,p_2,..,p_n = \frac 1n\)时成立。
第二步(证明对所有和为1的正有理数\(p_i\)成立):
假设一个样本空间为{\(\frac 12,\frac 13,\frac 16\)},根据性质3,可以分解为:
假设成有理数的分数形式:
则\(H(p_1,p_2,p_3)\)可以分解为:
将{\(p_1,p_2,p_3\)}推广到一般情况,设样本空间为{\(p_1,p_2,...,p_k\)},其中\(p_i = \frac {n_i}{n_1+n_2+...+n_k},其中,i= 1,2,...,k\)则可改写为:
将第一步中得到的结论(\(A(n) = ln~n\))带入:
第三步(证明对于所有和为1的非负实数成立):
既然信息熵的公式H对于所有和为1的所有有理数成立,有性质4连续性条件,可以推出它对所有和为1的非负实数成立。
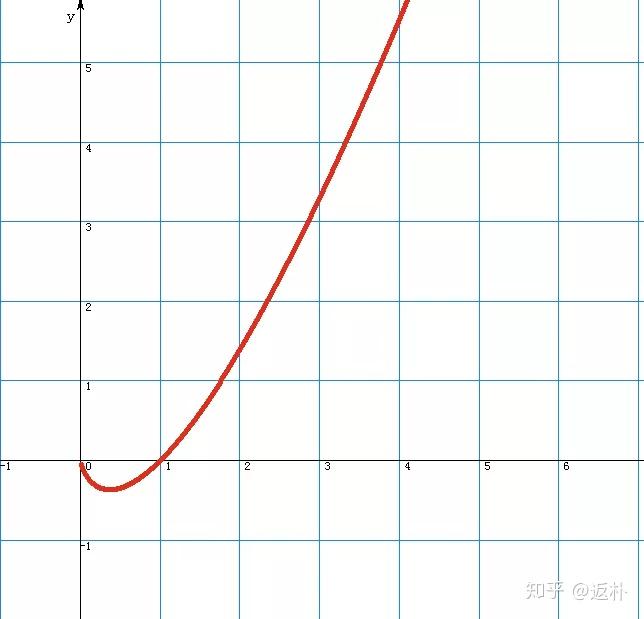
上图为函数\(f(x) = xln~x\)的函数图像,对于信息熵公式,除了负号,可以看作是有限个f(x)函数值之和。这个函数的图像像一个勺子,根据向上弯曲的几何性质:连接函数上任意两点的直线段都在这两点之间的曲线段之上,运用初等微分学,可以证明,对于任意两个正数a和b,都有:
这就是吉布斯不等式,当样本空间中的所有概率值都为\(\frac 1n\)时,吉布斯熵就还原成玻尔兹曼熵,他是最大可能的吉布斯熵,信息熵的最大值等于ln n。
3. 柯尔莫果洛夫熵
俄罗斯数学巨人柯尔莫果洛夫(1903-1987),不仅在数学界颇有成就,其指导的学生也大有作为。
回到投掷硬币的例子中,这一次我们不止注意一次的结果,而是一次投掷好几次看看有多少种可能发生。假设连续投掷两次,可能出现的结果有四种:正正,正反,反正,反反。因为第一次投掷硬币对第二次毫无影响,他们都是相互独立的,因而四种结果的每一次可能性都是四分之一。为了简化书写,记H表示正面朝上,T表示反面朝上,这样所有的可能性为:TT,TF,FT,FF。对于连续投掷n个隐蔽,一共有2n个可能的结果,每一个结果的概率为\(\frac 1{2^n}\),每个结果都是一个基本事件,此时就有一个包含2^n个基本事件的样本空间{\(\frac 1{2^n},...,\frac 1{2^n}\)},熵值为\(n ln~2\)
那么问题来了,无论抛了多少次,对下一次的结果仍然是一个未知数。一个极端的例子,加入投掷了一百万次都是头像朝上,第一百万零一次?柯尔莫果洛夫对下面的问题产生了兴趣,倘若已知来连续抛出n次硬币的结果,接下来抛第n+1次的结果的不确定度到底时多少?
我们进一步简化标签,采用0代表H,1代表T,对于连续n次抛硬币的结果可以用小数\(0.a_1a_2...a_n\)来表示,其中小数部分由0和1组成,假设这是一个二进制小数,则可以改写为:
现在将区间【0,1】一分为二,左边的半个区间【0,0.5),右边的半个区间【0.5,1】。这两个区间的交集是空集,没有共同元素。如果a1为0,则x输入【0,0.5);如果a1为1,则x输入【0.5,1】。如果a1= 1,a2已知,如果确定x的位置呢?
我们可以将【0,1】区间映射到自身熵一个逐段线性的“加倍函数”来解释连续投掷硬币的数学游戏,这个函数的定义是:当x大于或等于0并且小于1/2时函数值为2x,当x大于或等于1/2并小于或等于1时函数值为2x - 1.简单来说,这个函数就是将自变量加倍,在丢掉结果的整数部分,简洁的表达式为\(f(x) = 2x (mod~1)\),其函数的图像时两条斜率为2,彼此平行的斜的整数部分。它们时保持长度的,也就是说,任何子区间和它的f下的逆像都有相同的长度。一个区间在函数下的逆像时函数定义域中所有数的全体。加倍该函数并不是处处来连续的,在区间的中点处,有一个跃度为1的跳跃间断点。
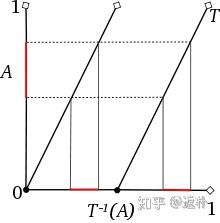
这个函数的赋值都离不开乘2。事实上,由二进制数的展开式容易看出,当x写成二进制数\(0.a_1a_2...a_n\)可以转化为\(f(x) = 0.a_1a_2...a_n = \frac {a_1}2 + \frac {a_2}{2^2} + ... + \frac {a_n}{2^n}\),因此,a2等于0隐含这x属于【0,0.5),a2等于1意味着x输入【0.5,1】。一般说来,若x的第i个数字\(a_i = 0\),则x的第i-1个迭代点\(f_{i-1}\)输入【0,0.5),若\(a_i=1\),则x的第i-1个迭代点\(f_{i-1}\)属于【0.5,1】。这样,连续抛硬币的结果就可由点列\(x,f(x),f^2(x),...\)在区间【0,1】上划分【0.0.5)和【0.5,1】中的地址来代表。例如结果TTHTHTTT,,对应的数x = 0.11010111,所以x位于【0.5,1】,f(x)位于【0.5,1】,\(f^2(x),f^3(x),...\)
如上所知,连续投掷n次硬币的结果等价于知道前n个点\(x,f(x),f^2(x),...,f^{n-}1(x)\)在划分【0,0.5),【0.5,1】中的位置,而第n+1次是h还是T等于\(f^n(x)\)落于哪一个区间中。于是,柯尔莫果洛夫把连续抛硬币结果的不确定度问题归结于关于加倍函数f的迭代点位置的不确定问题。
进而提出,如果已知\(x,f(x),f^2(x),...,f^{n-}1(x)\)在区间【0,1】的划分p{【0,0.5),【0.5,1】}中的位置,\(f^n(x)\)在同一划分中的位置的不确定度是多少?下面论文中提供了详细的分析计算过程。
“Entropy - an introduction,” Jiu Ding and Tien-Yien Li, NankaiSeries in Pure and Applied Mathematics and Theoretical Physics, Volume 4, WorldScientific, 26-53, 1993.
动力系统寻找的是过程的终极行为,当自然数n走向无穷大时,上述不确定度的极限值就被称为函数f关于划分P的熵,这个熵值依赖于函数定义域区间【0,1】的划分。该定义域可以被划分为任意有限个彼此之间互不相交的子集,而不同的划分一般给出不同的熵值。定义域的所有规划所对应的熵的最大值就叫做f的柯尔莫果洛夫熵,也称为测量熵或者度量熵,因为它用的是勒贝格所开创的一般测度论工具来度量保测函数迭代最终性态的混乱程度。
对于投掷硬币的游戏,这个加倍函数的度量熵等于ln 2,同法可知,投掷骰子的度量熵是将自变量增加6倍后在丢掉结果整数部分的六倍函数,图像是六根斜率为6的平行线,测量度ln 6,此外还有10倍函数的熵是ln 10,百倍函数ln 100。由此可知,倍数越高,熵值越大,不确定度越大。
并没有看懂这个熵的意思。
4 玻尔兹曼熵
玻尔兹曼熵可以看成是离散形式的香农熵在连续形式下的对等物。对于有限样本空间{\(p_1,p_2,...,p_n\)},香农熵为:
也看不懂这是什么内容。
以下内容来自https://blog.csdn.net/qq_36931982/article/details/82998081
5. 相对熵
相对熵,也被称为KL散度,用来描述量化总概率分布P和Q差异的一种方法。

上图中p(x)和q(x)描述同一个问题,但是这两个描述之间存在差别。则在离散和连续随机变量的情形下,相对熵可以定义为:
利用KL散度,可以用来约束模型输出数据的概率分布。相对熵的值越小,表示Q(x)和P(x)的分布就越接近,其中Q(x)常常是预测分布,P(x)表示真实分布。
相对熵是一个事件不同分布情况差异的估计,在实际运用中如果一种分布为正确分布,另一种分布为我们训练得到的分布,则可以使用相对熵作为目标函数进行优化。
6. 交叉熵
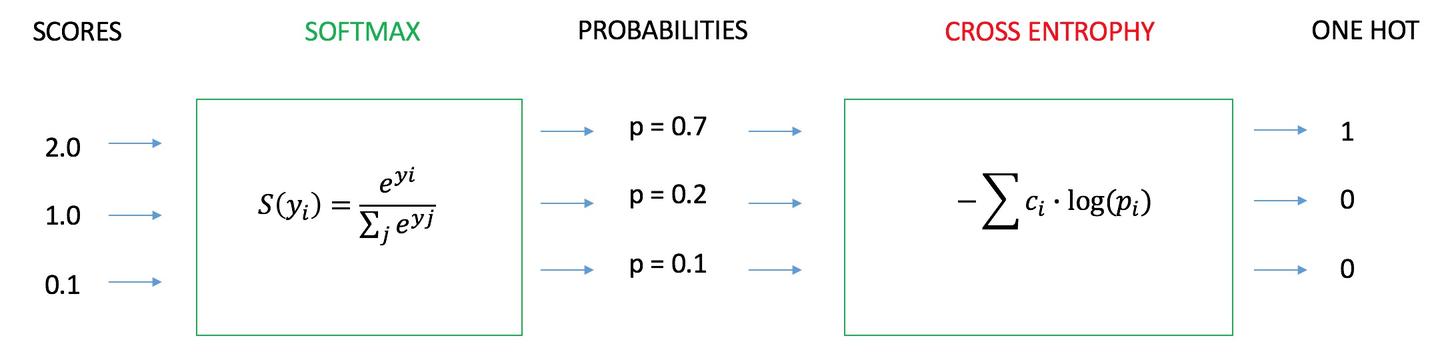
交叉熵主要度量两个概率分布间的差异性信息。
交叉熵是相对熵化简得到的:
以下内容来自https://zhuanlan.zhihu.com/p/35709485
7. 交叉熵计算实例
模型一的预测结果:
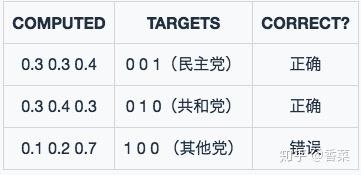
模型二的预测结果:
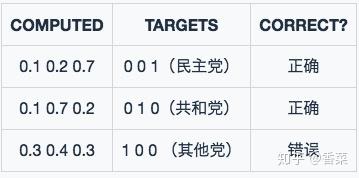
采用分类错误率来构造损失函数:
从两个模型预测出来的computed数值可以发现,model2的效果比model1的效果要好,对于识别正确的数据概率高,对于识别错误的数据概率低。
采用均方误差作为损失函数:
通过计算发现,通过mse的方式计算损失,模型2的效果比模型1的效果要好,符合真实情况。但是在梯度下降法学系时,模型学习的速度会非常的缓慢。
采用交叉熵作为损失函数:
在二分类的任务中,模型最后需要预测的结果主要有两种情况,对于每个类别预测的概率为p和1-p。则样本空间为p和1-p。
对于多分类任务,实际上是对二分类的扩展,样本空间为{\(p_1,p_2,...,p_m\)}
上面例子的计算:



