归并排序(归并排序求逆序对数)--16--归并排序--Leetcode面试题51.数组中的逆序对

面试题51. 数组中的逆序对

 　　在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

 

归并排序简介：

　　　　归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

　　将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并(如下图)。

　　归并排序时间复杂度为NlogN,仅次于快速排序(点击链接可看我之前发过的快排博文)，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

　　　　　　　　　　　　　　　　　　

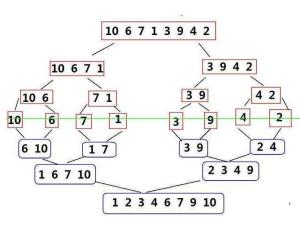
归并排序举例：

　　　　如设有数列{6，202，100，301，38，8，1}

　　　　初始状态：6,202,100,301,38,8，1

　　　　第一次归并后：{6,202},{100,301},{8,38},{1}，比较次数：3；

　　　　第二次归并后：{6,100,202,301}，{1,8,38}，比较次数：4；

　　　　第三次归并后：{1,6,8,38,100,202,301},比较次数：4；

　　　　总的比较次数为：3+4+4=11；

　　　　逆序对数为14对；

归并排序求逆序对数：具体思路是，在归并的过程中计算每个小区间的逆序对数，进而计算出大区间的逆序对数（也可以用 树状数组来求解）

代码解析：

class Solution {
    //归并排序：
    int reversepairs = 0;//逆序对数
    public int[] mergeSort(int[] nums, int left, int right){//归并排序函数
        if (left == right)//如果左边界等于右边界，说明数组只有一个值，不用排序
            return new int[] { nums[left] };
        int mid =  (right + left) / 2;//将数组分为两半

        int[] leftArr = mergeSort(nums, left, mid); //左有序数组
        int[] rightArr = mergeSort(nums, mid + 1, right); //右有序数组
        int[] newNum = new int[leftArr.length + rightArr.length]; //新的有序数组

        int m = 0, i = 0, j = 0; 
        //挨着挨着比较从左右两边的排好序的数组中从头开始比较，谁小就先放谁进新的有序空数组
        while (i < leftArr.length && j < rightArr.length){//直到左右两个有序数组有一个的遍历下标超出该数组的序列尾部
            if(leftArr[i] <= rightArr[j])//左序列的元素小，就把左序列的该元素放入新的空的有序数组中
                newNum[m++] = leftArr[i++];
            else{//右序列的元素小，就把右序列的该元素放入新的空的有序数组中
                newNum[m++] = rightArr[j++];
                reversepairs += leftArr.length - i;//左边序列数组中还有leftArr.length-i个元素大于rightArr[j],所以这也是该区间的逆序对数35             }
        }
        while (i < leftArr.length)//如果左序列的元素还有剩余的元素没放进新的空数组中，就把左序列剩余元素放入新的空的有序数组中
            newNum[m++] = leftArr[i++];
        while (j < rightArr.length)//如果右序列的元素还有剩余的元素没放进新的空数组中，就把右序列剩余元素放入新的空的有序数组中
            newNum[m++] = rightArr[j++];
        return newNum;
    }
    public int reversePairs(int[] nums) {//入口函数
        if(nums.length == 0)//如果给定的是个空数组，据题意返回0
            return 0;
        int[] newNums = mergeSort(nums, 0, nums.length - 1);//调用归并排序函数，返回一个有序的数组
        return reversepairs;//返回逆序对数
    }
}