正负数的源码 反码 补码 转
首先提几个概念: 原码,反码,补码
原码是什么?
原码就是早期用来表示数字的一种方式: 一个正数,转换为二进制位就是这个正数的原码。负数的绝对值转换成二进制位然后在高位补1就是这个负数的原码
举例说明:
int类型的 3 的原码是 11B(B表示二进制位), 在32位机器上占四个字节,那么高位补零就得:
00000000 00000000 00000000 00000011
int类型的 -3 的绝对值的二进制位就是上面的 11B 展开后高位补零就得:
10000000 00000000 00000000 00000011
但是原码有几个缺点,零分两种 +0 和 -0 。很奇怪是吧!还有,在进行不同符号的加法运算或者同符号的减法运算的时候,不能直接判断出结果的正负。你需要将两个值的绝对值进行比较,然后进行加减操作 ,最后符号位由绝对值大的决定。于是反码就产生了。
反码是什么 ?
正数的反码就是原码,负数的反码等于原码除符号位以外所有的位取反
举例说明:
int类型的 3 的反码是
00000000 00000000 00000000 00000011
和原码一样没什么可说的
int类型的 -3 的反码是
11111111 11111111 11111111 11111100
除开符号位 所有位 取反
解决了加减运算的问题,但还是有正负零之分,然后就到补码了
补码是什么?
正数的补码与原码相同,负数的补码为 其原码除符号位外所有位取反(得到反码了),然后最低位加1.
还是举例说明:
int类型的 3 的补码是:
00000000 00000000 00000000 00000011
int类型的 -3 的补码是
11111111 11111111 1111111 11111101
就是其反码加1
最后总结一下:
正数的反码和补码都与原码相同。
负数的反码为对该数的原码除符号位外各位取反。
负数的补码为对该数的原码除符号位外各位取反,然后在最后一位加1
各自的优缺点:
原码最好理解了,但是加减法不够方便,还有两个零。。
反码稍微困难一些,解决了加减法的问题,但还是有有个零
补码理解困难,其他就没什么缺点了
喔日,说到这里,估计都晕了,举个栗子把。
5的原码是 00000000000000000000000000000101(四个字节,32位(byte))
5的原码和反码,补码都一样。
-5的原码是原码除符号位以外所有的位取反 ,10000000000000000000000000000101
-5的反码就是原码符合外取反得到反码11111111111111111111111111111010
-5的补码就是反码加一得到补码11111111111111111111111111111011
最后补充一句,负数一般用补码来计算。
用补码用来运算会更加方便 另外 符号位也要参与运算 符号位会向最高位移动 减法 就是 变向的加法
如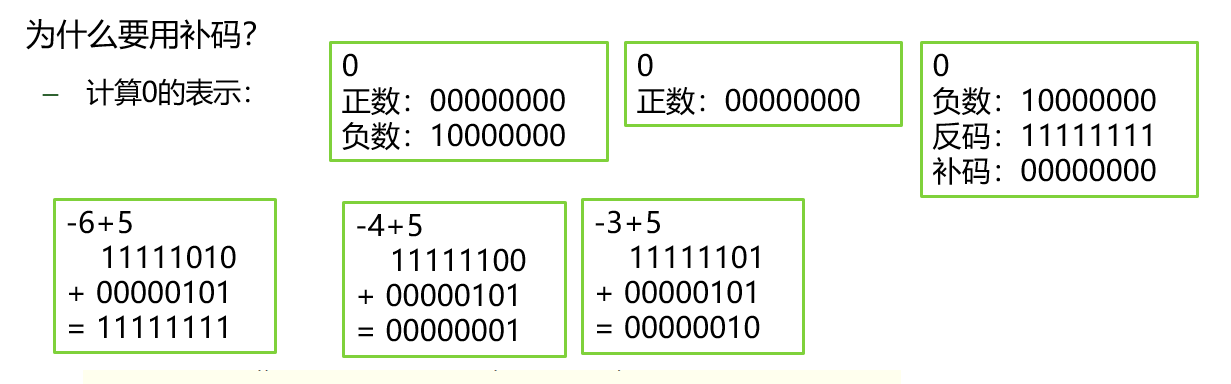
前言:随着学习计算机知识的加深,许多地方都遇到原码、反码、补码。很多关于计算机的书籍都介绍原码、反码、补码的表示方法,但是为什么要用到原码、反码、补码却没详细说。为什么要使用?它们的原理是什么呢?我搜索了许多资料,也查找了许多书籍,终于弄明白了这个问题,收集整理如下。
我们知道数值在计算机中表示形式为机器数(机器数的概念见我的另一篇日志《计算机中的原码、反码和补码》,计算机只能识别0和1,使用的是二进制。而在日常生活中人们使用的是十进制,并且我们用的数值有正负之分。于是在计算机中就用一个数的最高位存放符号(0为正,1为负)。这就是机器数的原码了。
有了数值的表示方法就可以对数进行算术运算,但是很快就发现用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下:假设字长为8bits
(1) 10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)原 + (1 0000001)原 = (1 0000010)原 = ( -2 ) 显然不正确。
因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上。对除符号位外的其余各位逐位取反就产生了反码。反码的取值空间和原码相同且一一对应。下面是反码的减法运算:
(1)10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)反 + (1 1111110)反 = (1 1111111)反 = ( -0 ) 有问题。
(1)10 - (2)10 = (1)10 + (-2)10 = (-1)10
(0 0000001)反 + (1 1111101)反 = (11111110)反 = (-1) 正确。
问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的。(印度人首先将零作为标记并放入运算之中,包含有零号的印度数学和十进制计数对人类文明的贡献极大)。
于是就引入了补码概念。负数的补码就是对反码加一,而正数的补码不变,正数的原码反码补码是一样的。在补码中用(-128)代替了(-0),这个是人为规定的,所以补码的表示范围为:
(-128~0~127)共256个。
注意:(-128)没有相对应的原码和反码, (-128) = (1 0000000) 补码的加减运算如下:
(1)10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)补 + (1 1111111)补 = (0 0000000)补 = ( 0 ) 正确。
(1)10 - (2)10 = (1)10 + (-2)10 = (-1)10
(00000001)补 + (11111110)补 = (11111111)补 = (-1) 正确。
所以补码的设计目的是:
⑴ 使符号位能与有效值部分一起参加运算,从而简化运算规则。补码机器数中的符号位,并不是强加上去的,是数据本身的自然组成部分,可以正常地参与运算。
⑵ 使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计。
所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、c等其他高级语言中使用的都是原码。
看了上面这些大家应该对原码、反码、补码有了新的认识了吧!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号