(十)T检验-第一部分
介绍T分布、T检验、Z检验与T检验、P值、相依样本以及配对样本的非独立T检验。
T分布
在到目前为止举的所有例子中,我们都假设我们知道总体参数 μ 和 σ,但很多时候,我们并不知道,我们通常只有样本,然后只能通过样本得出所有结论。
通过样本得出样本均值与总体的区别有多大?以及两个样本之间区别多大?
在所有中心值衡量指标中,我们通常使用均值,我们在此情形下要对比的两个样本可以是独立样本或非独立样本。在处理样本数据时,我们必须利用贝塞尔校正系数,根据样本标准偏差估算总体标准偏差。
通常,要看样本均值有多典型或非典型,正如之前的操作一样,我们要找到该样本均值位于样本均值分布,(即抽样分布)上的位置,如果我们知道总体参数,则可以判断该抽样分布的形状和参数,对于任何样本均值,我们都可以通过标准化找到该均值位于此分布上的位置,也就是说,算出样本均值的 Z 值,我们算出样本均值和 μ 之间的差别,然后除以标准误差,但现在标准误差取决于样本了,如果我们拥有的是样本,我们则无法再使用 σ,因此我们得出的是新的分布,该分布更容易出错,这个分布叫做 t 分布,因为它更容易出错,所以更加分散,末端比正态分布要高。
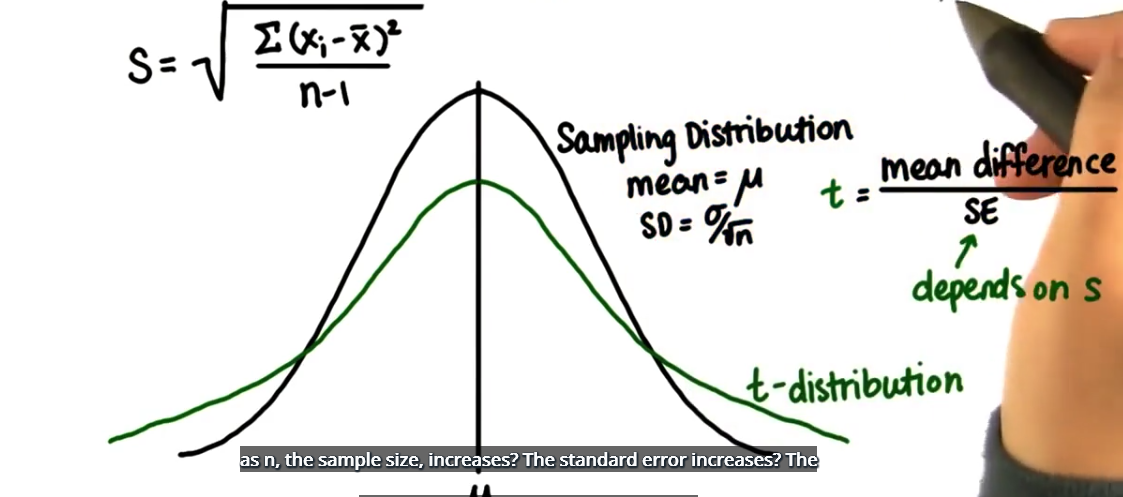
对于T分布随着样本量 n 增大,会发生什么?
A.□ 标准误差会增大
B.□ t 分布接近正态分布
C.□ t 分布的末端变得更矮(分布更窄)
D.□ 样本标准偏差 s 会更接近 σ

BCD
自由度
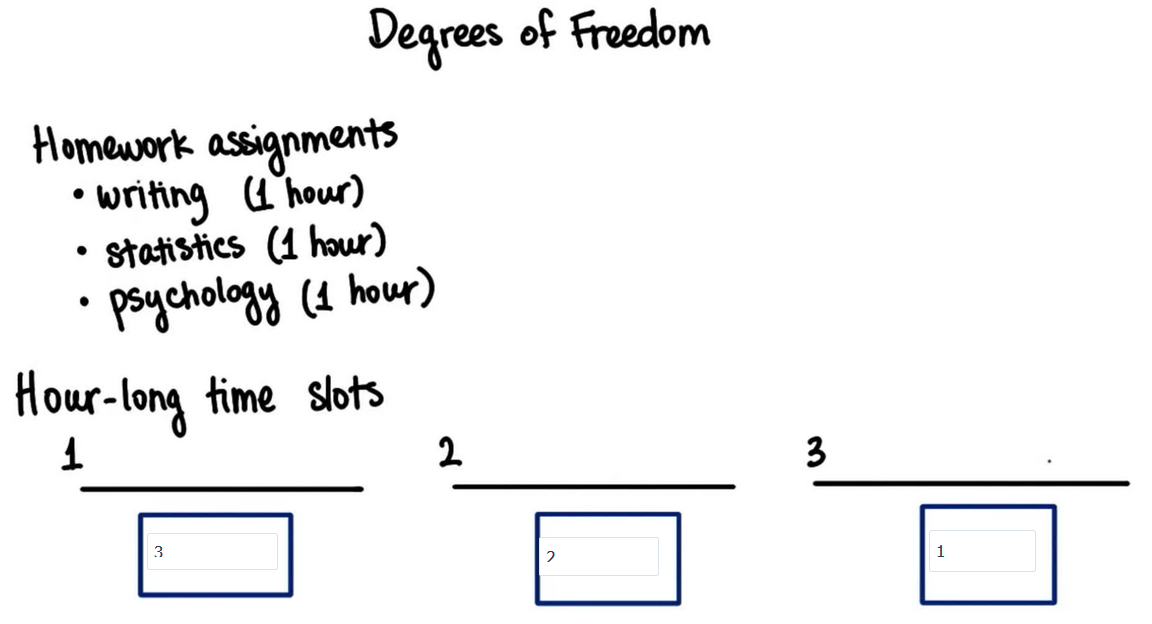
t 分布用自由度来定义,自由度很复杂,难以解释清楚,我们先讨论几个现实生活中的例子,然后再去应用这些统计概念,假设你有三道家庭作业题目要做,分别是写作、统计学和心理学,每个都将花去 1 小时,你只有 3 小时来完成它们,对于下图第一个时间空档,你可以选择写作、统计学或心理学题目,所以有 3 个选项,假设选择了写作,然后第二个空挡可以选择统计学或心理学,所以有 2 个选项,假设选择了心理学,最后一个就是定好的了,只有一个选项,即统计学。
在两个时间空档中,即第一个和第二个时间空档,你可以做出选择,你可以先做统计学题目,然后在写作和心理学题目之间选择,或者也可以先选择写作,然后在统计学和心理学之间选择等等,但是在选好前两个后,最后一个也就确定了,因此 在这个简单情形下,自由度是 2。
再来举个例子,你必须选择 n 个数字,你可以选择任何 n 个数字,n 是任何数字,可以是 5、10 或 100,你需要选择这么多的数字,这时候的自由度是多少?

n
没有限制条件规定你可以选择什么样的数字,你只需要选择 n 个数字,无论是什么数字,所以自由度是 n。
你有 n 个数字,它们的和必须是 10,即第 1 个数字加上第 2 个数字,一直加到第 n 个数字必须等于 10,你可以随意选择特定数量的值,但是这些特定数量的值之和必须等于 10,此时的自由度是多少?也就是说,你可以有多少种方式随意选择值?

自由度是 n-1 假设 n=4,即x1+x2+x3+x4 必须等于 10,我们选择一个任意的数字,我喜欢数字 13,这意味着x2+x3+x4 必须等于 10-13,即必须等于 -3,再来选择一个数字,我选择 8,到目前为止,我们选择 x1=13,x2=8,意味着 x3+x4 等于 -3-8,结果为 -11,我们还可以为 x3 或 x4 选择一个值,我选择数字 3,假设 x3=3,这意味着x4 必须等于 -11-3,结果为 -14, 所以 x4 成为固定值,但我可以选择这 3 个值,一开始有 4 个数字,自由度是 3,如果有 n 个数字,则自由度是 n-1。
再举个例子,这将非常有助于你理解自由度这一概念,你玩过九宫格游戏吗?这和九宫格游戏差不多,假设每行和每列都必须相加等于 9,你可以在这 9 个格子里填上任意的数字,只要满足这个条件就行了,所以有多少个值是可以选择的?自由度是多少?


自由度是4 A1+A2+A3=9;B1+B2+B3=9;C1+C2+C3=9;A1+B1+C1=9;A2+B2+C2=9;A3+B3+C3=9. 假设A1=5,A2=3,则A3=1; 假设B1=8,C1=-4; 假设B2=7,则C2=-1,B3=-6,C3=14; 所以我们只要知道A1,A2,B1,B2就可以知道其他字母代表的数字,所以自由度是4.

如果是 n x n 的表格,我们可以选择的值的总数量是 (n-1)^2. 在3 x 3 的表格中,我们能够选择 2 x 2 次; 在4 x 4 的表格中,我们能够选择 3 x 3 次; 在n x n 的表格中,我们能够选择 (n-1)x(n-1) 次。
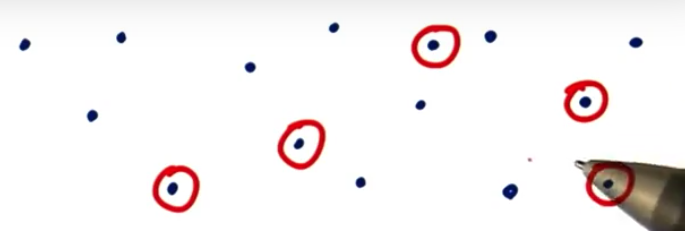
我们将这一自由度概念应用到样本和总体中,假设上图这些是总体中的值,我们可以从该总体中选择任意 n 个值,形成样本量为 n 的样本,如果 n 是 5,假设我们选择了这红圈中的5 个值,自由度是 5,如果我们选择 n 个样本值,自由度则是 n。我们还需要计算样本标准偏差,为此,我们需要知道样本均值,要算出样本均值,我们需要将样本中的每个值相加再除以样本中的值数量,得出 x 拔,意味着样本中的所有值的和必须等于 x 拔乘以 n,这和之前有 n 个值,这些值的和必须等 10 的示例一样,在这个示例中,自由度是 n-1。这一规则同样适用于此处。在我们的总体中,当我们需要选择 n 个样本值时,我们需要满足一定的条件,即第 n 个值必须确保这些值的和等于 x 拔乘以 n,也就是说 n-1 个值可以随意变化,只要第 n 个值使得和为相同的值,从而达到相同的均值即可,称为有效取样数,因为样本标准偏差取决于 x 拔,自由度为 n-1,你可能会问,如果总体标准偏差也使用 x 拔,为何要除以 n 呢?
于总体来说,我们无法像样本那样,用某些值代替其他值,因为总体的所有可能值已经定好了,自由度是指在不影响给定限制条件的情况下,可以自由变换的信息的数量,可以将自由度视作估算其他信息时可有的独立信息数量,在我们知道均值后 只有 n-1 个值是独立的,随着自由度的增大 t 分布将更接近正态分布。
T表格
现在已经不是正态分布,而是 t 分布,我们需要使用新的表格,这个叫做 t 表,和 z 表不同。t 表显示的是临界值,在这里的顶部列行表示的是右尾的面积,左侧表示的是自由度。
http://pan.baidu.com/s/1bBZeZ8
t 分布是由自由度定义的,在 t 分布的 x 轴上是 t 值而不是 z 值,在这种情形下,我们只关心 t 临界值,假设我们有个 t 分布,我们想知道这里的尾部是 10% 即 0.1 时,对应的 t 临界值,假设我们的样本量是 10,所以自由度是 9,这是一个自由度为 9 的 t 分布,我们想知道这个 t 临界值 在这里的尾部,我们要查找 0.1 自由度是 9,我们看到 t 值是 1.383,这个 t 表和 z 表的使用方式基本上一模一样,只是我们要查找的是 t 值,然后判断该 t 值是大于还是小于 t 临界值,而不是查找 z 值并判断该 z 值是大于还是小于 z 临界值。
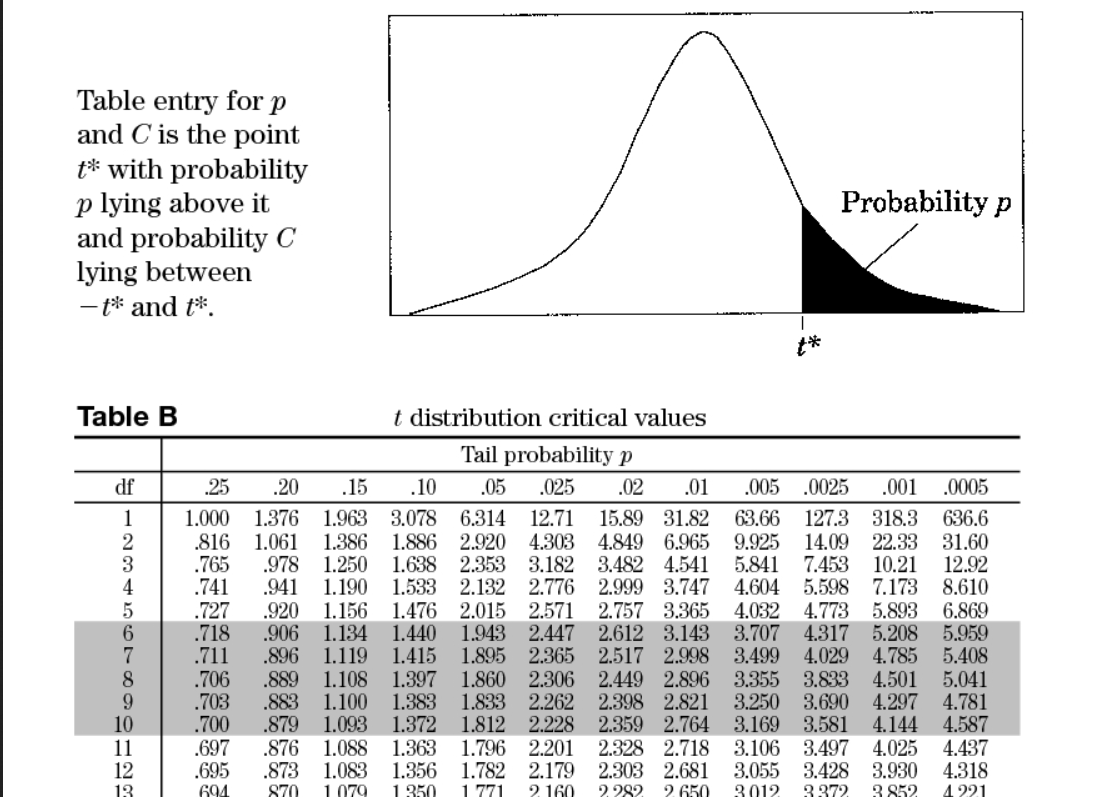
单尾 α 水平是 0.05 时的 t 临界值,即一个尾部的比例是 0.05,自由度是 12

1.782
样本量是 30,α 水平是 0.05 的双尾检验的 t 临界值是多少?对于双尾检验,存在两个临界区,每个尾部一个临界区,因为 t 分布是对称的,所以 t 临界值应该是正负多少?

正负2.045 自由度是 n-1,所以我们的自由度是 29,双尾检验的 α 水平如果等于 0.05,那么每个尾部是 0.025,我们查找尾部概率是 0.025 的位置,在自由度 29 这里,找到 t 临界值是 2.045
样本量是 24,t 值是 2.45,t 值右侧的面积是在多少和多少之间?

0.01-0.02 t 值是 2.45,同时还知道样本量是 24,所以自由度是 23,这里是自由度 23,我们查找 t 值 2.45 在 2.177 和 2.5 之间,该 t 临界值的右侧面积是 2.177 对应的是 0.02 即 2%,2.5 右侧的面积是 0.01,即 1%,表明 2.45 右侧的面积在 0.02 和 0.01 之间。
影响T统计量
和 z 检验一样,当 t 统计量在任一方向远离 0 时,也就是说如果样本均值远离这个总体均值,我们就拒绝零假设,首先我们需要对比样本均值与总体均值,在这种情形下,t 等于样本均值减去总体均值 μ0,再除以标准误差,我们使用的是样本标准偏差,而不是 σ 除以平方根 n。
x 拔越大越能证明样本所来自的总体均值大于我们要对比的这个总体均值。
x 拔越小越能证明x 拔所来自的总体均值小于我们要对比的这个特定值。
x 拔在任一方向离 μ0 越远越能证明 μ 不等于 μ0。
单样本T检验
上面的的统计量针对的是单样本 t 检验,因为我们只有一个样本,均值为 x 拔,我们想知道这个样本来自的总体是否与具有这个均值的总体显著不同,因此,零假设是指总体均值等于某个特定的值 μ0,对立假设可以是 μ 小于 μ0 大于 μ0或者不等于 μ0。当我们计算 t 统计量时,分子是样本均值与这个值的差,而样本均值是总体均值 μ 的点估计值,分母衡量的是总体均值与 μ0 之间,按概率预测的区别,我们知道 α 水平(位于 t 表列标题中),t 表显示了划分 α 水平的 t 临界值,如果 t 统计量大于这些 t 临界值或者负的 t 统计量小于划分 α 水平的负 t 临界值,则拒绝零假设。
下个示例讨论的是地雀的鸟嘴宽度,具体来说,科学家通过观察地雀,做出演化论的假设,通过记录某个特征随时间的变化,例如鸟嘴宽度,我们可以判断周围环境是否在选择特定宽度的鸟嘴,或许有一种特定宽度的鸟嘴可以帮
助这只地雀生存下来,但是有时候因为总体的变化,鸟嘴宽度可能存在随机的波动,某些地雀的鸟嘴要比其他地雀的宽,因此要判断随着时间的推移,总体中的鸟嘴宽度是否存在显著变化,我们需要运用统计学,如果鸟嘴宽度均
值的确显著变宽或边窄了(这称为定向选择),则表明周围环境允许鸟嘴更宽的地雀存活并繁殖下去,假设我们知道所有地雀的平均鸟嘴宽度是 6.07 毫米,这包括过去几年内被研究的地雀,现在假设我们研究的是现今的地雀
样本,我们想知道,现今的地雀的鸟嘴宽度是否不太一样,意味着零假设是现今地雀的总体均值与以前的相等,对立假设应该是什么呢? A.μ 小于 6.07 B.μ 大于 6.07 C.μ 不等于6.07

答案是C
接下来我们需要知道的是样本量和自由度,请点击下面的链接,查看样本数据并计算这两个值,http://pan.baidu.com/s/1eRLuv6q

样本量是 500,自由度则是 499
样本均值和标准偏差是多少?注意,计算标准偏差时,我们是用平方和除以 n-1,然后再取平方根

平均值约为 6.47,样本标准偏差约为 0.4
现在来计算 t 统计量,t 统计量等于 x 拔,即样本均值,减去总体均值 μ然后再除以标准误差即 s/√n ̄

t=(6.47-6.07)/(0.4/√500 ̄)结果约为 22.56
现在已经知道 t 统计量,我们是接受对立假设还是零假设?

我们将拒绝零假设,因为 t 统计量非常大,我们知道无论选择哪种显著水平(最小的通常是 0.01),我们的 t 值都会超出 t 临界值范围,我们拒绝零假设是因为达到这个 t 统计量的概率,即从均值为 6.07 总体中获得这个样本均值的概率非常非常的小,这是 P 值,是指零假设为真时达到该值的概率,因为概率太小,所以可能存在某些情况,零假设可能不为真,这种鸟嘴宽度的地雀来自完全不同的新总体,均值不等于 6.07。
P值
当我们进行单尾检验时,P 值如果为正,则是指 t 统计量之上的概率,如果 P 值为负,则是 t 统计量之下的概率。但是对于双尾检验来说,P 值则是大于该 t 统计量的概率和小于负的 t 统计量的概率,如果一开始得出负的 t 统计量,也是相同的情况,P 值等于小于该 t 统计量的概率加上大于正的 t 统计量的概率,当 P 值小于 α 水平时我们会拒绝零假设。
假设存在以下样本,这个样本均值在 α 水平是 0.5 时与 10 显著不同吗?首先请算出 t 统计量,注意 S 要使用样本标准偏差。
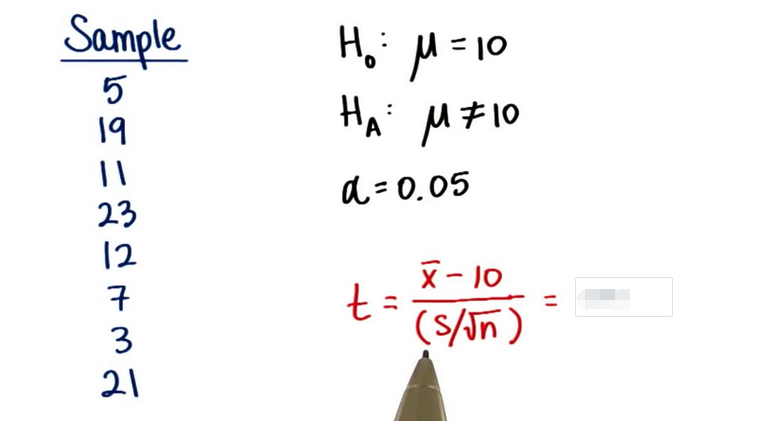

对于 x 拔 即样本均值,我们将这些数字全相加然后除以 8,结果为 12.625,对于样本标准偏差,我们取每个值减去均值 x 拔的平方根然后求平方,再相加并除以 n-1,结果约为 7.596,再将这些值代入 t 统计量的计算公式中,结果约为 0.977


