（四）差异性

学习如何使用方差和标准偏差定量分析数据的分布。并学习如何使用箱线图和四分位距找出差异值。

值域

比如说你们正在辩论是否要获取社交网络账号，可以看一下1000名抽样中有社交网络帐号的人的工资分布图，以及从一般总体中抽样的1000个人的工资分布图，一般总体也可能包括有社交网络帐号的人，如果这是分布图1，
这是分布图2，那么均值1___均值2，中位数1____中位数2，众数1____众数2，大于、等于还是小于？

平均值、中位数和众数似乎是一样的

众数
图1，众数是y轴值为330的那一列，对应的x轴的值为40000-50000；图2，众数是y轴值为187的那一列，对应的x轴的值为40000-50000

中位数
样本为1000，图1中，33+155=188+330=518，中位数在y轴值为330的那一列中；图2中，22+43+92+156=313+187=500,对应的x轴的值都为40000-50000

均值
2图的均值大约都为50000

如果对这两个分布图而言 平均值、中位数和众数都相同，那么两个分布图间有什么区别？答案可能不止一个

    A.□ 有社交网络帐号的人的工资更一致
    B.□ 一般大众的工资更为一致
    C.□ 工资非常高的人没有社交网络帐号
    D.□ 工资非常低的人有社交网络帐号
    E.□ 一般大众的工资分布图更分散

AE

我们可以看到图2比图1更分散，我们如何对分散程度进行量化呢？我们如何看待最大值和最小值以及如何找出它们间的距离呢？比如说这里，图1的最大值是78600，最小值是21180，而图2最大值是116020，最小值是7350，那么图1和图2值域（最大值减去最小值）是多少呢？

图1值域是78600减去21180，结果是57420
图2值域是116020减去7350，结果为108670

从结果之中，我们可以图2的值域比图1的值域大一些，这是一个衡量分布图有多分散的方法，值域很容易计算和理解，值域还提供了一个关于数据如何分散的概要信息，然而，正如我们以前看到的那样，方便是有代价的，当我们将新的数据加入数据集时，值域有时会改变，我们可以在中间加入大量的数据值，而这样就会改变数据分布的形状，但不会改变值域，如果我们在高于最大值的地方加入一个值就会改变我们数据集的值域，值域不包括细节信息，因为值域是仅仅在两个数据的基础上得出的，这些数据在整个分布中是最极端的值，这些极端值不大可能代表分布图的其余值。

 四分位距IQR

统计学家处理异常值的一种方法就是忽略分布中的上尾和下尾。我们只需考虑中间的数据值。忽略尾部是什么意思？习惯上，统计学家会忽略较低的 25% 和较高的 25%。假设您要处理 8 个数据值。我们将忽略两个最小值（或最低的 25%）和两个最大值（或最高的 25%）。也就是说我们只需关心中间的这些值即可。

 

 注意：

虽然建议去除上下各 25% 的数据点，但我们在去除数据点时还需要特别谨慎，特别是在数据量不大的情况下，去除一半的数据点会让我们丢失大量数据的信息。

一般来说，在去除数据点前，我们建议首先将数据点通过图像表述出来（直方图、散点图、箱线图等），这样可以帮助你获得对数据整理分析的了解。然后，基于项目的背景，判断你更关心数据的哪一部分（大多数正常数据，还是小部分异常数据），因为在一些项目背景下，你可能更关心那些异常值，比如在 数据分析（进阶）课程的安然数据分析中，那些工资异常高的人更有可能腐败。最后，是基于现有的数据量作出决定，究竟是直接丢弃部分数据还是对部分作出调整，亦或是有保留地接受所有数据。特别记住一点，没有一种分析方法100%正确，但我们总可以尝试根据不同的需求找到一种最合理的方法。

Q1

根据下面的分布图，你认为第一个四分位数将在25000（下图第一个绿色箭头）处吗？或者在左边或右边？（提示：第一个四分位是 25% 的数据低于该点、75% 的数据高于该点的位置。）

 

如果我们看一下这个图表，会发现看上去是50000将数据分拆成了两半，左侧有500个值，右侧有500个值，左侧500分拆一半是250，我们知道有250个值时出现第一个四分位数，四分位数就在下图X轴第二个绿色箭头的地方，就在25000的右边

 下列表格是从上图中抽出的10个样本，我们要找出第一个四分位数，此后会称其为一般总体的 Q1，我们还要找出第三个四分位数 称其为 Q3，

首先我们将数据分成两半，得到上面的五个值和下面的五个值，之后，我们寻找这一半数据的中位数它是38801，这是 Q1，也就是第一个四分位数的值，接着找出另一半数据的中位数，它是56863 这是 Q3，我们称中位数为 Q2，那么我们得到的新四分位差将是 Q1 和 Q3 之间的距离，去掉上、下末端值 或者说去掉上、下25%后，18062就是我们得到的新四分位差

 在得出Q3减去Q1结果时，实际是在计算四分位差，缩写是 IQR。

下列关于IQR的说法是错误还是正确？
    1.几乎 50% 的数据在 IQR 间。
    2.IQR 受到数据集中每一个值的影响。
    3.IQR 不受异常值的影响。

1.正确
2.错误
3.正确

异常值

异常值是究竟什么？比如在下列这些数据中，你认为异常值会在哪里？是60000、80000、100000还是200000？看下这些数据，你认为哪些数据与整体数据集相去甚远呢？

或许这些值都不是异常值，因为可以看到10000000其实是极限数据值，如果它是数据集的组成部分，那么这些值或许不是异常值，这就是为什么我们在统计学上有专门的方法来计算一个值是否是异常值

如果一个值小于第一个四分位数减去1.5倍的IQR或者大于 Q3 加上1.5乘以 IQR，则这个数就被认为是异常值。

这里你可以看到四分位差（IQR）是4944，你知道 Q1 是49191，Q3 是54135，这是根据已被普遍接受的异常值定义得出的，请以统计学方式确定哪些值被认为是异常值。

我们来计算不被视为异常值的那些值的值域，Q1 是49191，四分位差是4944，也就是说 Q1 减去1.5再乘以 IQR，49191-1.5*4944=41775，小于这个数的任何数都被视为异常值，我们还知道，Q3 是54135，54135+1.5*4944=61551，任何大于这个数的值也都是异常值，这表示，从统计学角度看，80000,100000,200000是异常值，但60000美元不是。

箱线图

箱线图（Boxplot）也称箱须图（Box-whiskerPlot），它是用一组数据中的最小值、第一四分位数、中位数、第三四分位数和最大值来反映数据分布的中心位置和散布范围，可以粗略地看出数据是否具有对称性。通过将多组数据的箱线图画在同一坐标上，则可以清晰地显示各组数据的分布差异，为发现问题、改进流程提供线索。

 具体可以参考http://blog.csdn.net/zhanghongju/article/details/18446131

均值

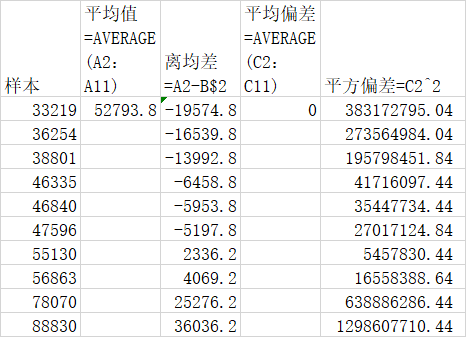
下面是我们一般总体中的抽样，平均值是 $52793.80，如果你还记得计算过程是将每个数相加，因为有10个值，将相加的总和除以10得到平均值。

离均差

离均差的计算方法是用每个值减去平均值。

平均偏差

平均偏差是离均差的平均值。

但是，现在我们遇到了问题，我们的平均偏差为0，这显然无法很好地测量分布，这会让我认为，如果我们再三得到相同的数据点，则其分布将为0。但是现在整条数轴上有许多数据点，这将导致某种程度的分布，因此，如果我们仍然得到值为0的平均偏差，则不能通过这种方式来测量分布，问题在于负值将抵消正值。

测量分布时，我们不关心数值是高于还是低于均值，我们关心的仅仅是它们与均值相差多少？因此，我们该如何确保正值偏差和负值偏差不会相互抵消呢？

平方偏差

消除这一些负值的另一个方法是取每个离均值的平方值，换句话说，我们将每个值乘以它本身。

平均平方偏差

平均平方偏差即是平方偏差的平均值。

平均平方偏差是291622740 它有个非常特殊的名称，叫做方差。

标准差

 标准差也被称为标准偏差，标准差=方差的算术平方根，在概率统计中最常使用作为统计分布程度（statistical dispersion）上的测量。

标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。它反映组内个体间的离散程度。

 公式为

 贝塞尔校正

通常，抽样中会低估了总体中差异性的数量，因为抽样往往是总体居于中间的值，特别是在正态分布中 多数值居于中间位置，因此我们从正态分布的总体中抽样时，多数值也在此处附近，因为多数值在这个区域内，因此抽样中的差异性将少于整个总体的差异性，为了纠正这一现象，我们使用贝塞尔校正系数，我们把除以 n用除以 n 减 1 代替，在方差的处理中也是一样的