并查集学习
模板
class DisjointSet {
public:
int count = 0;
vector<int> parent;
DisjointSet(int n) {
this->count = n;
parent = vector<int>(n);
for (int i = 0; i < n; i++) parent[i] = i;
}
int find(int p) {
while (p != parent[p]) {
parent[p] = find(parent[p]);
// parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
void unions(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootP] = rootQ;
--count;
}
};
- 解决分群、分类别的问题
题目列表
- LC.547.朋友圈
- LC.200.岛屿数量
- LC.130.被围绕的区域
- LC.685.冗余连接II(困难)
- LC.684.冗余连接
LC.200.岛屿数量
- 除了搜索递归回溯的方法,此题也适用于并查集
- 简单思路:对所有陆地为1的块进行如上面模板一样的parent[i]=i操作,此处是parent[im+j]=im+j,其中i是行号,j是列号,m是行长度;为0的则输入-1占位,然后再一次遍历,此时只需要判断某位置的下方和右方是否有为1的陆地然后做union操作即可
class DisjointSet {
public:
int count;
DisjointSet() {
count= 0;
}
void insert(int i) {
parent.push_back(i);
if (i != -1) ++count;
}
int find(int p) {
while (p != parent[p]) {
parent[p] = find(parent[p]);
p = parent[p];
}
return p;
}
void unions(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
--count;
}
};
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size();
if (n <= 0) return 0;
int m = grid[0].size();
if (m <= 0) return 0;
DisjointSet handler;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') handler.insert(i*m+j);
else handler.insert(-1);
//cout << handler.count << endl;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') {
grid[i][j] = '0';
if (i + 1 < n && grid[i+1][j] == '1') handler.unions((i+1)*m + j, i*m+j);
if (j + 1 < m && grid[i][j+1] == '1') handler.unions(i*m + j + 1, i*m+j);
}
}
}
return handler.count;
}
};
LC.130.被围绕的区域
-
题意:
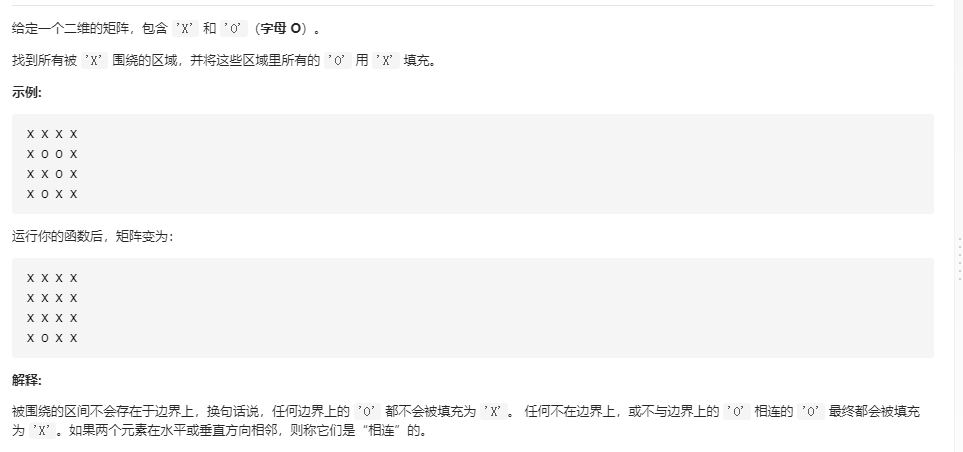
-
思路:并查集方案
- 引用上面的模板,然后增添一个dumy冗余节点,所有边节点都与之unions,然后所有节点都与其四连通的节点相连,然后最后再遍历一次判断与dumy冗余节点相连与否来确定节点是O还是X
class Solution {
public:
void solve(vector<vector<char>>& board) {
int n = board.size();
if (n <= 0) return;
int m = board[0].size();
if (m <= 0) return;
DisjointSet handler(n*m+1);
int dumyNode = n*m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 边界元素与dumyNode连接
if (board[i][j] == 'O' && (i == 0 || i == n-1 || j == 0 || j == m-1)) {
handler.unions(i*m+j, dumyNode);
}
// 然后下右判断连接在一起
if (board[i][j] == 'O') {
if (i+1 < n && board[i+1][j] == 'O') {
handler.unions((i+1)*m+j, i*m+j);
}
if (j+1 < m && board[i][j+1] == 'O') {
handler.unions(i*m+j, i*m+j+1);
}
}
} // end for j
} // end for i
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'O' && handler.find(i*m+j) != handler.find(dumyNode)) {
board[i][j] = 'X';
}
}
}
}
};
LC.685.冗余连接II(困难)
-
题意:
- 有向图
- 有从1——>N的N个节点
- 给出N条有向边
- 有根树一般N个节点只需要N-1条边,但给出N条,因此肯定存在“冲突”或者“循环”或者“循环”+“冲突”
- 任务是找出出现在(给出的有向边的)最后面的删去可以使树合理的边
-
思路:
- 经分析,只有三大情况:
- 1.纯冲突,如1->2,1->3,3->2。此时2有两个父节点,此时删去3->2(删除第二次出现引起冲突的边)
- 2.纯循环,如1->2,2->3,3->1。此时形成循环,删去3->1(删去属于循环的最后出现的边)
- 3.循环+冲突,如1->2,2->3,3->1,4->1,此时形成循环+冲突,删去3->1(删去冲突+循环节点在循环中作为dst的那一条边)
-
实现:
- 对于纯冲突,可以直接开数组(哈希表,因为是从1——>N,所以直接数组就好了)来存储其父节点编号——>初始化为自身编号,当遇到非自身编号时已证明出现冲突,记录该有向边即可
- 对于纯循环,使用并查集解决(首先忽略边的有向性,将能“围成环”的节点组成一个“集合”)
- 因为只有N条边,引起冲突时有两种情况,同时循环或者不循环
- 不循环那直接记录即可
- 循环,经过上面的思路分析,最后删除的也是循环内的冲突边,所以直接记录该条冲突循环边即可
- 因为只有N条边,引起冲突时有两种情况,同时循环或者不循环
- 这样通过互斥就解决了有向边与并查集的矛盾
class Solution {
public:
class UnionSet {
public:
UnionSet(int n) {
parent.resize(n+1);
N = n + 1;
for (int i = 0; i < n+1; ++i) {
parent[i] = i;
}
}
int find(int idx) {
return parent[idx] == idx ? idx: find(parent[idx]);
}
void unions(int i, int j) {
parent[find(i)] = find(j);
}
private:
vector<int> parent;
int N;
};
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int N = edges.size();
vector<int> parent(N+1);
int idx = 0;
for_each(parent.begin(), parent.end(), [&](int& val){val = idx++;});
UnionSet us(N);
int conflictIdx = -1;
int cycleIdx = -1;
for (int i = 0; i < N; ++i) {
if (edges[i][1] != parent[edges[i][1]]) { // 冲突
conflictIdx = i;
} else {
parent[edges[i][1]] = edges[i][0];
if (us.find(edges[i][0]) == us.find(edges[i][1])) { // 循环
cycleIdx = i;
} else {
us.unions(edges[i][0], edges[i][1]);
}
}
}
if (conflictIdx == -1) {
return edges[cycleIdx];
} else {
if (cycleIdx == -1) {
// 先出现的是非循环冲突边,所以当记录冲突的时候将循环边计入循环idx,此时直接返回冲突边即可
return edges[conflictIdx];
} else {
// 先出现的是循环冲突边(此时正常计入parent中形成该边的父子映射),所以当记录冲突的时候将非循环边计入冲突idx,通过冲突idx找到冲突循环节点,然后通过parent数组映射到其在循环内的父节点中即可
return {parent[edges[conflictIdx][1]], edges[conflictIdx][1]};
}
}
vector<int> res(2);
return res;
}
};
LC.684.冗余连接
- 题意:与上一题类似,转换为无向图
- 因为是无向图,所以就没有冲突的说法,即只需要考虑循环,那么删掉最后一条出现的边即可(利用并查集直接告诉完成)
class UnionSet {
public:
UnionSet(int len) {
N = len;
parent = vector<int>(N);
for (int i = 0; i < N; i++) parent[i] = i;
}
int find(int p) {
while (p != parent[p]) {
parent[p] = find(parent[p]);
p = parent[p];
}
return p;
}
void unions(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP != rootQ) parent[rootP] = rootQ;
}
private:
vector<int> parent;
int N;
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int idx;
int len = edges.size();
UnionSet us(len + 1);
for (int i = 0; i < len; ++i) {
if (us.find(edges[i][0]) == us.find(edges[i][1])) {
return edges[i];
} else{
us.unions(edges[i][0], edges[i][1]);
}
}
return vector<int>(2);
}
};
posted on 2020-08-07 01:01 sacredMoonRainTown 阅读(64) 评论(0) 编辑 收藏 举报


