Week6 作业 D - CSP 201812-4 数据中心
题面:
思路:
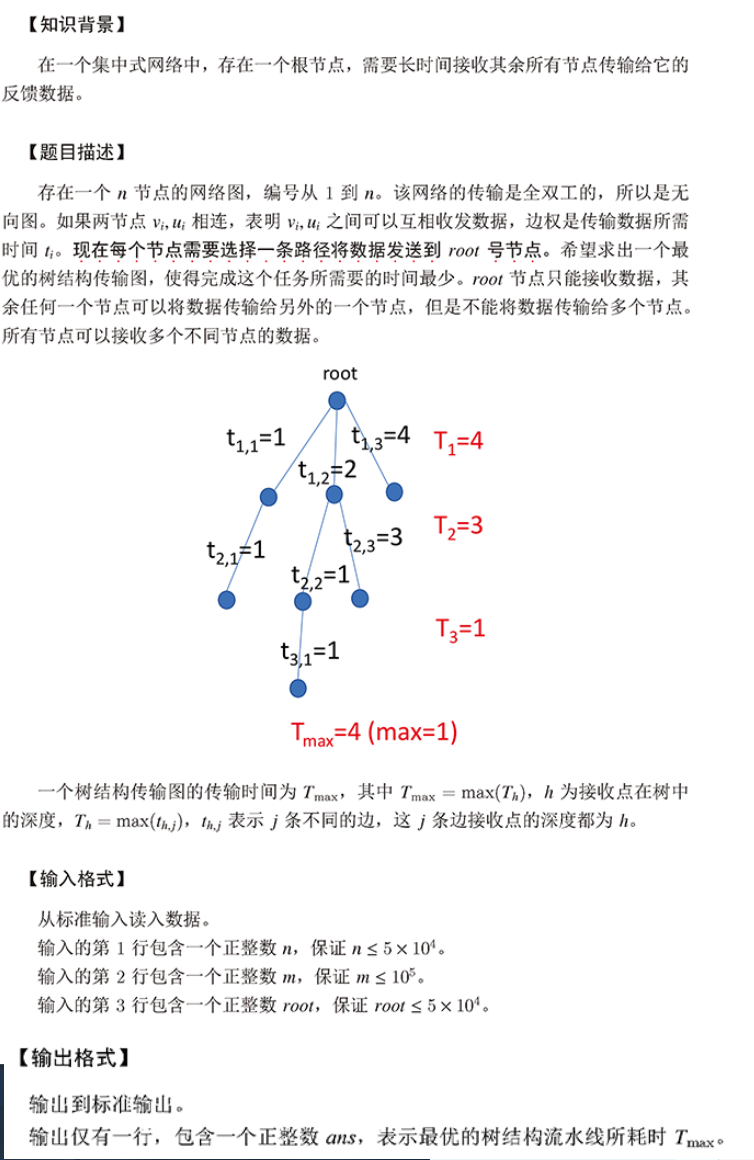
题目很长,但主要信息无非是:无向图,保证每个点都必须有到点ROOT的路径,要求使这些路径中权值最大的边的值最小。
既然每个点都能到ROOT,那么这个图就是一个联通图(每对点之间都有路径,因为总是可以间接经过ROOT)。
我们知道,最小生成树一定是瓶颈生成树,即最小生成树中最大的边,一定是所有生成树的最大边中最小的。
求最小生成树,最后一条加入的边就是最大的边,就是答案。
代码:
1 //求 能使这个图联通时,最大边的权值最小 2 //最小生成树一定是瓶颈生成树 3 #include <cstdio> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 const int MAXN=1e5+5; 8 int n,m,root; 9 int tot; 10 int fa[MAXN]; 11 struct e 12 { 13 int u,v,w; 14 bool operator < (const e &x) const 15 { 16 return w<x.w; 17 } 18 }edge[MAXN]; 19 int find(int x) 20 { 21 if(fa[x]==x) return fa[x]; 22 fa[x]=find( fa[x] ); 23 return fa[x]; 24 } 25 void unite(int x,int y) 26 { 27 int root1=find(x),root2=find(y); 28 fa[root1]=root2; 29 } 30 int main() 31 { 32 cin>>n>>m>>root; 33 for(int i=1;i<=m;i++) 34 { 35 int u,v,w; 36 scanf("%d %d %d",&u,&v,&w); 37 tot++; 38 edge[tot]={u,v,w}; 39 } 40 sort(edge+1,edge+tot+1); 41 42 //kruskal 43 for(int i=1;i<=n;i++) fa[i]=i; 44 45 int num=0; 46 for(int i=1;i<=tot;i++) 47 { 48 int u=edge[i].u, 49 v=edge[i].v, 50 w=edge[i].w; 51 if( find(u)==find(v) ) continue; 52 else unite(u,v),num++; 53 if(num==n-1) 54 { 55 cout<<w<<endl; 56 return 0; 57 } 58 } 59 return 0; 60 }