[css] transform matrix
概述
/* 2D */
transform: matrix(1, 0, 0, 1, 0, 0);
/* 3D */
transform: matrix(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1);
上面两行 css 代码其实什么变换都不会做,因为那是变换的默认状态,即没有变换。但是其中使用到了 matrix,翻译成中文叫做:矩阵。
更多的时候,我们使用类似如下语法:
transform: translateX(100px) rotateZ(30deg);
如上代码所示,一目了然,要做什么变换一看就知道了。但其实,这只是一个语法糖,其底层依然使用的是 matrix。
向量
什么是向量
向量:空间中的箭头
这个箭头由两个因素决定:方向 和 长度,
先把目光局限在二维空间下,如图:
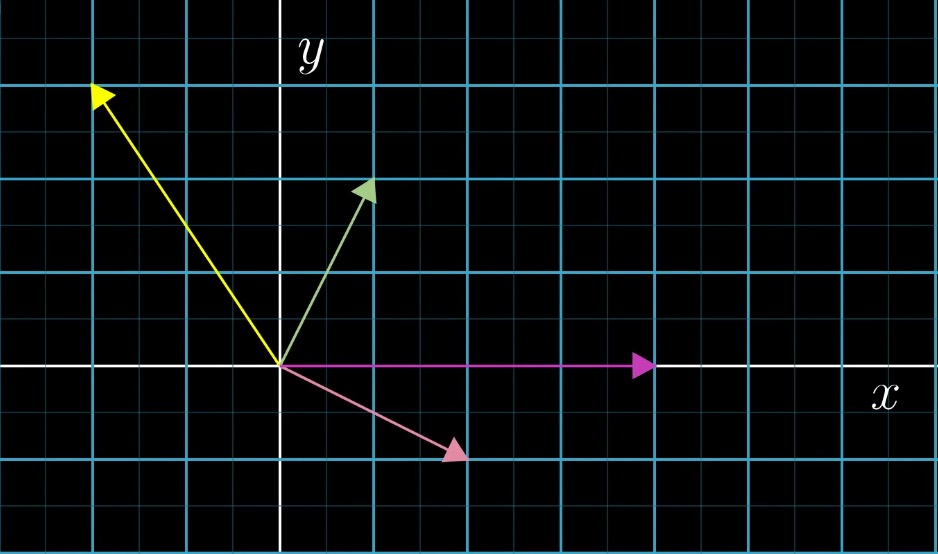
上图中,在一个坐标系中画了四个不同长度和方向的箭头,每个箭头从原点发出,他们代表了二维空间中的四个向量,在线性代数中,向量通常以原点作为起点。
向量:是有序的数字列表
在坐标系中任意选取单位长度,这样就能够使用一个一个的刻度来标刻这个坐标系,选取特定的方向为x/y轴的正方向,那么不难看出,每一个向量,都可以用唯一的一个坐标来表示,同样的,坐标系中的每一个坐标都对应着一个唯一的箭头(向量),如下图:
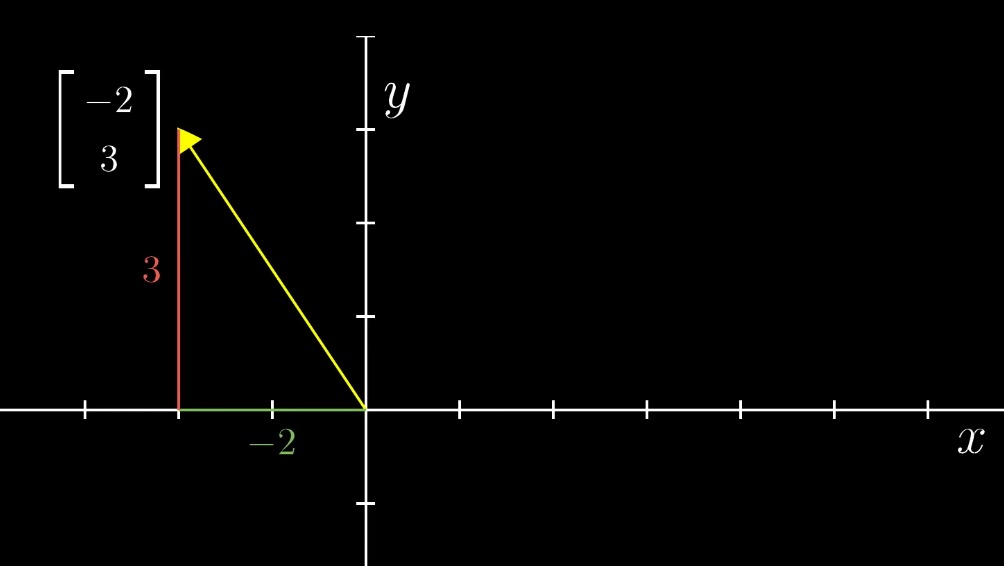
在坐标系中,由于坐标通常用来标示一个点,如 P(2, 8) 表示点 P 的坐标为 (2, 8),为了区分点和向量,在表示向量时,通常把坐标竖着写,然后用一对儿中括号来描述,如上图中的(-2,3)
在三维空间也是一样的道理,如下图,唯一不同的是,每一个向量由 x/y/z三个数字组成的坐标来表示:
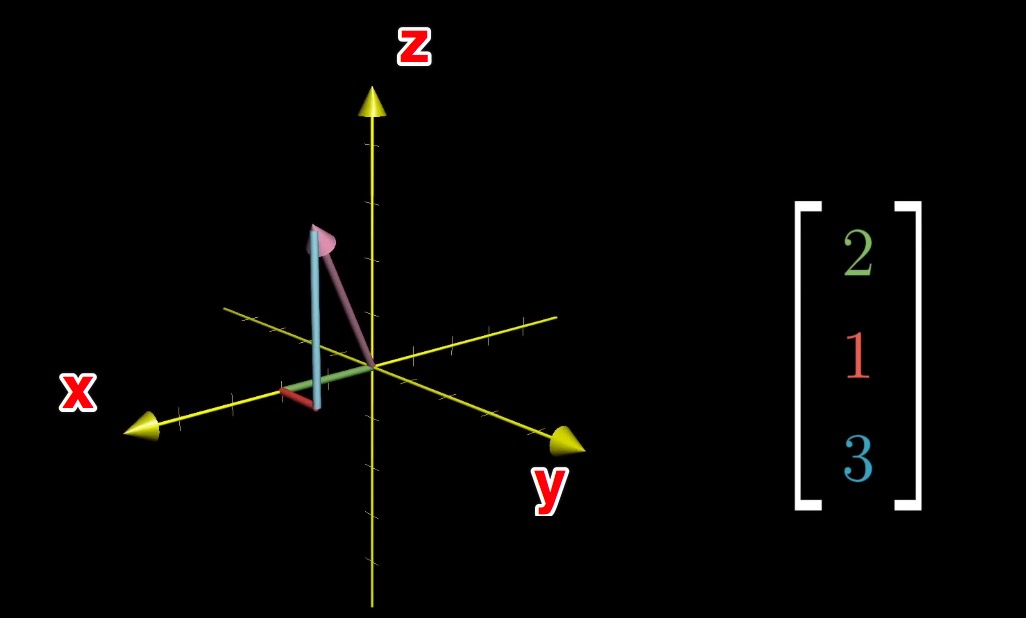
对于向量,只需要知道它是“空间中的箭头”或者“有序的数字列表”这就足够了。
基向量
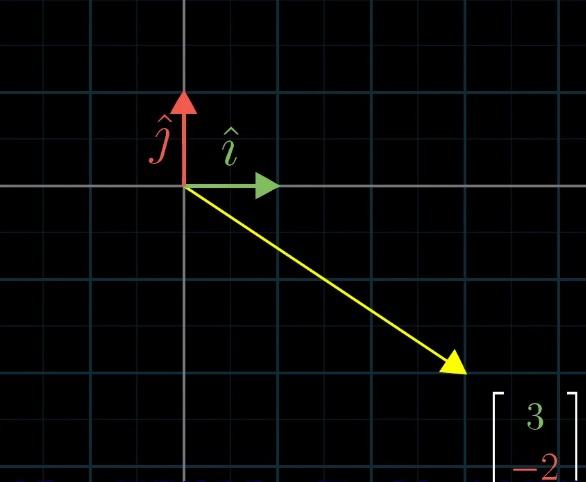
基向量,也叫单位向量,是单位长度为1的向量,如下图中:i帽 和 j帽 就是这个二维坐标系的基向量:
线性变换
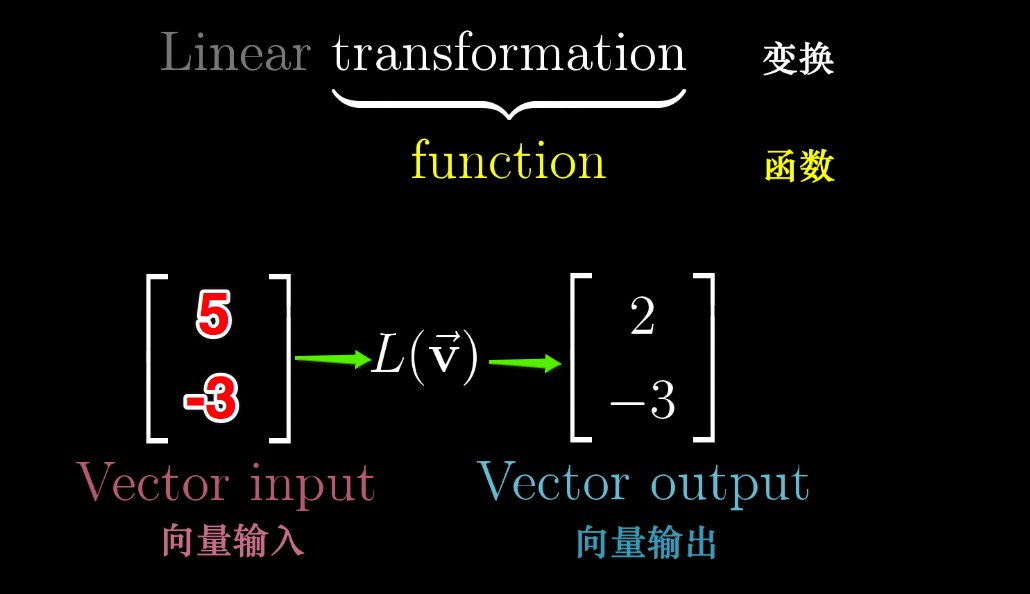
“变换”本质上是“函数”的一种花哨的叫法,与在数学中的概念类似,函数接收输入的内容,并输出对应的结果,如图:

变换也是同样的道理,只不过接收向量作为输入,并输出变换后的向量:
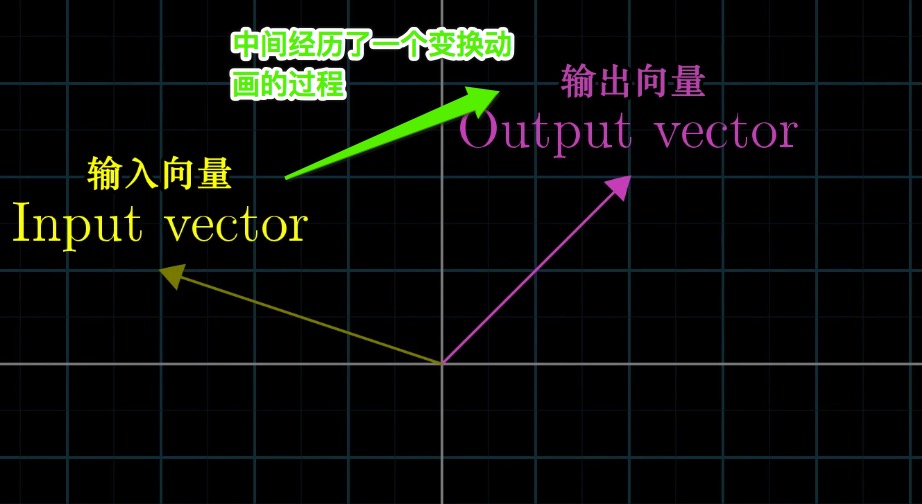
既然 “变换” 与 “函数” 本质相同,那么为什么叫变换而不叫函数?实际上可以把这个输入输出的过程,看做一个向量从初始状态到最终状态的一个变化过程,如下图:
宏观情况下,目前只讨论一个向量的变换.
二维空间的一整个平面,可以看做是由无数个向量组成(或者无数个点组成,因为每一个点唯一标识一个向量,所以这里说平面由无数个向量组成),假如这无数个向量同时做相同的变换,那其实就可以看做是平面的变换:
变换前:

变换后:

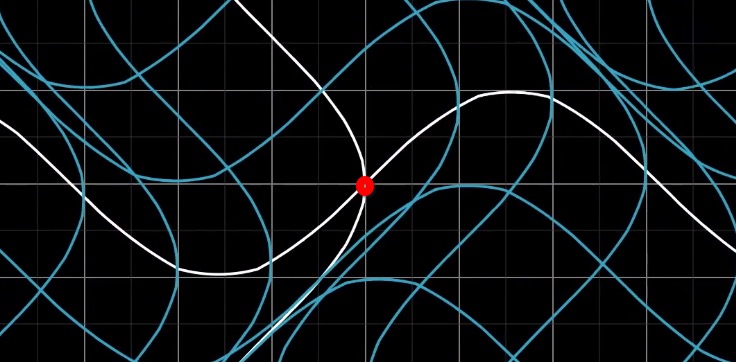
不过,并非所有变换都叫做线性变换,线性变换必须要满足下面两个条件:
- 1、直线在变换后仍然为直线,不能有所弯曲
- 2、原点不能移动
如下变换,就不是一个线性变换,因为直线变成了曲线:
如何用数值描述线性变换?
空间的变换也可以说是向量的变换,而向量在空间中,可以用一组有序的数字列表来表示(即向量的坐标),所以向量变换前后,必然会引起“有序数字列表的变换”,那么否可以用数字去描述变换呢?
空间中的任意一个向量都可以看做是:基向量变换后的和向量,如下图:
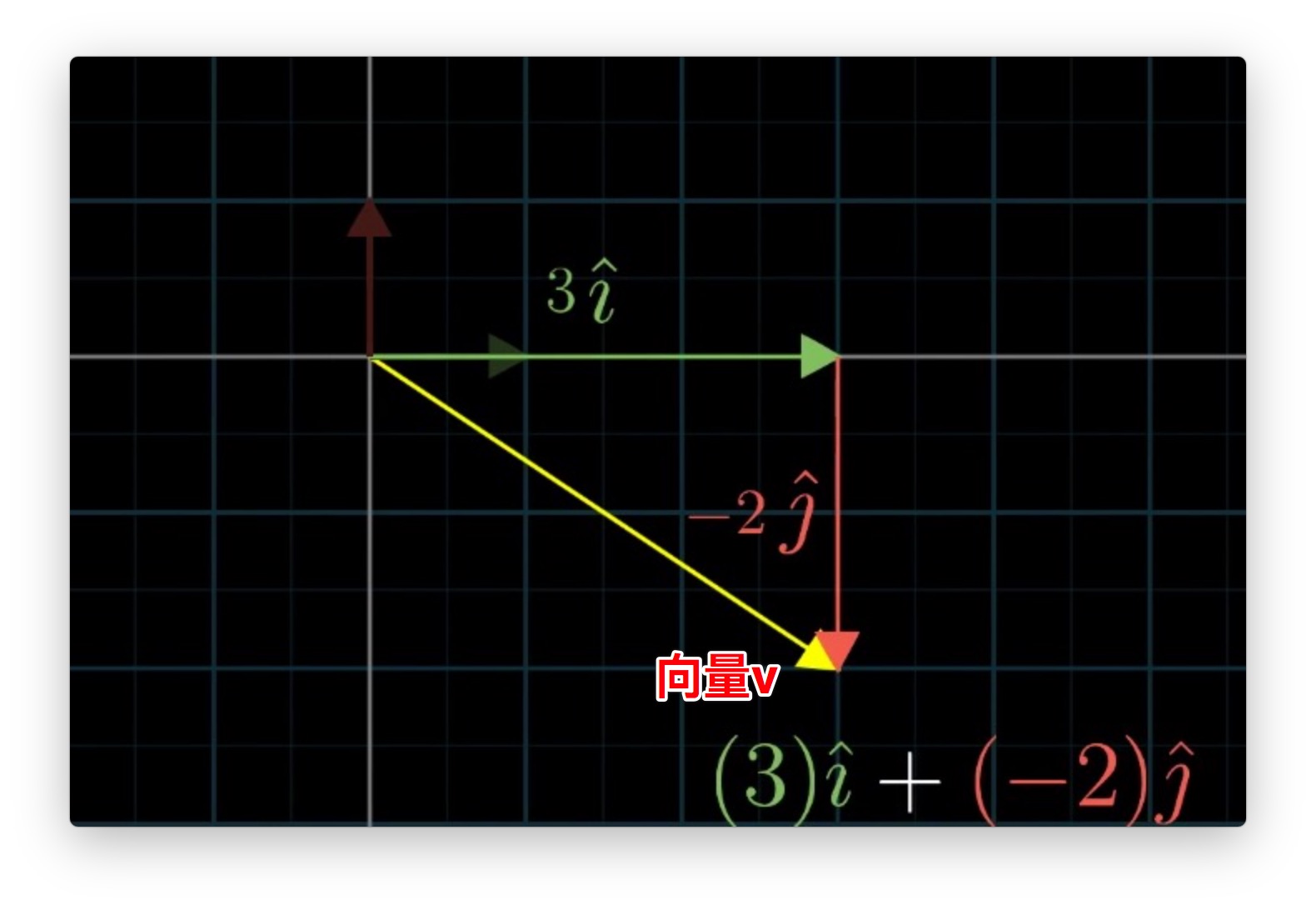
向量 v 的坐标是 (3,-2),如果把 3 和 -2 看做两个标量,也就是纯数字,那么向量 v 可以看做是基向量被标量缩放后相加得到的和向量: v = 3i + (-2j)
假如有向量 v = -1i + 2j,如下图:
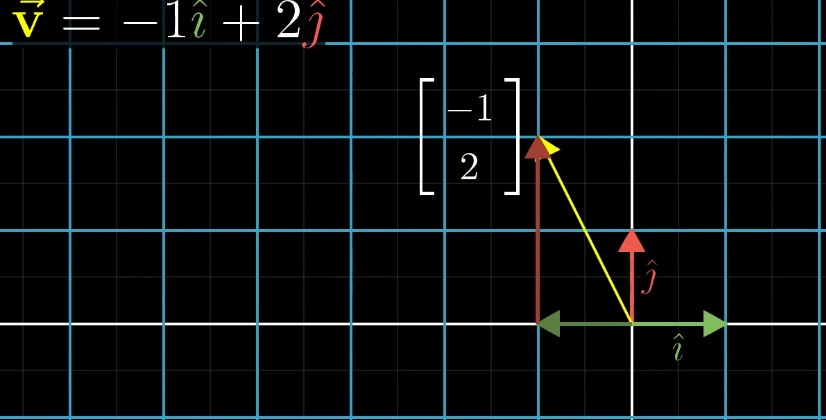
此时,基向量 i 的坐标是 (1, 0)【注意:为了方便,这里就用圆括号代表向量的坐标,下同】,基向量 j 的坐标是 (0, 1),假设经过了某些变换之后,基向量 i 的坐标变为 (1, -2),基向量 j 的坐标变为 (3, 0),如下图:
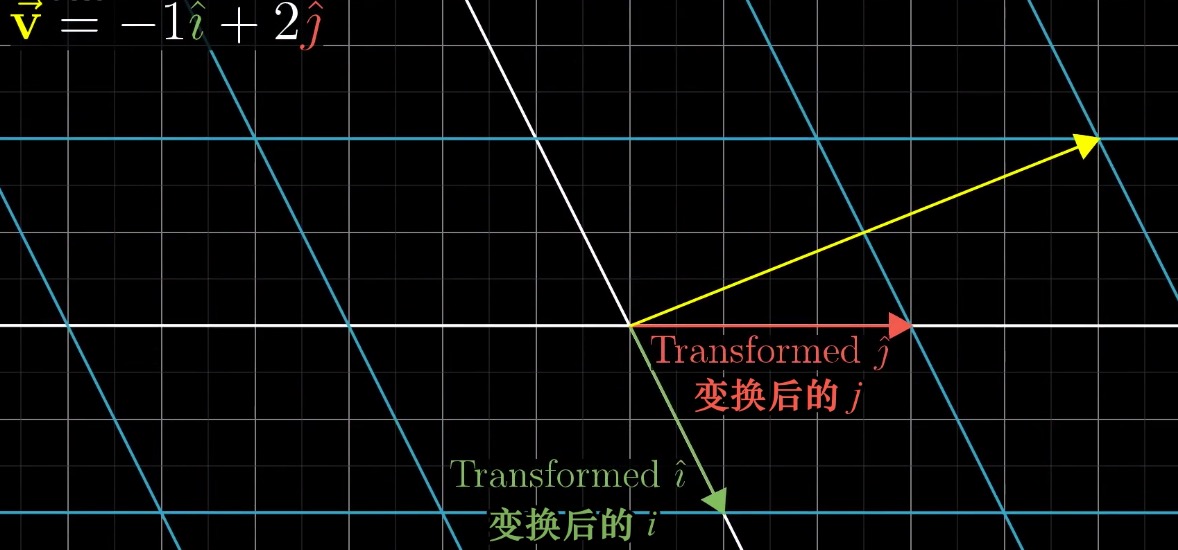
那么变换后的向量 v 依然满足 v = -1i + 2j,如下:

以上例子所描述的事实,实际上是线性变换的性质的推论,该性质可以从几何角度表述为:线性变换后的网格平行且等距。
既然线性变换前后都满足该线性关系:v = -1i + 2j
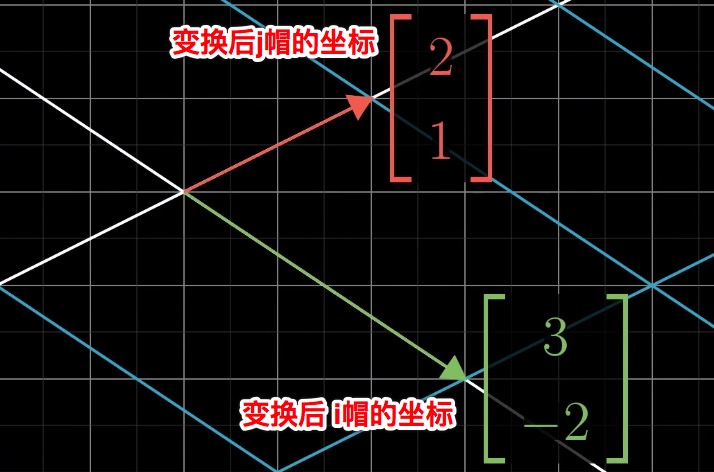
那么很容易根据变换后 i帽 和 j帽 的坐标推算出变换后 v 的坐标:
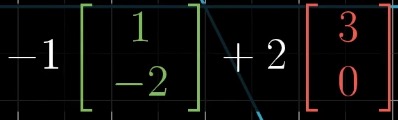
也就是 (5, 2)
那么是否可以认为,给定任意一个向量,其坐标 (x, y),可以通过变换后的基向量的坐标推断出该向量变换后的坐标呢?
答案是肯定的,假如基向量变换后的坐标 i帽 和 j帽 如下图:

那么任意向量 (x, y) 在经过变换后的坐标计算如下:
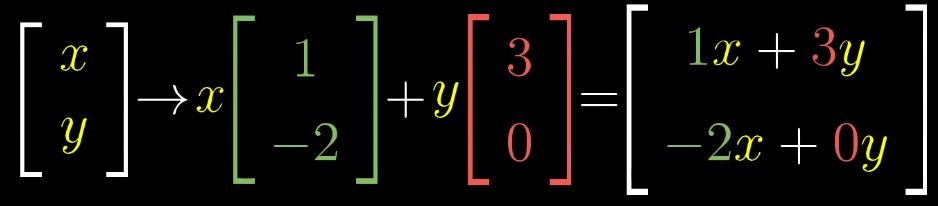
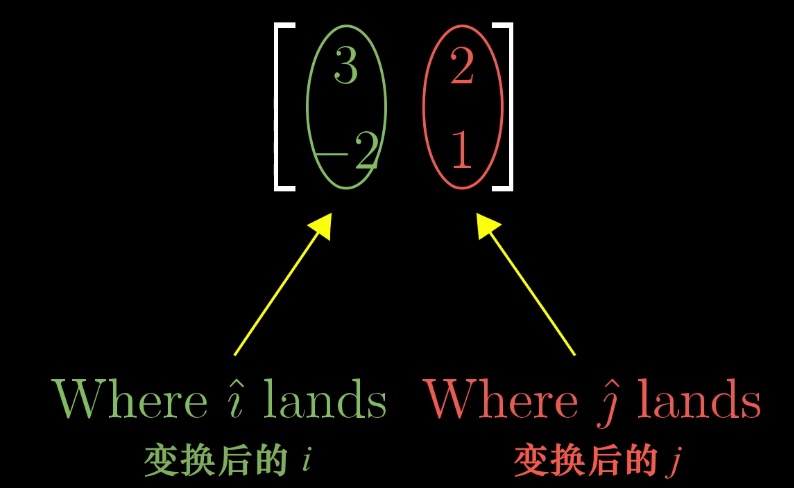
所以 二维空间的线性变换仅由四个数字完全确定,这四个数字就是基向量 i 变换后 i帽 的坐标,以及基向量 j 变换后 j帽 的坐标,如下图:
只需要四个数字,就确定了二维空间的一个变换。通常把这四个数字放到一个 2 x 2 的格子中,称之为 2 x 2 矩阵:
现在,当再看到 2 x 2 矩阵的时候,第一几何直观反映应该是:它描述了一个二维空间的变换。
把情况一般化,如下图:
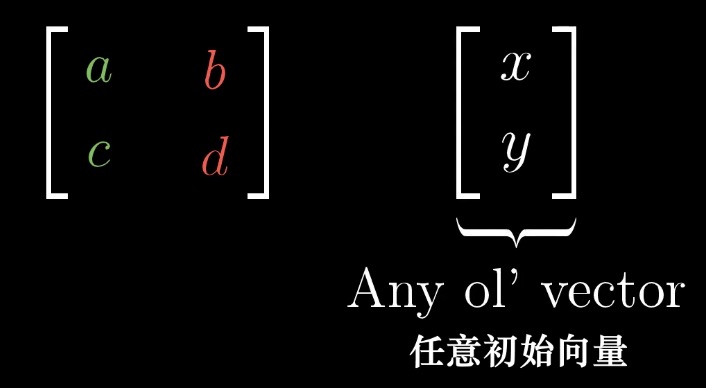
有一个 2 x 2 的矩阵 [a, c] [b, d],其中 [a, c] 是基向量 i 变换后的坐标,[b, d] 是基向量 j 变换后的坐标,那么根据这个变换,以及线性变换的性质,可以推断出任意向量 [x, y] 变换后的坐标:
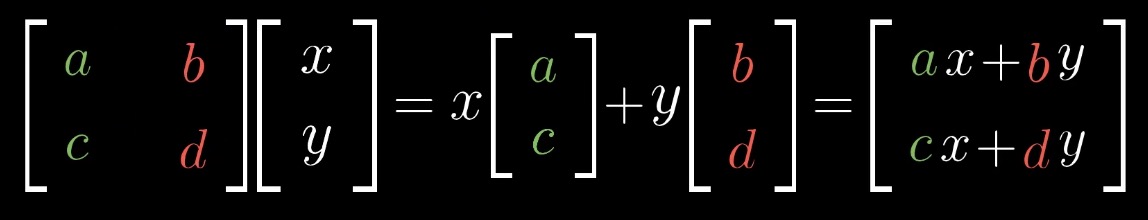
实际上,这就是数学家之所以这样定义 矩阵的向量乘法 的原因。
整理一下思路,首先,对于一个 2 x 2 的矩阵,第一列的两个数是对基向量 i 的变换,第二列的两个数是对基向量 j 的变换,这四个数字组成的 2 x 2 的矩阵,描述了一个对空间的线性变换,可以根据这个变换推断出任意一点(或者任意向量)变换后的坐标。
其实还可以换一个角度考虑,单纯的把 2 x 2 矩阵叫做变换,那么向量与矩阵的乘积,就可以看做是该向量应用了这个变换。其实,这就是矩阵向量乘法的几何意义。
回到 CSS 的 transform
看一下2D变换下 transform 属性的 matrix 写法:
transform: matrix(a, b, c, d, e, f);
//各个参数默认值
transform: matrix(1, 0, 0, 1, 0, 0);
transform 2D变换是一个 3 * 3 的矩阵. 因为位移(translate),线性变换要满足其中一个特点:原点不能移动,但是位移却使原点发生了移动,所以 2 x 2 矩阵满足不了需求,只能再加一列,也就是 3 x 3 的矩阵。
把 matrix 中的 a b c d e f 放到一个 3 x 3 的矩阵中应该是这样的:

其实,在没有位移(translate)的情况下,[a, b] [c, d] 四个数字组成的 2 x 2 矩阵是完全可以描述2D变换的,现在只看由 [a, b] [c, d] 组成的 2 x 2 矩阵:

把 a b c d 四个数字使用默认值替换一下,即:a = 1,b = 0,c = 0,d = 1,如下:

通过之前的介绍,在看到这个矩阵的时候,应该知道,第一列的坐标 (1, 0) 应该是基向量 i 变换后的坐标,但是基向量 i 在变换前的坐标就是 (1, 0),也就是说没有任何变换,同理,基向量 j 也没有任何变换,所以说,这就是 a b c d 默认值设定为下面代码所示的值的原因:
transform: matrix(a, b, c, d, e, f);
// a b c d 默认值为 1 0 0 1
transform: matrix(1, 0, 0, 1, e, f);
//e f 代表原点,默认是0 0
如果把 a 的值从 1 变为 2 那么矩阵如下:

也就是说,基向量 i 的坐标从 (1, 0) 变成了 (2, 0),是不是基向量 i 被放大为了原来的二倍?
举一个通俗的例子:原本单位长度1代表20px,被放大后单位长度1则代表40px。同样的,当把 a 的值从 1 变为 0.5 则意味着把基向量 i 缩小为原来的一半。事实上:在 transform: matrix() 中,修改 a 的值,就是在改变 x 轴方向的缩放比例:
transform: matrix(2, 0, 0, 1, 0, 0);
/* 等价于 */
transform: scaleX(2);
同理,修改 d 的值,就是改变 y 轴的缩放比例:
transform: matrix(1, 0, 0, 4, 0, 0);
/* 等价于 */
transform: scaleY(4);
那么旋转要如何修改 matrix 中的值呢?
其实,想要知道如何修改 a b c d 的值,只需要知道,旋转后基向量 i 和 j 的坐标就可以了,将旋转后的坐标对号填入就可以得到变换矩阵。
在 web 开发中的坐标系和数学中的坐标系在正方向的选取上不太一致,在大家所熟悉的坐标系中,正方向的选取如下:
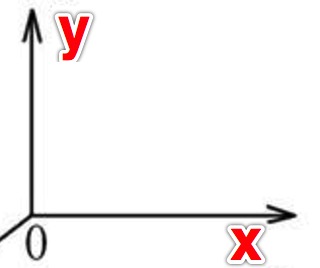
而在 web 开发中,坐标系的正方向选取是这样的:
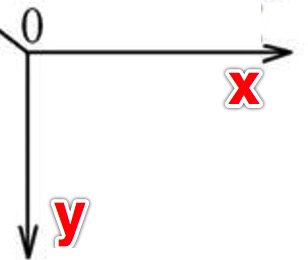
假设将其顺时针旋转 45 度,如下图:
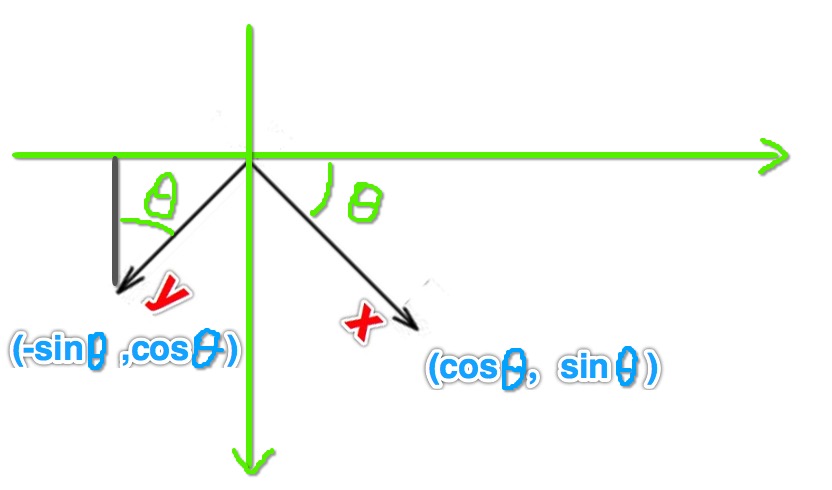
假设,上图中旋转的是单位向量,那么旋转后单位向量 i 的坐标应该是 (cosθ, sinθ),单位向量 j 的坐标应该是 (-sinθ, cosθ),所以如果用矩阵表示的话,应该是这样的:

如果写到 matrix 里,自然就是下面这个样子:
transform: matrix(cosθ, sinθ, -sinθ, cosθ, 0, 0)
所以,如果要顺时针旋转 45 度,下面两种写法是等价的:
/*
* Math.cos(Math.PI / 180 * 45) = 0.707106
* Math.sin(Math.PI / 180 * 45) = 0.707106
*/
transform: matrix(0.707106, 0.707106, -0.707106, 0.707106, 0, 0)
/* 等价于 */
transform: rotate(45deg);
通过上面缩放和旋转的例子知道2 x 2 的矩阵确实能够描述二维空间的变换,这也就是矩阵能够操作空间的原因。在 transform 中,除了缩放(scale)、旋转(rotate) 还有倾斜(skew),对于倾斜,类似于寻找旋转后基向量的坐标一样,只需要根据倾斜所定义的变换规则,找到基向量变换后的坐标就可以了,实际上倾斜对应如下规则:
transform: matrix(1, tan(θy), tan(θx), 1, 0, 0);
无论 缩放(scale)、旋转(rotate) 还是倾斜(skew),都不会是原点发生改变,所以使用 a b c d 四个数字组成的矩阵完全可以描述,但是还有一个 位移(translate),这时,就不得不提到 e f 了,e f 分别代表了 x y 方向的位移:
transform: matrix(1, 0, 0, 1, 100, 200)
/* 等价于 */
transform: translateX(100px) translateY(200px);
至此,transform 使用 3 x 3 矩阵来描述二维空间变换的方式。

除了2D变换,还有3D变换,在 transform 中,使用 4 x 4 的矩阵描述3D变换,但实际上,三维空间的线性变换只需要一个 3 x 3 的矩阵就可以描述了,那么为什么搞了一个 4 x 4矩阵呢?实际上这和在将二维空间的变换使用 3 x 3 矩阵的道理是一样的,那就是位移。
看一下3D变换的 matrix 默认值:
transform: matrix(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p);
transform: matrix(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1);
这十六个数字就是 4 x 4 矩阵的 16 个数值:

如果换成对应数字,是这样的:

类似于 2D 变换一样,其中由
组成的 3 x 3 矩阵用来描述空间的 3D 线性变换,如:rotateX rotateY scaleZ 等等,注意:rotateZ 是 2D 变换。
而 m n o 则分别用来描述位移:translateX translateY translateZ。


