BZOJ 1833 数字计数 数位DP

题目链接

做的第一道数位DP题，听说是最基础的模板题，但还是花了好长时间才写出来。。。。。

想深入了解下数位DP的请点这里

先设dp数组dp[i][j][k]表示数位是i，以j开头的数k出现的次数

有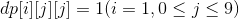 

    

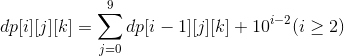
数位dp的题一般都会用到前缀数组，题目要求我们求b-a这个区间里各个数码出现的次数，我们可以分别求出（0，b）和（0,a-1）然后相减即可

具体分析请看代码，写的还算详细

#include <bits/stdc++.h>
using  namespace  std;
typedef long long ll;
ll dp[15][10][10];
ll ans[10];//用来储存每个数码出现的次数 
ll bin[15];//表示i位数中数码i出现的次数 
ll d[15];//这个用来存储数的每一位 
void rule(){
    bin[1]=1;
    for(int i=2;i<14;i++) bin[i]=bin[i-1]*10;
    for(int i=0;i<10;i++) dp[1][i][i]=1;
    for(int i=2;i<=13;i++){
        for(int j=0;j<=9;j++){
            for(int z=0;z<=9;z++){
                for(int k=0;k<=9;k++)
                dp[i][j][z]+=dp[i-1][k][z];//比如i=2,j=2时，所求数字范围应该是200-299,这一步把0-99中各数码出现次数加进去 
                dp[i][z][z]+=bin[i-1];//这一位这是把200-299总共出现了100次的2给加进去 
            }
        }
    }
}
void solve(ll x,int flag){
    ll tmpx=x;//存储传进来的x 
    int cnt=0;//记录x的位数 
    memset(d,0,sizeof(d));
    while(x){
        d[++cnt]=x%10;
        x/=10;
    }
    for(int i=1;i<cnt;i++){//这一步是最高位为0的，这些数都不会受到x的上限限制，都可以直接加进来 
        for(int j=1;j<=9;j++){
            for(int k=0;k<=9;k++)
            ans[k]+=dp[i][j][k]*flag;
        }
    }
    int tmpt=cnt;
    while(cnt){//可以举个456的例子来仔细分析一下 
        for(int i=0;i<d[cnt];i++){//注意这里是小于不是等于，保证上限不被取到，在后面再被处理 
            if(!i&&cnt==tmpt) continue;//这种情况在最高位为0时已经统计过了，不能重复 
            for(int j=0;j<=9;j++){
                    ans[j]+=dp[cnt][i][j]*flag;//不是上限的时候都直接加 
            }
        }
        ans[d[cnt]]+=(tmpx%bin[cnt]+1)*flag;cnt--;//随着while循环，上限一步步的被处理 
    }//简述一下过程（456），就是第一个for处理了0-399，然后把首位4的57次加上，第二个for，处理的0-49......就这样一步步往下 
}
int  main(){  
  ll a,b;scanf("%lld%lld",&a,&b);
  rule();
  solve(b,1);solve(a-1,-1);//1和-1是符号位，分别是加和减 
  for(int i=0;i<10;i++)
  printf("%lld%c",ans[i],i==9?'\n':' ');    
  return 0;
}