AVL树
AVL树又称为高度的平衡二叉树,它能保持二叉树高度的平衡,尽量降低二叉树的高度,较少树的平均搜索长度。如下是二叉搜索树比较极端的一种情况,这使得二叉搜索树效率降低。而AVL树就是为了解决这一问题。
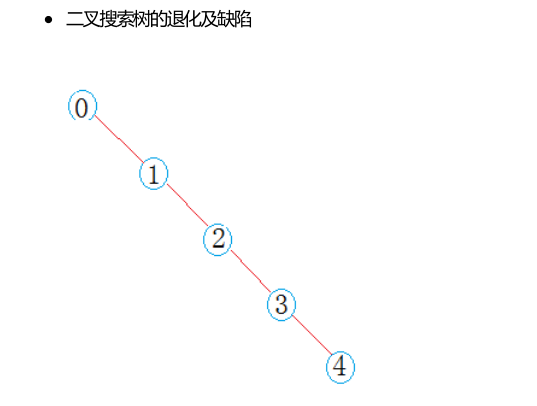
AVL树有哪些性质呢?首先它的左子树和有字数的高度差不超过1,并且它的左子树和右子树都要是AVL树才可以。
下面是AVL树的插入过程,其他操作与插入过程类似,因此不再赘述。
template<class K,class V>
struct AVLNode //AVL树的节点,三叉链的结构方便节点找他的父节点
{
K _key;
V _value;
AVLNode<K, V>* _left;
AVLNode<K, V>* _right;
AVLNode<K, V>* _parent;
int _bf; //平衡因子
AVLNode(const K&key, const V& value)
:_key(key)
, _value(value)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
, _bf(0)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLNode<K, V> Node;
public:
AVLTree()
:_root(NULL)
{}
~AVLTree()
{
Destory(_root);
}
void Destory(Node* root)
{
if (root == NULL)
return;
Destory(root->_left);
Destory(root->_right);
delete root;
}
bool Insert(const K& key,const V&value) //插入节点
{
if (_root == NULL)
{
_root = new Node(key,value);
return true;
}
Node* cur = _root;
Node* parent = NULL;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key,value);
if (parent->_key < key)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
while (parent) //调整平衡因子
{
if (parent->_left == cur) //在左边插入节点,平衡因子减一(平衡因子的值为右子树高度减左子树高度)
{
parent->_bf--;
}
else //在右边插入节点,平衡因子加一
{
parent->_bf++;
}
if (parent->_bf == 0) //如果节点的平衡因子等于0,说明二叉树不需要调整
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) //如果平衡因子等于1或-1,则需要继续向上调整
{
cur = parent;
parent = cur->_parent;
}
else //parent->_bf==2 //如果平衡因子的绝对值大于1则需要对树进项旋转操作,旋转分为四种情况
{
if (parent->_bf == 2)
{
if (cur->_bf == 1)
{
RotateL(parent);
}
else //cur->_bf==-1
{
RotateRL(parent);
}
}
else //parent->_bf==-2
{
if (cur->_bf == 1)
{
RotateLR(parent);
}
else //cur->_bf==-1
{
RotateR(parent);
}
}
break;
}
}
return true;
}
void RotateL(Node* parent) //左旋
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
subR->_left = parent;
if (subRL)
subRL->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if (ppNode == NULL)
{
_root = subR;
subR->_parent == NULL;
}
else
{
if (ppNode->_left == parent)
ppNode->_left = subR;
else
ppNode->_right = subR;
subR->_parent = ppNode;
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent) //右旋
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left=subLR ;
subL->_right = parent;
if (subLR)
subLR->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
if (ppNode == NULL)
{
_root = subL;
subL->_parent = NULL;
}
else
{
if (ppNode->_left ==parent)
ppNode->_left = subL;
else
ppNode->_right = subL;
subL->_parent = ppNode;
}
subL->_bf = parent->_bf = 0;
}
void RotateLR(Node* parent) //左右双旋
{
RotateL(parent->_left);
RotateR(parent);
}
void RotateRL(Node* parent) //右左双旋
{
RotateR(parent->_right);
RotateL(parent);
}
private:
Node* _root;
};
struct AVLNode //AVL树的节点,三叉链的结构方便节点找他的父节点
{
K _key;
V _value;
AVLNode<K, V>* _left;
AVLNode<K, V>* _right;
AVLNode<K, V>* _parent;
int _bf; //平衡因子
AVLNode(const K&key, const V& value)
:_key(key)
, _value(value)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
, _bf(0)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLNode<K, V> Node;
public:
AVLTree()
:_root(NULL)
{}
~AVLTree()
{
Destory(_root);
}
void Destory(Node* root)
{
if (root == NULL)
return;
Destory(root->_left);
Destory(root->_right);
delete root;
}
bool Insert(const K& key,const V&value) //插入节点
{
if (_root == NULL)
{
_root = new Node(key,value);
return true;
}
Node* cur = _root;
Node* parent = NULL;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key,value);
if (parent->_key < key)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
while (parent) //调整平衡因子
{
if (parent->_left == cur) //在左边插入节点,平衡因子减一(平衡因子的值为右子树高度减左子树高度)
{
parent->_bf--;
}
else //在右边插入节点,平衡因子加一
{
parent->_bf++;
}
if (parent->_bf == 0) //如果节点的平衡因子等于0,说明二叉树不需要调整
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) //如果平衡因子等于1或-1,则需要继续向上调整
{
cur = parent;
parent = cur->_parent;
}
else //parent->_bf==2 //如果平衡因子的绝对值大于1则需要对树进项旋转操作,旋转分为四种情况
{
if (parent->_bf == 2)
{
if (cur->_bf == 1)
{
RotateL(parent);
}
else //cur->_bf==-1
{
RotateRL(parent);
}
}
else //parent->_bf==-2
{
if (cur->_bf == 1)
{
RotateLR(parent);
}
else //cur->_bf==-1
{
RotateR(parent);
}
}
break;
}
}
return true;
}
void RotateL(Node* parent) //左旋
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
subR->_left = parent;
if (subRL)
subRL->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if (ppNode == NULL)
{
_root = subR;
subR->_parent == NULL;
}
else
{
if (ppNode->_left == parent)
ppNode->_left = subR;
else
ppNode->_right = subR;
subR->_parent = ppNode;
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent) //右旋
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left=subLR ;
subL->_right = parent;
if (subLR)
subLR->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
if (ppNode == NULL)
{
_root = subL;
subL->_parent = NULL;
}
else
{
if (ppNode->_left ==parent)
ppNode->_left = subL;
else
ppNode->_right = subL;
subL->_parent = ppNode;
}
subL->_bf = parent->_bf = 0;
}
void RotateLR(Node* parent) //左右双旋
{
RotateL(parent->_left);
RotateR(parent);
}
void RotateRL(Node* parent) //右左双旋
{
RotateR(parent->_right);
RotateL(parent);
}
private:
Node* _root;
};



