数据结构之堆栈

因为找工作的原因，发现自己的数据结构和算法太薄弱了，被虐的很惨，遂下定决心开始从头学习数据结构和算法，就在MOOC上找了一门浙江大学开设的数据结构课程，也特地开了博客来记录一下此次学习之旅，也在这里定下一个目标，希望能够坚持到底，奥利给！！

什么是堆栈

首先从一个非常经典的算术表达式求解问题开始堆栈的学习。

5 + 6 / 2 - 3 * 4

如何求解上面的表达式？

1、表达式由两类对象构成：运算数和运算符号

2、不同的运算符号有不同的优先级

一般，我们见到的算术表达式称为中缀表达式，因为运算符号位于两个运算数之间，如 a + b * c - d / e。

为了方便计算机计算，我们一般将中缀表达式转换为后缀表达式：如a b c * + d e / -.

如何将中缀表达式转换为后缀表达式

需要借助堆栈来实现，按照我们计算表达式的流程，我们从左往右扫描表达式，并用堆栈来记录运算符号，当我们遇到一个运算符号小于先前记录的运算符序列的最后一个时（同优先级符号的从左往右优先级递减），这就表明我们应该事先运算前面的子表达式，所以将堆栈里的运算符弹出，直到在堆栈里遇到的运算符小于当前的预算符号。带括号的表达式中，左括号在堆栈外时，优先级为最高，当在堆栈里时，优先级最低。所以在扫描表达式时遇到左括号直接入入栈，遇到右括号后，开始弹出堆栈里的运算符，直到遇到左括号后，左括号弹出，因为括号优先级最低，所以此时运算符堆栈应该会出清。

转换规则：

 从头到尾读取中缀表达式的每个对象，对不同对象按不同的情况处理。

① 运算数：直接输出；

② 左括号：压入堆栈；

③ 右括号：表达括号内的中缀表达式已经扫描完毕，将栈顶的运算符弹出并输出，直到遇到左括号（出栈，不输出）；

④ 运算符：

• 若优先级大于栈顶运算符时，则把它压栈；

• 若优先级小于等于栈顶运算符时，将栈顶运算符弹出并输出；再比较新的栈顶运算符，直到该运算符大于栈顶运算符优先级为止，然后将该运算符压栈；

⑤ 若各对象处理完毕，则把堆栈中存留的运算符一并输出。

 

 

 

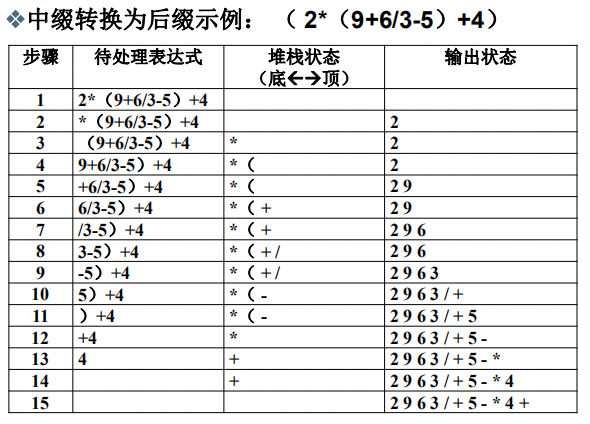
这样，我们就完成了从中缀表达式到后缀表达式的转换，接下来，我们可以对该后缀表达式进行求值运算。

后缀表达式的求值策略：

1、首先我们知道，后缀表达式已经将预算符号的优先级和预算数进行了一定的排列，所以我们可以重做往右扫描，逐个处理运算符和运算数。

遇到预算数时：压入堆栈存储，达到记住未参与运算数的目的

遇到预算符号时：将栈里的运算数取出和运算符做运算，然后将运算结果入栈存储

直到扫描到表达式的最末端，结束搜索，做完运算后，栈应该是空的。

贴上我自己的实现：

/**  求后缀表达式  ***/

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define MAX_SIZE 1000
typedef char ElementType;

typedef struct t_stack
{
    ElementType data[MAX_SIZE];
    int top;
}Stack_t;
typedef Stack_t * pStack;

typedef struct t_dstack
{
    ElementType StackBuf[MAX_SIZE];
    int top1;
    int top2;
}DStack_t;

pStack stack_New(void)
{
    pStack NewStack = (pStack)malloc(sizeof(Stack_t));
    memset(NewStack->data, 0, sizeof(NewStack->data));
    NewStack->top = -1;
    return NewStack;
}

/* 堆栈存储运算发符号 */
pStack stack = NULL;
char tempResult[100] = {0};
int charNum = 0;

int stack_isEmpty(Stack_t *s)
{
    if (s)
    {
        if (s->top == -1)
            return 1;
        else
            return 0;
    }
    else
        return 1;
    
}

ElementType pop(pStack s)
{
    if (!stack_isEmpty(s))
    {
        return s->data[(s->top)--];
    }
}

void push(pStack s, ElementType x)
{
    if (s && s->top != MAX_SIZE - 1)
    {
        s->data[++(s->top)] = x;
    }
}

ElementType stack_gettop(pStack s)
{
    if (!stack_isEmpty(s))
    {
        return s->data[(s->top)];
    }
    else
    {
        return -1;
    }
    
}


int tokenLevel(char token)
{
    int level = 0;
    if (token == '*' || token == '/')
    {
        level = 1;
    }
    else if (token == '(')
    {
        level = -1;
    }
    
    return level;
}

int tokenCmp(char checktoken)
{
    int ret = 0;
    char toptoken = stack_gettop(stack);
    int checklevel = tokenLevel(checktoken);
    int stacklevel = tokenLevel(toptoken);
    if (checktoken == ')' && toptoken == '(')
    {
        pop(stack);
        return 0;
    }
    if (toptoken == -1)
    {
        /* 空栈直接压入操作符号 */
        push(stack, checktoken);
        return 0;
    }
    else if (checklevel <= stacklevel || checktoken == ')')
    {
        /* 弹出堆栈内的运算符 */
        tempResult[charNum++] = pop(stack);
        tokenCmp(checktoken);
    }
    else
    {
        push(stack, checktoken);
        return 0;
    }
    return ret;
}

int main(void)
{
    char expressString [100] = {0};
    stack = stack_New();
    int ret = 0;
    while (scanf("%s", expressString) != EOF)
    {
        int i = 0;
        memset(tempResult, 0, sizeof(tempResult));
        charNum = 0;
        
        while (expressString[i] != '\0')
        {
            if ((expressString[i]) >= '0' && expressString[i] <= '9')
            {
                tempResult[charNum] = expressString[i];
                charNum++;
            }
            else if (expressString[i] == '(')
            {
                push(stack, expressString[i]);
            }
            else
            {
                if (stack_isEmpty(stack))
                {
                    push(stack, expressString[i]);
                }
                else
                {
                    tokenCmp(expressString[i]);
                }
            }
            i++;
        }
        while (!stack_isEmpty(stack))
        {
            tempResult[charNum++] = pop(stack);
        }
        /* 利用堆栈计算值 */
        stack->top = -1;
        for (i = 0; i < charNum; i++)
        {
            if (tempResult[i] >= '0' && tempResult[i]<= '9')
                push(stack, tempResult[i]-'0');
            else
            {
                int a = pop(stack);
                int b = pop(stack);
                switch (tempResult[i])
                {
                    case '+':
                        ret = a + b;
                        push(stack, ret);
                        break;
                    case '-':
                        ret = b - a;
                        push(stack,ret);
                        break;
                    case '*':
                        ret = a * b;
                        push(stack,ret);
                        break;
                    case '/':
                        if (b)
                            ret = b / a;
                        push(stack,ret);
                        break;
                    default:
                        break;
                }
            }
            
        }
        printf("%d", ret);
        memset(expressString, 0, sizeof(expressString));
    }

}

 

栈的特性：

只在一端（栈顶，Top）做 插入、删除

 插入数据：入栈（Push）

 删除数据：出栈（Pop）

 后入先出：Last In First Out（LIFO）

 

栈的其他应用

1、函数调用和递归实现

2、深度优先搜索

3、回溯算法

。。。

堆栈的抽象数据类型描述

类型名称: 堆栈（Stack）

数据对象集：一个有0个或多个元素的有穷线性表。

操作集：长度为MaxSize的堆栈S - Stack，堆栈元素item - ElementType

1、Stack CreateStack( int MaxSize )： 生成空堆栈，其最大长度为MaxSize；

2、int IsFull( Stack S, int MaxSize )：判断堆栈S是否已满；

3、void Push( Stack S, ElementType item )：将元素item压入堆栈；

4、int IsEmpty ( Stack S )：判断堆栈S是否为空；

5、ElementType Pop( Stack S )：删除并返回栈顶元素；

基于数组的栈实现