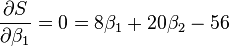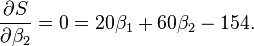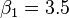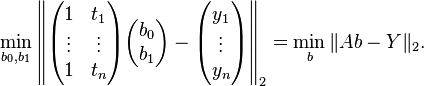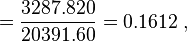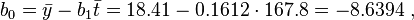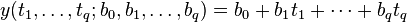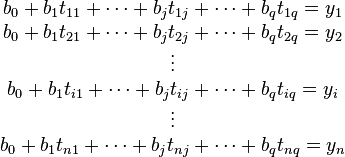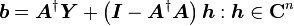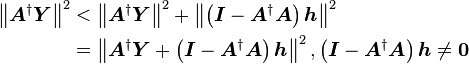最小二乘法
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。

某次实验得到了四个数据点  :
: 、
、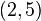 、
、 、
、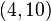 (右图中红色的点)。我们希望找出一条和这四个点最匹配的直线
(右图中红色的点)。我们希望找出一条和这四个点最匹配的直线 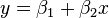 ,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的
,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的  和
和 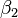 :
:
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值:
最小值可以通过对 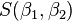 分别求
分别求  和
和 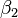 的偏导数,然后使它们等于零得到。
的偏导数,然后使它们等于零得到。
如此就得到了一个只有两个未知数的方程组,很容易就可以解出:
也就是说直线  是最佳的。
是最佳的。
简介[编辑]
1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中,而法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为时人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,见高斯-马尔可夫定理。
方法[编辑]
人们对由某一变量 或多个变量
或多个变量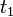 ……
……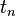 构成的相关变量
构成的相关变量 感兴趣。如弹簧的形变与所用的力相关,一个企业的盈利与其营业额,投资收益和原始资本有关。为了得到这些变量同
感兴趣。如弹簧的形变与所用的力相关,一个企业的盈利与其营业额,投资收益和原始资本有关。为了得到这些变量同 之间的关系,便用不相关变量去构建
之间的关系,便用不相关变量去构建 ,使用如下函数模型
,使用如下函数模型
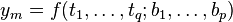 ,
,
 个独立变量或
个独立变量或 个系数去拟合。
个系数去拟合。
通常人们将一个可能的、对不相关变量t的构成都无困难的函数类型称作函数模型(如抛物线函数或指数函数)。参数b是为了使所选择的函数模型同观测值y相匹配。(如在测量弹簧形变时,必须将所用的力与弹簧的膨胀系数联系起来)。其目标是合适地选择参数,使函数模型最好的拟合观测值。一般情况下,观测值远多于所选择的参数。
其次的问题是怎样判断不同拟合的质量。高斯和勒让德的方法是,假设测量误差的平均值为0。令每一个测量误差对应一个变量并与其它测量误差不相关(随机无关)。人们假设,在测量误差中绝对不含系统误差,它们应该是纯偶然误差(有固定的变异数),围绕真值波动。除此之外,测量误差符合正态分布,这保证了偏差值在最后的结果y上忽略不计。
确定拟合的标准应该被重视,并小心选择,较大误差的测量值应被赋予较小的权。并建立如下规则:被选择的参数,应该使算出的函数曲线与观测值之差的平方和最小。用函数表示为:

用欧几里得度量表达为:

最小化问题的精度,依赖于所选择的函数模型。
线性函数模型[编辑]
典型的一类函数模型是线性函数模型。最简单的线性式是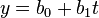 ,写成矩阵式,为
,写成矩阵式,为
直接给出该式的参数解:
 和
和 
其中 ,为t值的算术平均值。也可解得如下形式:
,为t值的算术平均值。也可解得如下形式:
简单线性模型 y = b0 + b1t 的例子[编辑]
随机选定10艘战舰,并分析它们的长度与宽度,寻找它们长度与宽度之间的关系。由下面的描点图可以直观地看出,一艘战舰的长度(t)与宽度(y)基本呈线性关系。散点图如下:
以下图表列出了各战舰的数据,随后步骤是采用最小二乘法确定两变量间的线性关系。
| 编号 | 长度 (m) | 宽度 (m) | ti - t | yi - y | |||
|---|---|---|---|---|---|---|---|
| i | ti | yi | ti* | yi* | ti*yi* | ti*ti* | yi*yi* |
| 1 | 208 | 21.6 | 40.2 | 3.19 | 128.238 | 1616.04 | 10.1761 |
| 2 | 152 | 15.5 | -15.8 | -2.91 | 45.978 | 249.64 | 8.4681 |
| 3 | 113 | 10.4 | -54.8 | -8.01 | 438.948 | 3003.04 | 64.1601 |
| 4 | 227 | 31.0 | 59.2 | 12.59 | 745.328 | 3504.64 | 158.5081 |
| 5 | 137 | 13.0 | -30.8 | -5.41 | 166.628 | 948.64 | 29.2681 |
| 6 | 238 | 32.4 | 70.2 | 13.99 | 982.098 | 4928.04 | 195.7201 |
| 7 | 178 | 19.0 | 10.2 | 0.59 | 6.018 | 104.04 | 0.3481 |
| 8 | 104 | 10.4 | -63.8 | -8.01 | 511.038 | 4070.44 | 64.1601 |
| 9 | 191 | 19.0 | 23.2 | 0.59 | 13.688 | 538.24 | 0.3481 |
| 10 | 130 | 11.8 | -37.8 | -6.61 | 249.858 | 1428.84 | 43.6921 |
| 总和(Σ) | 1678 | 184.1 | 0.0 | 0.00 | 3287.820 | 20391.60 | 574.8490 |
仿照上面给出的例子
 并得到相应的
并得到相应的 .
.
然后确定b1
可以看出,战舰的长度每变化1m,相对应的宽度便要变化16cm。并由下式得到常数项b0:
在这里随机理论不加阐述。可以看出点的拟合非常好,长度和宽度的相关性大约为96.03%。 利用Matlab得到拟合直线: 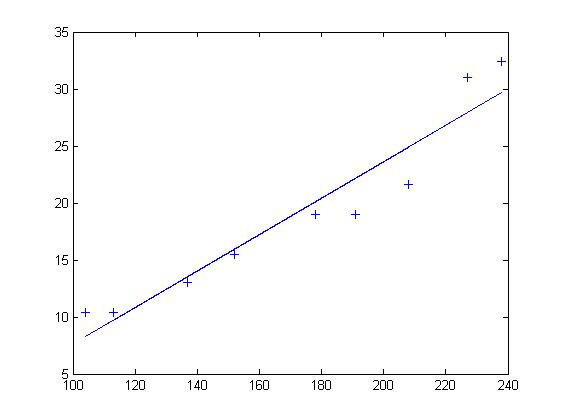
一般线性情况[编辑]
若含有更多不相关模型变量 ,可如组成线性函数的形式
,可如组成线性函数的形式
通常人们将tij记作数据矩阵 A,参数bj记做参数向量b,观测值yi记作Y,则线性方程组又可写成:
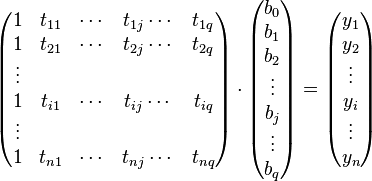 即
即 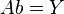
上述方程运用最小二乘法导出为线性平方差计算的形式为:
 。
。
最小二乘法的解[编辑]
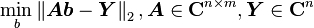
的特解为A的广义逆矩阵与Y的乘积,这同时也是二范数极小的解,其通解为特解加上A的零空间。证明如下:
先将Y拆成A的值域及其正交补两部分
所以 ,可得
,可得
故当且仅当 是
是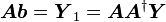 解时,
解时, 即为最小二乘解,即
即为最小二乘解,即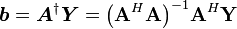 。
。
又因为
故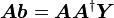 的通解为
的通解为
因为
所以 又是二范数极小的最小二乘解。
又是二范数极小的最小二乘解。



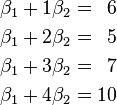
![\begin{align}
S(\beta_1, \beta_2) =
&\left[6-(\beta_1+1\beta_2)\right]^2+\left[5-(\beta_1+2\beta_2) \right]^2 \\
&+\left[7-(\beta_1 + 3\beta_2)\right]^2+\left[10-(\beta_1 + 4\beta_2)\right]^2.\\
\end{align}](http://upload.wikimedia.org/math/a/2/1/a21abd8e36caa43fcfd6dedbbaac4af1.png)