Matlab绘制信号包络线

Matlab绘制包络线可以通过hilbert或者envelope实现，先说hilbert

---

Hilbert 变换

 

Hilbert 变换可用于形成解析信号。解析信号在通信领域中很有用，尤其是在带通信号处理中。工具箱函数 hilbert 计算实数输入序列 x 的 Hilbert 变换，并返回相同长度的复数结果，即 y = hilbert(x)，其中 y 的实部是原始实数数据，虚部是实际 Hilbert 变换。在涉及到连续时间解析信号时，y 有时被称为解析信号。离散时间解析信号的关键属性是它的 Z 变换在单位圆的下半部分为 0。解析信号的许多应用都与此属性相关；例如，用解析信号避免带通采样操作的混叠效应。解析信号的幅值是原始信号的复包络。

%% 基本参数
A = 1; % 激励信号幅值
N = 15; % cycle数，即激励信号波峰数
fck = 100; % 激励中心频率 kHz
fc = 100e3; % 激励信号中心频率，Hz
T0 = 1e-4; % 导波传播时间
T = 4.0*T0; % 激励持续时长
dt = 1/(20*fc)/2; % 时间步长，在最大步长基础上除以2
t = [0:dt:T]'; % 时间序列
V = A*[heaviside(t)-heaviside(t-N/fc)].*(1-cos(2*pi*fc*t/N)).*sin(2*pi*fc*t);
h = hilbert(V); % Hilbert变换
figure
plot(t,V)

　　

 

 

 

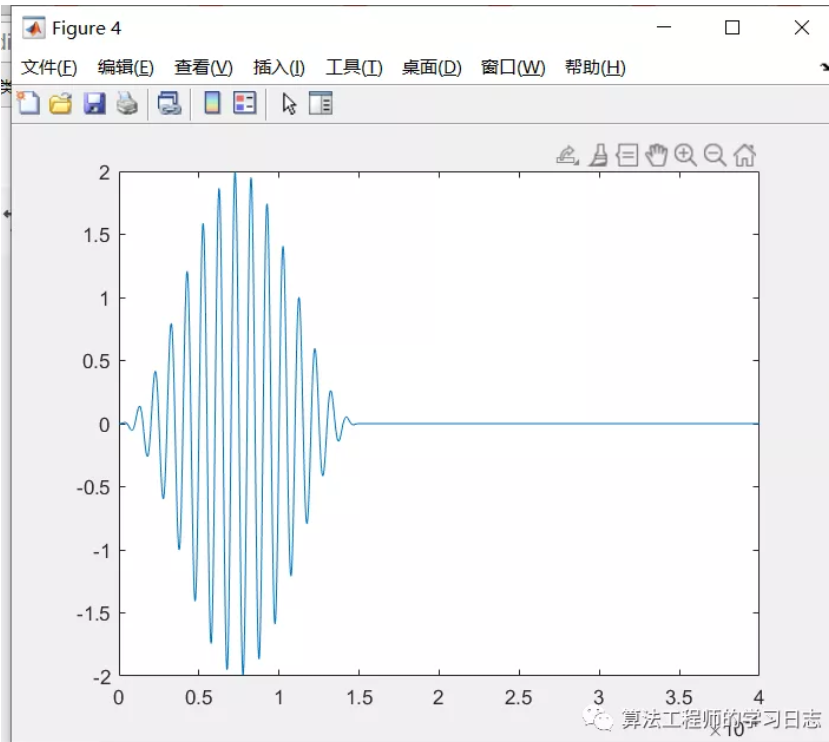
%% 包络绘制
figure
plot(t,V)
hold on
plot(t,abs(h),'--','linewidth',1.5)
hold on
plot(t,-1*abs(h),'-.','linewidth',1.5)
grid on

　　

 

 

 

---

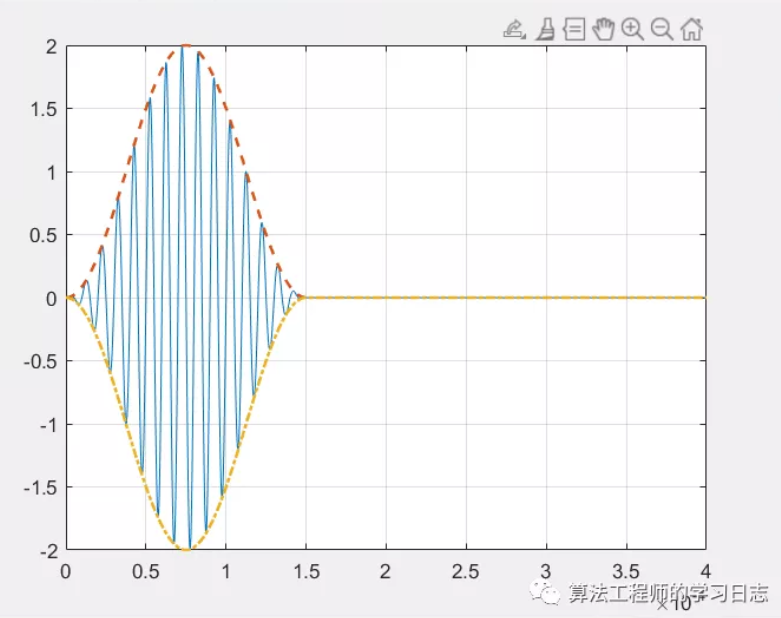
envelope

envelope返回输入序列x的上下包络线，作为其解析信号的大小。x的解析信号是利用希尔伯特实现的离散傅里叶变换得到的。这个函数首先移除x的均值，然后在计算包络线之后再把它加回来。如果x是一个矩阵，那么包络线对x的每一列都是独立的。

% 信号生成
t = 0:1/2000:2-1/2000;
q = chirp(t-2,4,1/2,6,'quadratic',100,'convex').*exp(-4*(t-1).^2);
plot(t,q)

　　

 

 

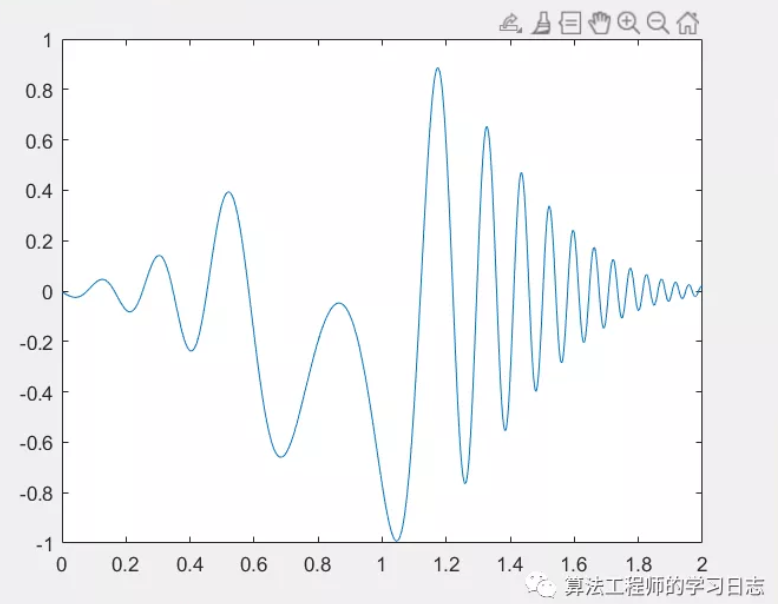
% 包络线绘制
[up,lo] = envelope(q);
figure
plot(t,q)
hold on
plot(t,up,t,lo,'linewidth',1.5)
legend('signal','上包络线','下包络线')
hold off