约瑟夫环问题的递推和递归求解
约瑟夫环问题的递推和递归求解
说道约瑟夫环问题大家一定不会陌生,本科时学数据结构应该都有学过。最容易想到的接替思路就是用链表模拟这个过程(实际上,我用的教材,也是在链表这一章引入的约瑟夫环问题)。
但是模拟求解的方式比较麻烦,效率也低,而且操作链表,一不小心就会出错。
我们可以考虑用数学推导的方式求解,这种方法只要理解推导过程,写出推导表达式就可以求解了。下面详细来说。
给出递推式,并验证其正确性
首先说明,我不会证明这个递推公式,我只是验证一下这个公式。
直接给出递推公式。
f(m,k,i) = ( f(m-1,k,i-1) + k ) % m;
其中m的含义是,有m个人
k的含义是,数到k的人出列
i的含义是,第i个出列
所以f(m,k,i)就是求:
m个人围成一个环,编号为0------m-1,从编号为0的人开始报数,报道k的人出列,第i个出列的人的编号。
该递推式的含义就是:
如果已知m-1个人围成的约瑟夫环中,第i-1个出列的人的编号,假设为temp,那么我们就可以求出m个人围成的约瑟夫环中,第i个出列的人的编号,为: (temp + k) % m
也可以理解成递归式,含义是:
要想求,m个人围成的约瑟夫环中,第i个出列的人的编号,就要先求m-1个人围成的约瑟夫环中,第i-1个出列的人的编号。
我们简单验证一下:
我们先自己分别求出:
8个人的约瑟夫环依次出列的人的编号(从1报数到3)
9个人的约瑟夫环依次出列的人的编号(从1报数到3)
10个人的约瑟夫环依次出列的人的编号(从1报数到3)
如下图所示。
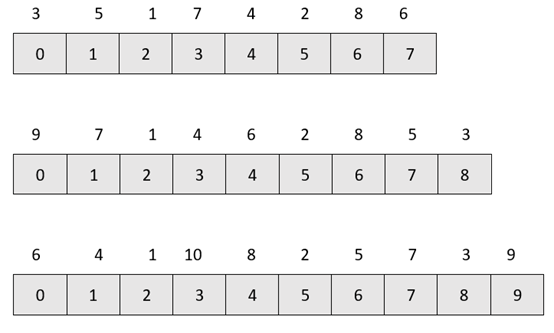
上面的数字表示对应的编号出列的顺序。
如果我们把编号按照出列的顺序重新拍一下就是下面的效果:
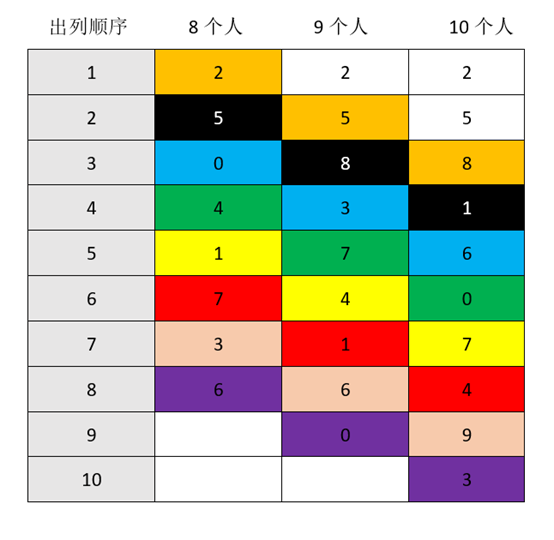
然后我们观察,对角线上(相同颜色的三个)的三个数是否满足递推公式。答案是肯定的。
比如说:
8个人的环中,第6个出列的编号是7
9个人的环中,第7个出列的编号是(7+3)%9 = 1(其中m=9,k=3)
10个人的环,第8个出列的编号是(1+3)%10=4(其中m=10,k=3)
验证其他的也是一样,完全正确。
验证了递归式(递推式)的正确性,下面我们开始想代码怎么写。
递归比较简单,通过上图我们可以看到,求第一出列的人的编号,是没有办法用递推公式的,也就是第一个出列的人的编号必须我们自己求,当然这也简单,这个同时也就作为递归出口。
递推可能要多想一下,比如我们要求10个人的环中第3个出列的编号,我们就先要求出8个人的环中,第1个出列的编号,然后再利用递推式递推求解。
如果是求m个人的环中第i个出列的人的编号,我们就先要求出
m-(i-1)个人的环,也就是m-i+1个人的环中,第1个出列的编号,然后再利用递推式递推求解。
下面给出代码。
#include <stdio.h> #include <stdlib.h> /** * 递推方式求解 * @para * m表示有m个人 * k表示数到k的人出列 * i表示第i个出列 * @return * 返回值就表示,一个m个人(0---m-1)组成的环,从编号为0的人开始数1,数到k出列 * 这样第i个出列的人的编号是多少 * 如果编号是(1-----m)那就再最终的结果上加1即可 * * */ int joes1(int m,int k,int i) { int start = m - i + 1; int temp = (start + k - 1)%start;//如果不是从编号为0的人开始报数,那只需修改这里即可,不需要修改递推式 int j = 0; for(j = 1;j < i;j++) { temp = (temp + k)%(start + j);//递推式 } return temp; } int joes2(int m,int k,int i) { if(i == 1) { return (m + k - 1)%m;//如果不是从编号为0的人开始报数,那只需要修改递归出口即可,不需要修改递归式 } else { return (joes2(m-1, k, i-1) + k)%m; } } int main() { int m,k,i; scanf("%d %d %d",&m,&k,&i); printf("%d个人中,第%d个出队的是%d\n",m,i,joes1(m,k,i)); printf("%d个人中,第%d个出队的是%d\n",m,i,joes2(m,k,i)); return 0; }
如果编号从1开始怎么办?
约瑟夫环的问题,我们都转换成编号从0开始,如果编号从1开始那么我们就只需在最后结果上加上1即可。
如果不从第一个人开始报数怎么办?
不管从第几个人开始报数,递推式(递归式)都是成立的,我们只需修改求初始值的表达式(递归出口的表达式)即可。
如果你觉得对你有用,请赞一个吧~~~




