选择排序之简单选择排序和堆排序
选择排序之简单选择排序和堆排序
选择排序的思想非常直接,不是要排序么?那好,我就从所有序列中先找到最小的,然后放到第一个位置。之后再看剩余元素中最小的,放到第二个位置……以此类推,就可以完成整个的排序工作了。可以很清楚的发现,选择排序是固定位置,找元素。相比于插入排序的固定元素找位置,是两种思维方式。
常见的选择排序有:简单选择排序和堆排序。
简单选择排序
简单选择排序的思想是,从第一位置开始,逐渐向后,选择后面的无序序列中的最小值放到该位置。很简单,直接上代码吧:
#include <stdio.h> #include <stdbool.h> void select_sort(int value[],int n) { int i = 0; for(i = 0;i < n - 1;i++) { int j = i; int min_index = i;//记录最小值的下标 for(j = i + 1;j < n;j++) { if(value[j] < value[min_index]) { min_index = j; } } if(min_index != i)//将最小值放在正确的位置 { int temp = value[i]; value[i] = value[min_index]; value[min_index] = temp; } } } int main() { int value[] = {8,6,3,7,4,5,1,2,10,9}; int n = 10; select_sort(value,n); printf("排序结果为:\n"); int i = 0; for(;i < n;i++) { printf("%d ",value[i]); } printf("\n"); return 0; }
直接选择排序和冒泡排序很像,不同的是冒泡排序要比较每两个相邻的元素并且交换(如果需要),而直接选择排序则只需要将选择出来的最小值与它应该所在的位置上的数进行交换即可。在这里也给出冒泡排序的代码:
#include <stdio.h> #include <string.h> #include <stdlib.h> #include <stdbool.h> void bubble_sort(int value[],int n) { int i = 0; for(;i < n - 1;i++)//n-1趟 { int j = 0; bool tag = false; for(;j < n-i-1;j++)//依次进行两两比较 { if(value[j] > value[j+1]) { tag = true;//存在交换 int temp = value[j]; value[j] = value[j + 1]; value[j + 1] = temp; } } if(!tag)//不存在交换,说明已经有序,退出循环 break; } printf("进行了%d趟排序\n",i); } int main() { int value[] = {8,6,3,7,4,5,1,2,10,9}; int n = 10; bubble_sort(value,n); printf("排序结果为:\n"); int i = 0; for(;i < n;i++) { printf("%d ",value[i]); } printf("\n"); return 0; }
通过比较冒泡排序和简单选择排序的代码就可以看到,两者的比较操作都是在内层循环中进行的,比较操作的时间复杂度都是O(n2)。但是对于交换操作,冒泡排序是在内层循环,而简单选择排序是在外层循环中,所以对于交换操作,冒泡排序最好的情况是0次,最差的情况是n(n-1)/2(大概呀),简单选择排序的最好情况是0次,最差情况是n-1次。所以简单选择排序的效率要高于冒泡排序。
堆排序
堆的定义

若将和此序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。
排序时我们通常使用大顶堆,小顶堆主要用于优先队列。
对于一棵满二叉树或者完全二叉树,我们可以用线性存储结构(数组)来进行存储。
比如对于完全二叉树:

可以用数组:[0,1,2,3,4,5,6,7,8,9]来表示,节点之间的父子关系是:对于i节点,左孩子为2i+1,右孩子为2i+2.比如对于0号节点,他的孩子就是2*0+1=1,和2*0+2=2。所以用数组就可以表示完全二叉树。之所以我们平时用链式结构表示二叉树,是因为,如果二叉树不是完全二叉树,那么如果用数组表示,我们就必须为空节点留出存储位置。比如:如果上图没有2号节点和其子节点,如果我们仍用数组存储,我们依然需要长度为10的数组来表示这棵树,否则节点和其子节点之间2i+1的关系就会破坏,也就没有了节点之间的关系。这造成了存储空间的浪费。
调整操作
对于完全二叉树:
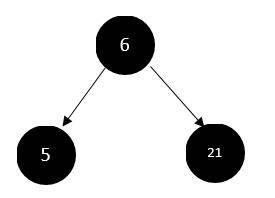
显然不满足大顶堆的定义,那我们怎么调整,使其满足大顶堆的条件呢?
很简单,就是找出6、5、21(也就是本节点和它的两个孩子之间)三者之间的最大值,也就是21,然后交换6和21(也就是本节点和最大节点)即可。如下图:
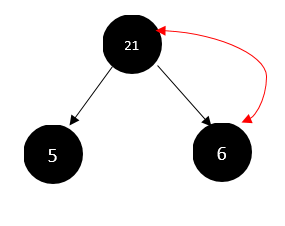
顶元素筛下操作
对于一个满足大顶堆的完全二叉树来说,树根就是最大的元素,而我们排序,最大的元素应当放在数组的最后,所以我们要将最后一个元素的树根元素进行交换,将树根元素放在最后,这样该元素就到了它应该在的位置。这个过程叫做顶元素筛下。如果我们反复进行顶元素筛下操作,那么最大值就会依次被放在正确的位置,也就完成了排序工作。但是要注意的是,没筛选一个顶元素,就会使原有二叉树不再满足大顶堆的定义,这时候要进行调整。比如:
有大顶堆:
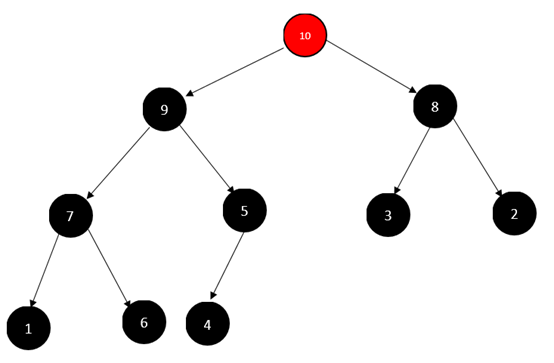
这是后,根元素10,为最大元素,我们进行顶元素筛下,也就是将最后一个元素4和10进行交换
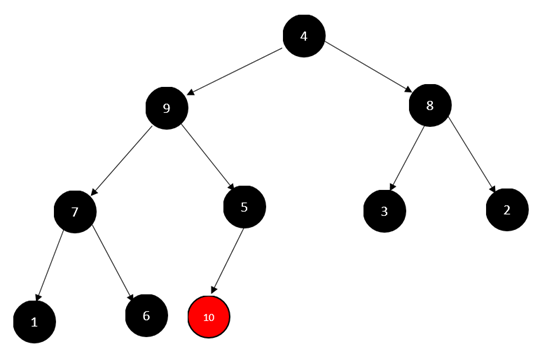
这个时候10就到了正确的位置。但是我们发现完全二叉树已经不满足大顶堆了!这个时候要进行调整(注意,此时,调整的二叉树应该是除了10以外的,因为10是刚刚筛下的,而且已经在正确的位置上了)。调整要从根节点开始:

此时我们发现,虽然9、4、8三个节点满足了大顶堆。但是由于4和9的交换,导致4、7、5不满足大顶堆,因此还要继续调整,调整到什么时候呢?调整到叶子节点!(注意调整时已经不包括10这个节点了,所以5这个节点现在就是叶子节点了)。
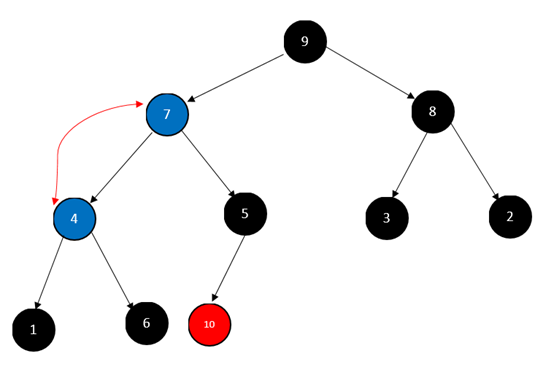
此时已经到了最后一个非叶子节点,再次进行调整(如果需要)后,整棵树就满足大顶堆了。

调整完后,我们就要进行下一轮顶元素筛下和调整了。

接下来就不写了。
总结一下就是,对于已经创建好的大顶堆,我们进行顶元素筛下操作,也就是将顶元素和最后一个元素进行交换,然后从顶元素开始,沿着交换路径进行调整,直到叶子节点,整棵树就满足大顶堆了。然后就可以进行下一轮筛下了,反复进行,就可以达到排序的目的。需要注意的是,调整的过程,针对的二叉树是不包含已经筛下的节点的,还要注意最后一个非叶子节点很可能没有右孩子节点,这一点编程的时候要进行判断,因为实际数组中那个位置很可能是我们刚刚筛下的那个元素,而调整时,是不包括已经筛下的元素的!!
建立大顶堆
利用顶元素筛下操作进行排序,前提是我们要先建立一个大顶堆。大顶堆的建立实际上也是一个类似顶元素筛下的调整过程,所不同的是,顶元素筛下的调整是对根元素来一次直到叶子节点的调整,而创建堆的过程是从最后一个非叶子节点到根节点,对这其中所有的节点都进行一次直到叶子节点的调整(如果需要)。
比如有完全二叉树:
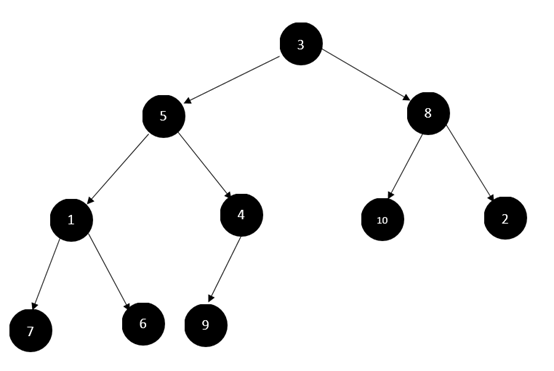
从我们要对从最后一个非叶子节点开始向上到根节点中,所有的节点进行调整,也就是一次对4、1、8、5、3节点进行一次直到叶子节点的调整。
对4号节点,也就是4元素:
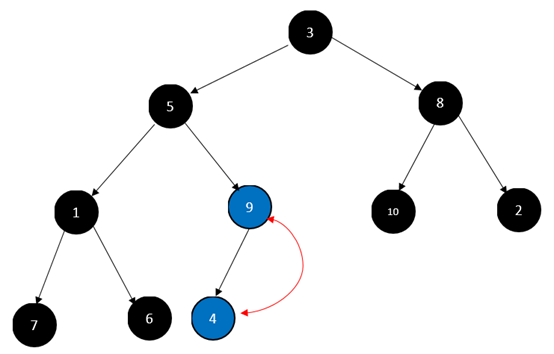
对3号节点,也就是1元素:
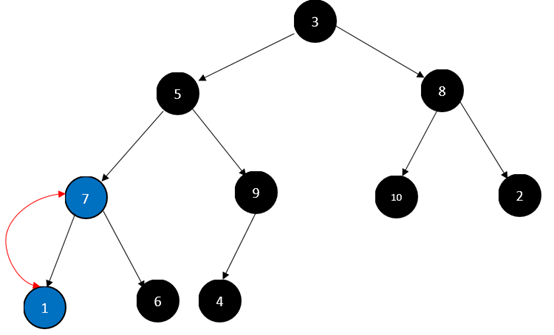
对2号节点,也就是8元素:

对1号节点,也就是5元素:
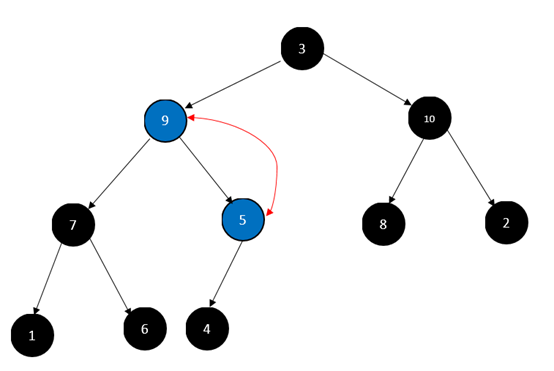
注意,此时新的起点5和它叶子之间整好满足大顶堆所以不需要继续调整,如果碰到不满足的要继续调整,直到叶子节点。
对于0号节点,也就是3元素:
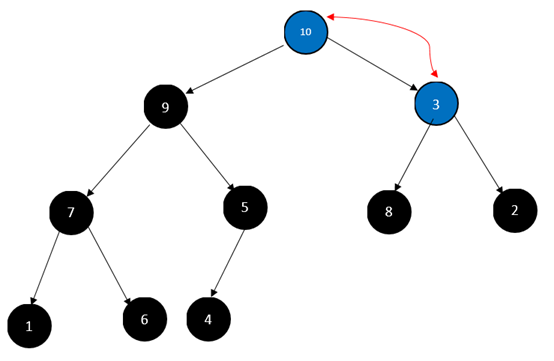
此时新的起点3,和它的叶子节点8、2并不满足大顶堆,所以要继续调整:

新的起点是叶子节点了,结束。
此时已经对从最后一个非叶子节点到根节点中所有的节点都调整了,此时,整棵树已经满足大顶堆了。
需要注意的就是,对每个节点的调整都要直到叶子节点为止(当然,如果这个过程中,已经满足条件了,就不需要直到叶子节点了)
源代码:
#include <stdio.h> /** * 求一个节点的父亲节点的下标 * 参数为该节点的下标 * */ int get_parent(int index) { return (index - 1) >> 1; //按位右移比除法效率高 } /** * 获取左子节点的下标 * 参数为该节点的下标 * */ int get_left(int index) { return (index << 1) + 1; //按位左移比乘法效率高 } /** * 获取右子节点的下标 * 参数为该节点的下标 * */ int get_right(int index) { return (index << 1) + 2; } /** * 求最后一个非叶子节点的下标 * 数组下标从0开始 * 参数len为数组的长度 * */ int get_ln_leaf_i(int len) { //下标从0开始的数组,长度为len,则最后一个节点的下标为len-1,最后一个非叶子节点就是最后一个节点的父亲节点 return get_parent(len - 1); } /** * 求数组中三个数的最大值的下标 * 参数为三个数的下标 * 返回值为最大值下标 * */ int get_max_index(int value[],int a,int b,int c) { int max_index; if(value[a] > value[b]) max_index = a; else max_index = b; if(value[max_index] < value[c]) max_index = c; return max_index; } /** * 从下标begin_index开始调整,使得以begin_index节点为根的树满足堆的要求 * 参数value表示待排序的数组,len是数组的长度,begin_index是开始调整的下标,ln_leaf_i是最后一个非叶子节点的下标 * */ static void adjust(int value[],int len,int begin_index,int ln_leaf_i) { do{ int left = get_left(begin_index); int right = get_right(begin_index); int max_index; //注意可能没有右孩子 if(right >= len)//说明起始没有右孩子 { if(value[begin_index] > value[left]) break; max_index = left; } else max_index = get_max_index(value,begin_index,left,right); if(max_index == begin_index)//如果本节点比两个孩子都大,说明已经满足堆的条件了,结束 break; //否则,交换该节点与最大值节点 //用异或的方式交换效率比较高 value[begin_index] ^= value[max_index]; value[max_index] ^= value[begin_index]; value[begin_index] ^= value[max_index]; //更新起始节点,继续 begin_index = max_index; }while(begin_index <= ln_leaf_i);//直到最后一个非叶子节点 } /** * 初始化堆 * */ void init_heap(int value[],int len) { /** * 初始化堆的过程就是: * 从最后一个非叶子节点开始,向树根, * 对这其中所有的节点,都进行依次adjust操作 * */ int ln_leaf_i = get_ln_leaf_i(len);//最后一个非叶子节点 int i = ln_leaf_i; for(;i >= 0;i--) { adjust(value,len,i,ln_leaf_i); } } void heap_sort(int value[],int len) { init_heap(value,len); printf("创建的堆为:\n"); int j = 0; for(;j < len;j++) { printf("%d ",value[j]); } printf("\n"); int i = len-1;//最后一个元素的下标 for(;i > 0;i--) { //交换最后一个节点和树根元素 //用异或的方式交换效率比较高 value[0] ^= value[i]; value[i] ^= value[0]; value[0] ^= value[i]; /**从根节点开始进行调整 * 注意由于数组的最后一个元素已经在正确的位置了 * 所以只对[0...i-1]这个数组进行调整就好 * */ if(i == 1)//当只有一个元素时,就不需要筛下啦 break; int ln_leaf_i = get_ln_leaf_i(i);//这里i就是剩下的数组的长度 adjust(value,i,0,ln_leaf_i); } } int main() { int value[] = {3,5,8,1,4,10,2,7,6,9}; int n = 10; heap_sort(value,n); printf("排序结果为:\n"); int i = 0; for(;i < n;i++) { printf("%d ",value[i]); } printf("\n"); return 0; }
10月11日更新,修改了堆排序函数,使用了递归,思路更加清晰,简洁
#include <stdio.h> /** * 获取左子节点的下标 * 参数为该节点的下标 * */ int get_left(int index) { return (index << 1) + 1; //按位左移比乘法效率高 } /** * 获取右子节点的下标 * 参数为该节点的下标 * */ int get_right(int index) { return (index << 1) + 2; } /** * 求数组中三个数的最大值的下标 * 参数为三个数的下标 * 返回值为最大值下标 * */ int get_max_index(int value[],int a,int b,int c) { int max_index; if(value[a] > value[b]) max_index = a; else max_index = b; if(value[max_index] < value[c]) max_index = c; return max_index; } //交换两个数 void swap(int *a,int *b) { *a^=*b; *b^=*a; *a^=*b; } /** * 从下标begin开始调整,使得以begin节点为根的树满足堆的要求 * 参数value表示待排序的数组,len是数组的长度,begin是开始调整的下标 * * 递归调用,递归出口为:没有左右孩子时,或者有孩子但是不需要调整时 * */ static void adjust(int value[],int len,int begin) { int left = get_left(begin);//左孩子下标 int right = get_right(begin);//右孩子下标 int max = begin;//记录最大值的下标 if(right < len)//说明左右孩子都存在 { max = get_max_index(value,begin,left,right);//获得最大值下标 } else//说明不存在右孩子 { if(left < len)//说明存在左孩子 { if(value[begin] < value[left]) max = left; } //else的情况是左右节点都不存在的情况,这时也是递归出口 } if(max == begin)//说明不需要调整,也是一个递归出口 return; swap(&value[begin],&value[max]);//调整 adjust(value,len,max);//递归调用 } /** * 初始化堆 * */ void init_heap(int value[],int len) { //初始化堆,从最后一个非叶子节点开始调整,也就是调用adjust,直到根结点 int i = (len - 1) >> 1;//最后一个非叶子节点的下标 for(;i >= 0;i--) { adjust(value,len,i); } } void heap_sort(int value[],int len) { init_heap(value,len); printf("创建的堆为:\n"); int j = 0; for(;j < len;j++) { printf("%d ",value[j]); } printf("\n"); int i = len-1;//最后一个元素的下标 for(;i > 0;i--) { swap(&value[0],&value[i]);//顶元素筛下 adjust(value,i,0);//从根节点开始调整,注意无序的数组长度逐渐减小 } } int main() { int value[] = {3,5,8,1,4,10,2,7,6,9}; int n = 10; heap_sort(value,n); printf("排序结果为:\n"); int i = 0; for(;i < n;i++) { printf("%d ",value[i]); } printf("\n"); return 0; }
堆排序的时间复杂度
如果初始建立的堆已经是有序的,此时就不需要堆进行顶元素筛下和调整。最坏的情况,每次顶元素筛下后,都需要进行直到叶子节点的调整,那么此次调整实际上就形成从根到叶子的一条路径,路径长度为树的高度,对于满树,树高为:log2(n+1),对于完全二叉树是该中向上取正。所以最坏情况,每次调整都需要O(log2n),要进行n-1次顶元素的筛下,虽然每次调整n在逐渐减小,但应该可以证明,整个筛下排序过程需要O(nlog2n).
创建堆需要O(n),从书上看到了,不会证明。
所以最坏情况下堆排序的时间复杂度是O(nlog2n),这一点比那个牛掰的快排序都好。
参考文献
http://www.cnblogs.com/luchen927/archive/2012/02/27/2367108.html
http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html
最后附上word和源码的链接
链接:http://pan.baidu.com/s/1skMrit3 密码:dzu2
如果你觉得对你有用,请点赞吧~~




