STEAM密码逆向

需求

Steam站登录密码逆向破解，提供逆向破解成功模块steam.py，爬虫通过调用该模块中的方法获取登录密码进行后续操作。

url：https://store.steampowered.com/

具体流程

加密说明：

对称和非对称加密中都需要用到相关的秘钥。对称加密中只需要一个公钥即可。

非对称中加密和解密分别使用的公钥和私钥，这些公钥和秘钥不会以明文展示，可能是通过其它的方式生成之后去用，需要将秘钥的生成方式找到。

前段代码分析：

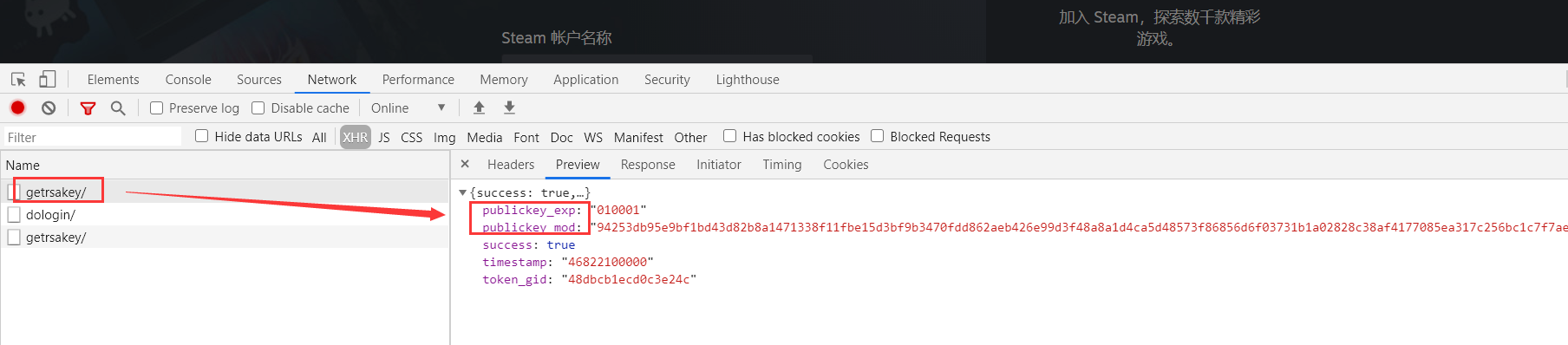
通过谷歌浏览器开发者工具调试登录请求，发现使用了RSA非对称加密方式。

登录时发送了两个请求：

请求1：https://store.steampowered.com/login/getrsakey/ 返回了json字符串，其中publickey_exp，publickey_mod两个字段的值为RSA.getPublicKey(mod, exp)函数加密时的参数。

请求2：https://store.steampowered.com/login/dologin/ 登录form表单

 

 

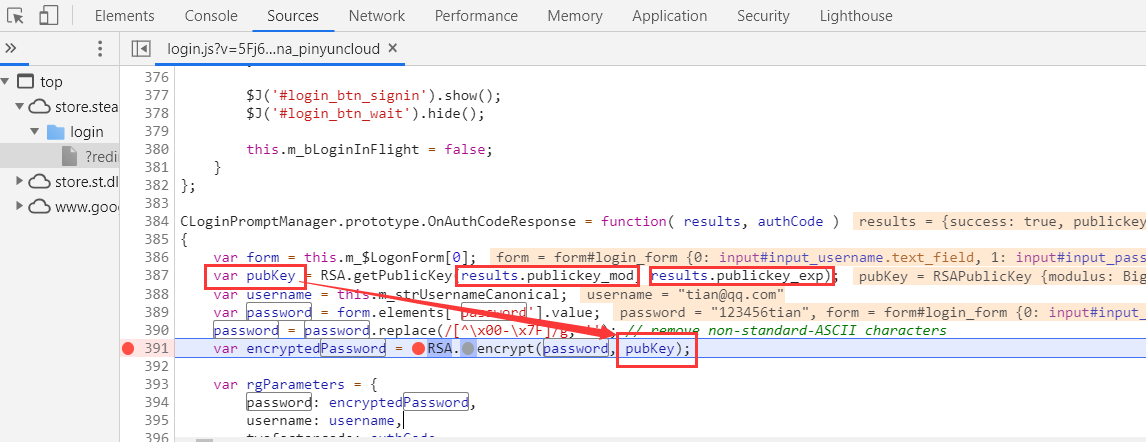
调试成功的steam.js

navigator = this;
// Copyright (c) 2005  Tom Wu
// All Rights Reserved.
// See "LICENSE" for details.

/*
 * Copyright (c) 2003-2005  Tom Wu
 * All Rights Reserved.
 *
 * Permission is hereby granted, free of charge, to any person obtaining
 * a copy of this software and associated documentation files (the
 * "Software"), to deal in the Software without restriction, including
 * without limitation the rights to use, copy, modify, merge, publish,
 * distribute, sublicense, and/or sell copies of the Software, and to
 * permit persons to whom the Software is furnished to do so, subject to
 * the following conditions:
 *
 * The above copyright notice and this permission notice shall be
 * included in all copies or substantial portions of the Software.
 *
 * THE SOFTWARE IS PROVIDED "AS-IS" AND WITHOUT WARRANTY OF ANY KIND, 
 * EXPRESS, IMPLIED OR OTHERWISE, INCLUDING WITHOUT LIMITATION, ANY 
 * WARRANTY OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE.  
 *
 * IN NO EVENT SHALL TOM WU BE LIABLE FOR ANY SPECIAL, INCIDENTAL,
 * INDIRECT OR CONSEQUENTIAL DAMAGES OF ANY KIND, OR ANY DAMAGES WHATSOEVER
 * RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER OR NOT ADVISED OF
 * THE POSSIBILITY OF DAMAGE, AND ON ANY THEORY OF LIABILITY, ARISING OUT
 * OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 *
 * In addition, the following condition applies:
 *
 * All redistributions must retain an intact copy of this copyright notice
 * and disclaimer.
 */

// Basic JavaScript BN library - subset useful for RSA encryption.

// Bits per digit
var dbits;

// JavaScript engine analysis
var canary = 0xdeadbeefcafe;
var j_lm = ((canary & 0xffffff) == 0xefcafe);

// (public) Constructor
function BigInteger(a, b, c) {
if (a != null) if ("number" == typeof a) this.fromNumber(a, b, c);
else if (b == null && "string" != typeof a) this.fromString(a, 256);
else this.fromString(a, b);
}

// return new, unset BigInteger
function nbi() {
return new BigInteger(null);
}

// am: Compute w_j += (x*this_i), propagate carries,
// c is initial carry, returns final carry.
// c < 3*dvalue, x < 2*dvalue, this_i < dvalue
// We need to select the fastest one that works in this environment.

// am1: use a single mult and divide to get the high bits,
// max digit bits should be 26 because
// max internal value = 2*dvalue^2-2*dvalue (< 2^53)
function am1(i, x, w, j, c, n) {
while (--n >= 0) {
    var v = x * this[i++] + w[j] + c;
    c = Math.floor(v / 0x4000000);
    w[j++] = v & 0x3ffffff;
}
return c;
}
// am2 avoids a big mult-and-extract completely.
// Max digit bits should be <= 30 because we do bitwise ops
// on values up to 2*hdvalue^2-hdvalue-1 (< 2^31)
function am2(i, x, w, j, c, n) {
var xl = x & 0x7fff,
xh = x >> 15;
while (--n >= 0) {
    var l = this[i] & 0x7fff;
    var h = this[i++] >> 15;
    var m = xh * l + h * xl;
    l = xl * l + ((m & 0x7fff) << 15) + w[j] + (c & 0x3fffffff);
    c = (l >>> 30) + (m >>> 15) + xh * h + (c >>> 30);
    w[j++] = l & 0x3fffffff;
}
return c;
}
// Alternately, set max digit bits to 28 since some
// browsers slow down when dealing with 32-bit numbers.
function am3(i, x, w, j, c, n) {
var xl = x & 0x3fff,
xh = x >> 14;
while (--n >= 0) {
    var l = this[i] & 0x3fff;
    var h = this[i++] >> 14;
    var m = xh * l + h * xl;
    l = xl * l + ((m & 0x3fff) << 14) + w[j] + c;
    c = (l >> 28) + (m >> 14) + xh * h;
    w[j++] = l & 0xfffffff;
}
return c;
}
if (j_lm && (navigator.appName == "Microsoft Internet Explorer")) {
BigInteger.prototype.am = am2;
dbits = 30;
} else if (j_lm && (navigator.appName != "Netscape")) {
BigInteger.prototype.am = am1;
dbits = 26;
} else { // Mozilla/Netscape seems to prefer am3
BigInteger.prototype.am = am3;
dbits = 28;
}

BigInteger.prototype.DB = dbits;
BigInteger.prototype.DM = ((1 << dbits) - 1);
BigInteger.prototype.DV = (1 << dbits);

var BI_FP = 52;
BigInteger.prototype.FV = Math.pow(2, BI_FP);
BigInteger.prototype.F1 = BI_FP - dbits;
BigInteger.prototype.F2 = 2 * dbits - BI_FP;

// Digit conversions
var BI_RM = "0123456789abcdefghijklmnopqrstuvwxyz";
var BI_RC = new Array();
var rr, vv;
rr = "0".charCodeAt(0);
for (vv = 0; vv <= 9; ++vv) BI_RC[rr++] = vv;
rr = "a".charCodeAt(0);
for (vv = 10; vv < 36; ++vv) BI_RC[rr++] = vv;
rr = "A".charCodeAt(0);
for (vv = 10; vv < 36; ++vv) BI_RC[rr++] = vv;

function int2char(n) {
return BI_RM.charAt(n);
}
function intAt(s, i) {
var c = BI_RC[s.charCodeAt(i)];
return (c == null) ? -1 : c;
}

// (protected) copy this to r
function bnpCopyTo(r) {
for (var i = this.t - 1; i >= 0; --i) r[i] = this[i];
r.t = this.t;
r.s = this.s;
}

// (protected) set from integer value x, -DV <= x < DV
function bnpFromInt(x) {
this.t = 1;
this.s = (x < 0) ? -1 : 0;
if (x > 0) this[0] = x;
else if (x < -1) this[0] = x + DV;
else this.t = 0;
}

// return bigint initialized to value
function nbv(i) {
var r = nbi();
r.fromInt(i);
return r;
}

// (protected) set from string and radix
function bnpFromString(s, b) {
var k;
if (b == 16) k = 4;
else if (b == 8) k = 3;
else if (b == 256) k = 8; // byte array
else if (b == 2) k = 1;
else if (b == 32) k = 5;
else if (b == 4) k = 2;
else {
    this.fromRadix(s, b);
    return;
}
this.t = 0;
this.s = 0;
var i = s.length,
mi = false,
sh = 0;
while (--i >= 0) {
    var x = (k == 8) ? s[i] & 0xff: intAt(s, i);
    if (x < 0) {
        if (s.charAt(i) == "-") mi = true;
        continue;
    }
    mi = false;
    if (sh == 0) this[this.t++] = x;
    else if (sh + k > this.DB) {
        this[this.t - 1] |= (x & ((1 << (this.DB - sh)) - 1)) << sh;
        this[this.t++] = (x >> (this.DB - sh));
    } else this[this.t - 1] |= x << sh;
    sh += k;
    if (sh >= this.DB) sh -= this.DB;
}
if (k == 8 && (s[0] & 0x80) != 0) {
    this.s = -1;
    if (sh > 0) this[this.t - 1] |= ((1 << (this.DB - sh)) - 1) << sh;
}
this.clamp();
if (mi) BigInteger.ZERO.subTo(this, this);
}

// (protected) clamp off excess high words
function bnpClamp() {
var c = this.s & this.DM;
while (this.t > 0 && this[this.t - 1] == c)--this.t;
}

// (public) return string representation in given radix
function bnToString(b) {
if (this.s < 0) return "-" + this.negate().toString(b);
var k;
if (b == 16) k = 4;
else if (b == 8) k = 3;
else if (b == 2) k = 1;
else if (b == 32) k = 5;
else if (b == 4) k = 2;
else return this.toRadix(b);
var km = (1 << k) - 1,
d,
m = false,
r = "",
i = this.t;
var p = this.DB - (i * this.DB) % k;
if (i-->0) {
    if (p < this.DB && (d = this[i] >> p) > 0) {
        m = true;
        r = int2char(d);
    }
    while (i >= 0) {
        if (p < k) {
            d = (this[i] & ((1 << p) - 1)) << (k - p);
            d |= this[--i] >> (p += this.DB - k);
        } else {
            d = (this[i] >> (p -= k)) & km;
            if (p <= 0) {
                p += this.DB; --i;
            }
        }
        if (d > 0) m = true;
        if (m) r += int2char(d);
    }
}
return m ? r: "0";
}

// (public) -this
function bnNegate() {
var r = nbi();
BigInteger.ZERO.subTo(this, r);
return r;
}

// (public) |this|
function bnAbs() {
return (this.s < 0) ? this.negate() : this;
}

// (public) return + if this > a, - if this < a, 0 if equal
function bnCompareTo(a) {
var r = this.s - a.s;
if (r != 0) return r;
var i = this.t;
r = i - a.t;
if (r != 0) return r;
while (--i >= 0) if ((r = this[i] - a[i]) != 0) return r;
return 0;
}

// returns bit length of the integer x
function nbits(x) {
var r = 1,
t;
if ((t = x >>> 16) != 0) {
    x = t;
    r += 16;
}
if ((t = x >> 8) != 0) {
    x = t;
    r += 8;
}
if ((t = x >> 4) != 0) {
    x = t;
    r += 4;
}
if ((t = x >> 2) != 0) {
    x = t;
    r += 2;
}
if ((t = x >> 1) != 0) {
    x = t;
    r += 1;
}
return r;
}

// (public) return the number of bits in "this"
function bnBitLength() {
if (this.t <= 0) return 0;
return this.DB * (this.t - 1) + nbits(this[this.t - 1] ^ (this.s & this.DM));
}

// (protected) r = this << n*DB
function bnpDLShiftTo(n, r) {
var i;
for (i = this.t - 1; i >= 0; --i) r[i + n] = this[i];
for (i = n - 1; i >= 0; --i) r[i] = 0;
r.t = this.t + n;
r.s = this.s;
}

// (protected) r = this >> n*DB
function bnpDRShiftTo(n, r) {
for (var i = n; i < this.t; ++i) r[i - n] = this[i];
r.t = Math.max(this.t - n, 0);
r.s = this.s;
}

// (protected) r = this << n
function bnpLShiftTo(n, r) {
var bs = n % this.DB;
var cbs = this.DB - bs;
var bm = (1 << cbs) - 1;
var ds = Math.floor(n / this.DB),
c = (this.s << bs) & this.DM,
i;
for (i = this.t - 1; i >= 0; --i) {
    r[i + ds + 1] = (this[i] >> cbs) | c;
    c = (this[i] & bm) << bs;
}
for (i = ds - 1; i >= 0; --i) r[i] = 0;
r[ds] = c;
r.t = this.t + ds + 1;
r.s = this.s;
r.clamp();
}

// (protected) r = this >> n
function bnpRShiftTo(n, r) {
r.s = this.s;
var ds = Math.floor(n / this.DB);
if (ds >= this.t) {
    r.t = 0;
    return;
}
var bs = n % this.DB;
var cbs = this.DB - bs;
var bm = (1 << bs) - 1;
r[0] = this[ds] >> bs;
for (var i = ds + 1; i < this.t; ++i) {
    r[i - ds - 1] |= (this[i] & bm) << cbs;
    r[i - ds] = this[i] >> bs;
}
if (bs > 0) r[this.t - ds - 1] |= (this.s & bm) << cbs;
r.t = this.t - ds;
r.clamp();
}

// (protected) r = this - a
function bnpSubTo(a, r) {
var i = 0,
c = 0,
m = Math.min(a.t, this.t);
while (i < m) {
    c += this[i] - a[i];
    r[i++] = c & this.DM;
    c >>= this.DB;
}
if (a.t < this.t) {
    c -= a.s;
    while (i < this.t) {
        c += this[i];
        r[i++] = c & this.DM;
        c >>= this.DB;
    }
    c += this.s;
} else {
    c += this.s;
    while (i < a.t) {
        c -= a[i];
        r[i++] = c & this.DM;
        c >>= this.DB;
    }
    c -= a.s;
}
r.s = (c < 0) ? -1 : 0;
if (c < -1) r[i++] = this.DV + c;
else if (c > 0) r[i++] = c;
r.t = i;
r.clamp();
}

// (protected) r = this * a, r != this,a (HAC 14.12)
// "this" should be the larger one if appropriate.
function bnpMultiplyTo(a, r) {
var x = this.abs(),
y = a.abs();
var i = x.t;
r.t = i + y.t;
while (--i >= 0) r[i] = 0;
for (i = 0; i < y.t; ++i) r[i + x.t] = x.am(0, y[i], r, i, 0, x.t);
r.s = 0;
r.clamp();
if (this.s != a.s) BigInteger.ZERO.subTo(r, r);
}

// (protected) r = this^2, r != this (HAC 14.16)
function bnpSquareTo(r) {
var x = this.abs();
var i = r.t = 2 * x.t;
while (--i >= 0) r[i] = 0;
for (i = 0; i < x.t - 1; ++i) {
    var c = x.am(i, x[i], r, 2 * i, 0, 1);
    if ((r[i + x.t] += x.am(i + 1, 2 * x[i], r, 2 * i + 1, c, x.t - i - 1)) >= x.DV) {
        r[i + x.t] -= x.DV;
        r[i + x.t + 1] = 1;
    }
}
if (r.t > 0) r[r.t - 1] += x.am(i, x[i], r, 2 * i, 0, 1);
r.s = 0;
r.clamp();
}

// (protected) divide this by m, quotient and remainder to q, r (HAC 14.20)
// r != q, this != m.  q or r may be null.
function bnpDivRemTo(m, q, r) {
var pm = m.abs();
if (pm.t <= 0) return;
var pt = this.abs();
if (pt.t < pm.t) {
    if (q != null) q.fromInt(0);
    if (r != null) this.copyTo(r);
    return;
}
if (r == null) r = nbi();
var y = nbi(),
ts = this.s,
ms = m.s;
var nsh = this.DB - nbits(pm[pm.t - 1]); // normalize modulus
if (nsh > 0) {
    pm.lShiftTo(nsh, y);
    pt.lShiftTo(nsh, r);
} else {
    pm.copyTo(y);
    pt.copyTo(r);
}
var ys = y.t;
var y0 = y[ys - 1];
if (y0 == 0) return;
var yt = y0 * (1 << this.F1) + ((ys > 1) ? y[ys - 2] >> this.F2: 0);
var d1 = this.FV / yt,
d2 = (1 << this.F1) / yt,
e = 1 << this.F2;
var i = r.t,
j = i - ys,
t = (q == null) ? nbi() : q;
y.dlShiftTo(j, t);
if (r.compareTo(t) >= 0) {
    r[r.t++] = 1;
    r.subTo(t, r);
}
BigInteger.ONE.dlShiftTo(ys, t);
t.subTo(y, y); // "negative" y so we can replace sub with am later
while (y.t < ys) y[y.t++] = 0;
while (--j >= 0) {
    // Estimate quotient digit
    var qd = (r[--i] == y0) ? this.DM: Math.floor(r[i] * d1 + (r[i - 1] + e) * d2);
    if ((r[i] += y.am(0, qd, r, j, 0, ys)) < qd) { // Try it out
        y.dlShiftTo(j, t);
        r.subTo(t, r);
        while (r[i] < --qd) r.subTo(t, r);
    }
}
if (q != null) {
    r.drShiftTo(ys, q);
    if (ts != ms) BigInteger.ZERO.subTo(q, q);
}
r.t = ys;
r.clamp();
if (nsh > 0) r.rShiftTo(nsh, r); // Denormalize remainder
if (ts < 0) BigInteger.ZERO.subTo(r, r);
}

// (public) this mod a
function bnMod(a) {
var r = nbi();
this.abs().divRemTo(a, null, r);
if (this.s < 0 && r.compareTo(BigInteger.ZERO) > 0) a.subTo(r, r);
return r;
}

// Modular reduction using "classic" algorithm
function Classic(m) {
this.m = m;
}
function cConvert(x) {
if (x.s < 0 || x.compareTo(this.m) >= 0) return x.mod(this.m);
else return x;
}
function cRevert(x) {
return x;
}
function cReduce(x) {
x.divRemTo(this.m, null, x);
}
function cMulTo(x, y, r) {
x.multiplyTo(y, r);
this.reduce(r);
}
function cSqrTo(x, r) {
x.squareTo(r);
this.reduce(r);
}

Classic.prototype.convert = cConvert;
Classic.prototype.revert = cRevert;
Classic.prototype.reduce = cReduce;
Classic.prototype.mulTo = cMulTo;
Classic.prototype.sqrTo = cSqrTo;

// (protected) return "-1/this % 2^DB"; useful for Mont. reduction
// justification:
//         xy == 1 (mod m)
//         xy =  1+km
//   xy(2-xy) = (1+km)(1-km)
// x[y(2-xy)] = 1-k^2m^2
// x[y(2-xy)] == 1 (mod m^2)
// if y is 1/x mod m, then y(2-xy) is 1/x mod m^2
// should reduce x and y(2-xy) by m^2 at each step to keep size bounded.
// JS multiply "overflows" differently from C/C++, so care is needed here.
function bnpInvDigit() {
if (this.t < 1) return 0;
var x = this[0];
if ((x & 1) == 0) return 0;
var y = x & 3; // y == 1/x mod 2^2
y = (y * (2 - (x & 0xf) * y)) & 0xf; // y == 1/x mod 2^4
y = (y * (2 - (x & 0xff) * y)) & 0xff; // y == 1/x mod 2^8
y = (y * (2 - (((x & 0xffff) * y) & 0xffff))) & 0xffff; // y == 1/x mod 2^16
// last step - calculate inverse mod DV directly;
// assumes 16 < DB <= 32 and assumes ability to handle 48-bit ints
y = (y * (2 - x * y % this.DV)) % this.DV; // y == 1/x mod 2^dbits
// we really want the negative inverse, and -DV < y < DV
return (y > 0) ? this.DV - y: -y;
}

// Montgomery reduction
function Montgomery(m) {
this.m = m;
this.mp = m.invDigit();
this.mpl = this.mp & 0x7fff;
this.mph = this.mp >> 15;
this.um = (1 << (m.DB - 15)) - 1;
this.mt2 = 2 * m.t;
}

// xR mod m
function montConvert(x) {
var r = nbi();
x.abs().dlShiftTo(this.m.t, r);
r.divRemTo(this.m, null, r);
if (x.s < 0 && r.compareTo(BigInteger.ZERO) > 0) this.m.subTo(r, r);
return r;
}

// x/R mod m
function montRevert(x) {
var r = nbi();
x.copyTo(r);
this.reduce(r);
return r;
}

// x = x/R mod m (HAC 14.32)
function montReduce(x) {
while (x.t <= this.mt2) // pad x so am has enough room later
x[x.t++] = 0;
for (var i = 0; i < this.m.t; ++i) {
    // faster way of calculating u0 = x[i]*mp mod DV
    var j = x[i] & 0x7fff;
    var u0 = (j * this.mpl + (((j * this.mph + (x[i] >> 15) * this.mpl) & this.um) << 15)) & x.DM;
    // use am to combine the multiply-shift-add into one call
    j = i + this.m.t;
    x[j] += this.m.am(0, u0, x, i, 0, this.m.t);
    // propagate carry
    while (x[j] >= x.DV) {
        x[j] -= x.DV;
        x[++j]++;
    }
}
x.clamp();
x.drShiftTo(this.m.t, x);
if (x.compareTo(this.m) >= 0) x.subTo(this.m, x);
}

// r = "x^2/R mod m"; x != r
function montSqrTo(x, r) {
x.squareTo(r);
this.reduce(r);
}

// r = "xy/R mod m"; x,y != r
function montMulTo(x, y, r) {
x.multiplyTo(y, r);
this.reduce(r);
}

Montgomery.prototype.convert = montConvert;
Montgomery.prototype.revert = montRevert;
Montgomery.prototype.reduce = montReduce;
Montgomery.prototype.mulTo = montMulTo;
Montgomery.prototype.sqrTo = montSqrTo;

// (protected) true iff this is even
function bnpIsEven() {
return ((this.t > 0) ? (this[0] & 1) : this.s) == 0;
}

// (protected) this^e, e < 2^32, doing sqr and mul with "r" (HAC 14.79)
function bnpExp(e, z) {
if (e > 0xffffffff || e < 1) return BigInteger.ONE;
var r = nbi(),
r2 = nbi(),
g = z.convert(this),
i = nbits(e) - 1;
g.copyTo(r);
while (--i >= 0) {
    z.sqrTo(r, r2);
    if ((e & (1 << i)) > 0) z.mulTo(r2, g, r);
    else {
        var t = r;
        r = r2;
        r2 = t;
    }
}
return z.revert(r);
}

// (public) this^e % m, 0 <= e < 2^32
function bnModPowInt(e, m) {
var z;
if (e < 256 || m.isEven()) z = new Classic(m);
else z = new Montgomery(m);
return this.exp(e, z);
}

// protected
BigInteger.prototype.copyTo = bnpCopyTo;
BigInteger.prototype.fromInt = bnpFromInt;
BigInteger.prototype.fromString = bnpFromString;
BigInteger.prototype.clamp = bnpClamp;
BigInteger.prototype.dlShiftTo = bnpDLShiftTo;
BigInteger.prototype.drShiftTo = bnpDRShiftTo;
BigInteger.prototype.lShiftTo = bnpLShiftTo;
BigInteger.prototype.rShiftTo = bnpRShiftTo;
BigInteger.prototype.subTo = bnpSubTo;
BigInteger.prototype.multiplyTo = bnpMultiplyTo;
BigInteger.prototype.squareTo = bnpSquareTo;
BigInteger.prototype.divRemTo = bnpDivRemTo;
BigInteger.prototype.invDigit = bnpInvDigit;
BigInteger.prototype.isEven = bnpIsEven;
BigInteger.prototype.exp = bnpExp;

// public
BigInteger.prototype.toString = bnToString;
BigInteger.prototype.negate = bnNegate;
BigInteger.prototype.abs = bnAbs;
BigInteger.prototype.compareTo = bnCompareTo;
BigInteger.prototype.bitLength = bnBitLength;
BigInteger.prototype.mod = bnMod;
BigInteger.prototype.modPowInt = bnModPowInt;

// "constants"
BigInteger.ZERO = nbv(0);
BigInteger.ONE = nbv(1);

// Copyright (c) 2005  Tom Wu
// All Rights Reserved.
// See "LICENSE" for details.

// Extended JavaScript BN functions, required for RSA private ops.

// (public)
function bnClone() {
var r = nbi();
this.copyTo(r);
return r;
}

// (public) return value as integer
function bnIntValue() {
if (this.s < 0) {
    if (this.t == 1) return this[0] - this.DV;
    else if (this.t == 0) return - 1;
} else if (this.t == 1) return this[0];
else if (this.t == 0) return 0;
// assumes 16 < DB < 32
return ((this[1] & ((1 << (32 - this.DB)) - 1)) << this.DB) | this[0];
}

// (public) return value as byte
function bnByteValue() {
return (this.t == 0) ? this.s: (this[0] << 24) >> 24;
}

// (public) return value as short (assumes DB>=16)
function bnShortValue() {
return (this.t == 0) ? this.s: (this[0] << 16) >> 16;
}

// (protected) return x s.t. r^x < DV
function bnpChunkSize(r) {
return Math.floor(Math.LN2 * this.DB / Math.log(r));
}

// (public) 0 if this == 0, 1 if this > 0
function bnSigNum() {
if (this.s < 0) return - 1;
else if (this.t <= 0 || (this.t == 1 && this[0] <= 0)) return 0;
else return 1;
}

// (protected) convert to radix string
function bnpToRadix(b) {
if (b == null) b = 10;
if (this.signum() == 0 || b < 2 || b > 36) return "0";
var cs = this.chunkSize(b);
var a = Math.pow(b, cs);
var d = nbv(a),
y = nbi(),
z = nbi(),
r = "";
this.divRemTo(d, y, z);
while (y.signum() > 0) {
    r = (a + z.intValue()).toString(b).substr(1) + r;
    y.divRemTo(d, y, z);
}
return z.intValue().toString(b) + r;
}

// (protected) convert from radix string
function bnpFromRadix(s, b) {
this.fromInt(0);
if (b == null) b = 10;
var cs = this.chunkSize(b);
var d = Math.pow(b, cs),
mi = false,
j = 0,
w = 0;
for (var i = 0; i < s.length; ++i) {
    var x = intAt(s, i);
    if (x < 0) {
        if (s.charAt(i) == "-" && this.signum() == 0) mi = true;
        continue;
    }
    w = b * w + x;
    if (++j >= cs) {
        this.dMultiply(d);
        this.dAddOffset(w, 0);
        j = 0;
        w = 0;
    }
}
if (j > 0) {
    this.dMultiply(Math.pow(b, j));
    this.dAddOffset(w, 0);
}
if (mi) BigInteger.ZERO.subTo(this, this);
}

// (protected) alternate constructor
function bnpFromNumber(a, b, c) {
if ("number" == typeof b) {
    // new BigInteger(int,int,RNG)
    if (a < 2) this.fromInt(1);
    else {
        this.fromNumber(a, c);
        if (!this.testBit(a - 1)) // force MSB set
        this.bitwiseTo(BigInteger.ONE.shiftLeft(a - 1), op_or, this);
        if (this.isEven()) this.dAddOffset(1, 0); // force odd
        while (!this.isProbablePrime(b)) {
            this.dAddOffset(2, 0);
            if (this.bitLength() > a) this.subTo(BigInteger.ONE.shiftLeft(a - 1), this);
        }
    }
} else {
    // new BigInteger(int,RNG)
    var x = new Array(),
    t = a & 7;
    x.length = (a >> 3) + 1;
    b.nextBytes(x);
    if (t > 0) x[0] &= ((1 << t) - 1);
    else x[0] = 0;
    this.fromString(x, 256);
}
}

// (public) convert to bigendian byte array
function bnToByteArray() {
var i = this.t,
r = new Array();
r[0] = this.s;
var p = this.DB - (i * this.DB) % 8,
d,
k = 0;
if (i-->0) {
    if (p < this.DB && (d = this[i] >> p) != (this.s & this.DM) >> p) r[k++] = d | (this.s << (this.DB - p));
    while (i >= 0) {
        if (p < 8) {
            d = (this[i] & ((1 << p) - 1)) << (8 - p);
            d |= this[--i] >> (p += this.DB - 8);
        } else {
            d = (this[i] >> (p -= 8)) & 0xff;
            if (p <= 0) {
                p += this.DB; --i;
            }
        }
        if ((d & 0x80) != 0) d |= -256;
        if (k == 0 && (this.s & 0x80) != (d & 0x80))++k;
        if (k > 0 || d != this.s) r[k++] = d;
    }
}
return r;
}

function bnEquals(a) {
return (this.compareTo(a) == 0);
}
function bnMin(a) {
return (this.compareTo(a) < 0) ? this: a;
}
function bnMax(a) {
return (this.compareTo(a) > 0) ? this: a;
}

// (protected) r = this op a (bitwise)
function bnpBitwiseTo(a, op, r) {
var i, f, m = Math.min(a.t, this.t);
for (i = 0; i < m; ++i) r[i] = op(this[i], a[i]);
if (a.t < this.t) {
    f = a.s & this.DM;
    for (i = m; i < this.t; ++i) r[i] = op(this[i], f);
    r.t = this.t;
} else {
    f = this.s & this.DM;
    for (i = m; i < a.t; ++i) r[i] = op(f, a[i]);
    r.t = a.t;
}
r.s = op(this.s, a.s);
r.clamp();
}

// (public) this & a
function op_and(x, y) {
return x & y;
}
function bnAnd(a) {
var r = nbi();
this.bitwiseTo(a, op_and, r);
return r;
}

// (public) this | a
function op_or(x, y) {
return x | y;
}
function bnOr(a) {
var r = nbi();
this.bitwiseTo(a, op_or, r);
return r;
}

// (public) this ^ a
function op_xor(x, y) {
return x ^ y;
}
function bnXor(a) {
var r = nbi();
this.bitwiseTo(a, op_xor, r);
return r;
}

// (public) this & ~a
function op_andnot(x, y) {
return x & ~y;
}
function bnAndNot(a) {
var r = nbi();
this.bitwiseTo(a, op_andnot, r);
return r;
}

// (public) ~this
function bnNot() {
var r = nbi();
for (var i = 0; i < this.t; ++i) r[i] = this.DM & ~this[i];
r.t = this.t;
r.s = ~this.s;
return r;
}

// (public) this << n
function bnShiftLeft(n) {
var r = nbi();
if (n < 0) this.rShiftTo( - n, r);
else this.lShiftTo(n, r);
return r;
}

// (public) this >> n
function bnShiftRight(n) {
var r = nbi();
if (n < 0) this.lShiftTo( - n, r);
else this.rShiftTo(n, r);
return r;
}

// return index of lowest 1-bit in x, x < 2^31
function lbit(x) {
if (x == 0) return - 1;
var r = 0;
if ((x & 0xffff) == 0) {
    x >>= 16;
    r += 16;
}
if ((x & 0xff) == 0) {
    x >>= 8;
    r += 8;
}
if ((x & 0xf) == 0) {
    x >>= 4;
    r += 4;
}
if ((x & 3) == 0) {
    x >>= 2;
    r += 2;
}
if ((x & 1) == 0)++r;
return r;
}

// (public) returns index of lowest 1-bit (or -1 if none)
function bnGetLowestSetBit() {
for (var i = 0; i < this.t; ++i) if (this[i] != 0) return i * this.DB + lbit(this[i]);
if (this.s < 0) return this.t * this.DB;
return - 1;
}

// return number of 1 bits in x
function cbit(x) {
var r = 0;
while (x != 0) {
    x &= x - 1; ++r;
}
return r;
}

// (public) return number of set bits
function bnBitCount() {
var r = 0,
x = this.s & this.DM;
for (var i = 0; i < this.t; ++i) r += cbit(this[i] ^ x);
return r;
}

// (public) true iff nth bit is set
function bnTestBit(n) {
var j = Math.floor(n / this.DB);
if (j >= this.t) return (this.s != 0);
return ((this[j] & (1 << (n % this.DB))) != 0);
}

// (protected) this op (1<<n)
function bnpChangeBit(n, op) {
var r = BigInteger.ONE.shiftLeft(n);
this.bitwiseTo(r, op, r);
return r;
}

// (public) this | (1<<n)
function bnSetBit(n) {
return this.changeBit(n, op_or);
}

// (public) this & ~(1<<n)
function bnClearBit(n) {
return this.changeBit(n, op_andnot);
}

// (public) this ^ (1<<n)
function bnFlipBit(n) {
return this.changeBit(n, op_xor);
}

// (protected) r = this + a
function bnpAddTo(a, r) {
var i = 0,
c = 0,
m = Math.min(a.t, this.t);
while (i < m) {
    c += this[i] + a[i];
    r[i++] = c & this.DM;
    c >>= this.DB;
}
if (a.t < this.t) {
    c += a.s;
    while (i < this.t) {
        c += this[i];
        r[i++] = c & this.DM;
        c >>= this.DB;
    }
    c += this.s;
} else {
    c += this.s;
    while (i < a.t) {
        c += a[i];
        r[i++] = c & this.DM;
        c >>= this.DB;
    }
    c += a.s;
}
r.s = (c < 0) ? -1 : 0;
if (c > 0) r[i++] = c;
else if (c < -1) r[i++] = this.DV + c;
r.t = i;
r.clamp();
}

// (public) this + a
function bnAdd(a) {
var r = nbi();
this.addTo(a, r);
return r;
}

// (public) this - a
function bnSubtract(a) {
var r = nbi();
this.subTo(a, r);
return r;
}

// (public) this * a
function bnMultiply(a) {
var r = nbi();
this.multiplyTo(a, r);
return r;
}

// (public) this / a
function bnDivide(a) {
var r = nbi();
this.divRemTo(a, r, null);
return r;
}

// (public) this % a
function bnRemainder(a) {
var r = nbi();
this.divRemTo(a, null, r);
return r;
}

// (public) [this/a,this%a]
function bnDivideAndRemainder(a) {
var q = nbi(),
r = nbi();
this.divRemTo(a, q, r);
return new Array(q, r);
}

// (protected) this *= n, this >= 0, 1 < n < DV
function bnpDMultiply(n) {
this[this.t] = this.am(0, n - 1, this, 0, 0, this.t); ++this.t;
this.clamp();
}

// (protected) this += n << w words, this >= 0
function bnpDAddOffset(n, w) {
while (this.t <= w) this[this.t++] = 0;
this[w] += n;
while (this[w] >= this.DV) {
    this[w] -= this.DV;
    if (++w >= this.t) this[this.t++] = 0; ++this[w];
}
}

// A "null" reducer
function NullExp() {}
function nNop(x) {
return x;
}
function nMulTo(x, y, r) {
x.multiplyTo(y, r);
}
function nSqrTo(x, r) {
x.squareTo(r);
}

NullExp.prototype.convert = nNop;
NullExp.prototype.revert = nNop;
NullExp.prototype.mulTo = nMulTo;
NullExp.prototype.sqrTo = nSqrTo;

// (public) this^e
function bnPow(e) {
return this.exp(e, new NullExp());
}

// (protected) r = lower n words of "this * a", a.t <= n
// "this" should be the larger one if appropriate.
function bnpMultiplyLowerTo(a, n, r) {
var i = Math.min(this.t + a.t, n);
r.s = 0; // assumes a,this >= 0
r.t = i;
while (i > 0) r[--i] = 0;
var j;
for (j = r.t - this.t; i < j; ++i) r[i + this.t] = this.am(0, a[i], r, i, 0, this.t);
for (j = Math.min(a.t, n); i < j; ++i) this.am(0, a[i], r, i, 0, n - i);
r.clamp();
}

// (protected) r = "this * a" without lower n words, n > 0
// "this" should be the larger one if appropriate.
function bnpMultiplyUpperTo(a, n, r) {--n;
var i = r.t = this.t + a.t - n;
r.s = 0; // assumes a,this >= 0
while (--i >= 0) r[i] = 0;
for (i = Math.max(n - this.t, 0); i < a.t; ++i) r[this.t + i - n] = this.am(n - i, a[i], r, 0, 0, this.t + i - n);
r.clamp();
r.drShiftTo(1, r);
}

// Barrett modular reduction
function Barrett(m) {
// setup Barrett
this.r2 = nbi();
this.q3 = nbi();
BigInteger.ONE.dlShiftTo(2 * m.t, this.r2);
this.mu = this.r2.divide(m);
this.m = m;
}

function barrettConvert(x) {
if (x.s < 0 || x.t > 2 * this.m.t) return x.mod(this.m);
else if (x.compareTo(this.m) < 0) return x;
else {
    var r = nbi();
    x.copyTo(r);
    this.reduce(r);
    return r;
}
}

function barrettRevert(x) {
return x;
}

// x = x mod m (HAC 14.42)
function barrettReduce(x) {
x.drShiftTo(this.m.t - 1, this.r2);
if (x.t > this.m.t + 1) {
    x.t = this.m.t + 1;
    x.clamp();
}
this.mu.multiplyUpperTo(this.r2, this.m.t + 1, this.q3);
this.m.multiplyLowerTo(this.q3, this.m.t + 1, this.r2);
while (x.compareTo(this.r2) < 0) x.dAddOffset(1, this.m.t + 1);
x.subTo(this.r2, x);
while (x.compareTo(this.m) >= 0) x.subTo(this.m, x);
}

// r = x^2 mod m; x != r
function barrettSqrTo(x, r) {
x.squareTo(r);
this.reduce(r);
}

// r = x*y mod m; x,y != r
function barrettMulTo(x, y, r) {
x.multiplyTo(y, r);
this.reduce(r);
}

Barrett.prototype.convert = barrettConvert;
Barrett.prototype.revert = barrettRevert;
Barrett.prototype.reduce = barrettReduce;
Barrett.prototype.mulTo = barrettMulTo;
Barrett.prototype.sqrTo = barrettSqrTo;

// (public) this^e % m (HAC 14.85)
function bnModPow(e, m) {
var i = e.bitLength(),
k,
r = nbv(1),
z;
if (i <= 0) return r;
else if (i < 18) k = 1;
else if (i < 48) k = 3;
else if (i < 144) k = 4;
else if (i < 768) k = 5;
else k = 6;
if (i < 8) z = new Classic(m);
else if (m.isEven()) z = new Barrett(m);
else z = new Montgomery(m);

// precomputation
var g = new Array(),
n = 3,
k1 = k - 1,
km = (1 << k) - 1;
g[1] = z.convert(this);
if (k > 1) {
    var g2 = nbi();
    z.sqrTo(g[1], g2);
    while (n <= km) {
        g[n] = nbi();
        z.mulTo(g2, g[n - 2], g[n]);
        n += 2;
    }
}

var j = e.t - 1,
w, is1 = true,
r2 = nbi(),
t;
i = nbits(e[j]) - 1;
while (j >= 0) {
    if (i >= k1) w = (e[j] >> (i - k1)) & km;
    else {
        w = (e[j] & ((1 << (i + 1)) - 1)) << (k1 - i);
        if (j > 0) w |= e[j - 1] >> (this.DB + i - k1);
    }

    n = k;
    while ((w & 1) == 0) {
        w >>= 1; --n;
    }
    if ((i -= n) < 0) {
        i += this.DB; --j;
    }
    if (is1) { // ret == 1, don't bother squaring or multiplying it
        g[w].copyTo(r);
        is1 = false;
    } else {
        while (n > 1) {
            z.sqrTo(r, r2);
            z.sqrTo(r2, r);
            n -= 2;
        }
        if (n > 0) z.sqrTo(r, r2);
        else {
            t = r;
            r = r2;
            r2 = t;
        }
        z.mulTo(r2, g[w], r);
    }

    while (j >= 0 && (e[j] & (1 << i)) == 0) {
        z.sqrTo(r, r2);
        t = r;
        r = r2;
        r2 = t;
        if (--i < 0) {
            i = this.DB - 1; --j;
        }
    }
}
return z.revert(r);
}

// (public) gcd(this,a) (HAC 14.54)
function bnGCD(a) {
var x = (this.s < 0) ? this.negate() : this.clone();
var y = (a.s < 0) ? a.negate() : a.clone();
if (x.compareTo(y) < 0) {
    var t = x;
    x = y;
    y = t;
}
var i = x.getLowestSetBit(),
g = y.getLowestSetBit();
if (g < 0) return x;
if (i < g) g = i;
if (g > 0) {
    x.rShiftTo(g, x);
    y.rShiftTo(g, y);
}
while (x.signum() > 0) {
    if ((i = x.getLowestSetBit()) > 0) x.rShiftTo(i, x);
    if ((i = y.getLowestSetBit()) > 0) y.rShiftTo(i, y);
    if (x.compareTo(y) >= 0) {
        x.subTo(y, x);
        x.rShiftTo(1, x);
    } else {
        y.subTo(x, y);
        y.rShiftTo(1, y);
    }
}
if (g > 0) y.lShiftTo(g, y);
return y;
}

// (protected) this % n, n < 2^26
function bnpModInt(n) {
if (n <= 0) return 0;
var d = this.DV % n,
r = (this.s < 0) ? n - 1 : 0;
if (this.t > 0) if (d == 0) r = this[0] % n;
else for (var i = this.t - 1; i >= 0; --i) r = (d * r + this[i]) % n;
return r;
}

// (public) 1/this % m (HAC 14.61)
function bnModInverse(m) {
var ac = m.isEven();
if ((this.isEven() && ac) || m.signum() == 0) return BigInteger.ZERO;
var u = m.clone(),
v = this.clone();
var a = nbv(1),
b = nbv(0),
c = nbv(0),
d = nbv(1);
while (u.signum() != 0) {
    while (u.isEven()) {
        u.rShiftTo(1, u);
        if (ac) {
            if (!a.isEven() || !b.isEven()) {
                a.addTo(this, a);
                b.subTo(m, b);
            }
            a.rShiftTo(1, a);
        } else if (!b.isEven()) b.subTo(m, b);
        b.rShiftTo(1, b);
    }
    while (v.isEven()) {
        v.rShiftTo(1, v);
        if (ac) {
            if (!c.isEven() || !d.isEven()) {
                c.addTo(this, c);
                d.subTo(m, d);
            }
            c.rShiftTo(1, c);
        } else if (!d.isEven()) d.subTo(m, d);
        d.rShiftTo(1, d);
    }
    if (u.compareTo(v) >= 0) {
        u.subTo(v, u);
        if (ac) a.subTo(c, a);
        b.subTo(d, b);
    } else {
        v.subTo(u, v);
        if (ac) c.subTo(a, c);
        d.subTo(b, d);
    }
}
if (v.compareTo(BigInteger.ONE) != 0) return BigInteger.ZERO;
if (d.compareTo(m) >= 0) return d.subtract(m);
if (d.signum() < 0) d.addTo(m, d);
else return d;
if (d.signum() < 0) return d.add(m);
else return d;
}

var lowprimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509];
var lplim = (1 << 26) / lowprimes[lowprimes.length - 1];

// (public) test primality with certainty >= 1-.5^t
function bnIsProbablePrime(t) {
var i, x = this.abs();
if (x.t == 1 && x[0] <= lowprimes[lowprimes.length - 1]) {
    for (i = 0; i < lowprimes.length; ++i) if (x[0] == lowprimes[i]) return true;
    return false;
}
if (x.isEven()) return false;
i = 1;
while (i < lowprimes.length) {
    var m = lowprimes[i],
    j = i + 1;
    while (j < lowprimes.length && m < lplim) m *= lowprimes[j++];
    m = x.modInt(m);
    while (i < j) if (m % lowprimes[i++] == 0) return false;
}
return x.millerRabin(t);
}

// (protected) true if probably prime (HAC 4.24, Miller-Rabin)
function bnpMillerRabin(t) {
var n1 = this.subtract(BigInteger.ONE);
var k = n1.getLowestSetBit();
if (k <= 0) return false;
var r = n1.shiftRight(k);
t = (t + 1) >> 1;
if (t > lowprimes.length) t = lowprimes.length;
var a = nbi();
for (var i = 0; i < t; ++i) {
    a.fromInt(lowprimes[i]);
    var y = a.modPow(r, this);
    if (y.compareTo(BigInteger.ONE) != 0 && y.compareTo(n1) != 0) {
        var j = 1;
        while (j++<k && y.compareTo(n1) != 0) {
            y = y.modPowInt(2, this);
            if (y.compareTo(BigInteger.ONE) == 0) return false;
        }
        if (y.compareTo(n1) != 0) return false;
    }
}
return true;
}

// protected
BigInteger.prototype.chunkSize = bnpChunkSize;
BigInteger.prototype.toRadix = bnpToRadix;
BigInteger.prototype.fromRadix = bnpFromRadix;
BigInteger.prototype.fromNumber = bnpFromNumber;
BigInteger.prototype.bitwiseTo = bnpBitwiseTo;
BigInteger.prototype.changeBit = bnpChangeBit;
BigInteger.prototype.addTo = bnpAddTo;
BigInteger.prototype.dMultiply = bnpDMultiply;
BigInteger.prototype.dAddOffset = bnpDAddOffset;
BigInteger.prototype.multiplyLowerTo = bnpMultiplyLowerTo;
BigInteger.prototype.multiplyUpperTo = bnpMultiplyUpperTo;
BigInteger.prototype.modInt = bnpModInt;
BigInteger.prototype.millerRabin = bnpMillerRabin;

// public
BigInteger.prototype.clone = bnClone;
BigInteger.prototype.intValue = bnIntValue;
BigInteger.prototype.byteValue = bnByteValue;
BigInteger.prototype.shortValue = bnShortValue;
BigInteger.prototype.signum = bnSigNum;
BigInteger.prototype.toByteArray = bnToByteArray;
BigInteger.prototype.equals = bnEquals;
BigInteger.prototype.min = bnMin;
BigInteger.prototype.max = bnMax;
BigInteger.prototype.and = bnAnd;
BigInteger.prototype.or = bnOr;
BigInteger.prototype.xor = bnXor;
BigInteger.prototype.andNot = bnAndNot;
BigInteger.prototype.not = bnNot;
BigInteger.prototype.shiftLeft = bnShiftLeft;
BigInteger.prototype.shiftRight = bnShiftRight;
BigInteger.prototype.getLowestSetBit = bnGetLowestSetBit;
BigInteger.prototype.bitCount = bnBitCount;
BigInteger.prototype.testBit = bnTestBit;
BigInteger.prototype.setBit = bnSetBit;
BigInteger.prototype.clearBit = bnClearBit;
BigInteger.prototype.flipBit = bnFlipBit;
BigInteger.prototype.add = bnAdd;
BigInteger.prototype.subtract = bnSubtract;
BigInteger.prototype.multiply = bnMultiply;
BigInteger.prototype.divide = bnDivide;
BigInteger.prototype.remainder = bnRemainder;
BigInteger.prototype.divideAndRemainder = bnDivideAndRemainder;
BigInteger.prototype.modPow = bnModPow;
BigInteger.prototype.modInverse = bnModInverse;
BigInteger.prototype.pow = bnPow;
BigInteger.prototype.gcd = bnGCD;
BigInteger.prototype.isProbablePrime = bnIsProbablePrime;

// BigInteger interfaces not implemented in jsbn:

// BigInteger(int signum, byte[] magnitude)
// double doubleValue()
// float floatValue()
// int hashCode()
// long longValue()
// static BigInteger valueOf(long val)

var RSAPublicKey = function($modulus_hex, $encryptionExponent_hex) {
this.modulus = new BigInteger($modulus_hex, 16);
this.encryptionExponent = new BigInteger($encryptionExponent_hex, 16);
};

var Base64 = {
base64: "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/=",
encode: function($input) {
    if (!$input) {
        return false;
    }
    var $output = "";
    var $chr1, $chr2, $chr3;
    var $enc1, $enc2, $enc3, $enc4;
    var $i = 0;
    do {
        $chr1 = $input.charCodeAt($i++);
        $chr2 = $input.charCodeAt($i++);
        $chr3 = $input.charCodeAt($i++);
        $enc1 = $chr1 >> 2;
        $enc2 = (($chr1 & 3) << 4) | ($chr2 >> 4);
        $enc3 = (($chr2 & 15) << 2) | ($chr3 >> 6);
        $enc4 = $chr3 & 63;
        if (isNaN($chr2)) $enc3 = $enc4 = 64;
        else if (isNaN($chr3)) $enc4 = 64;
        $output += this.base64.charAt($enc1) + this.base64.charAt($enc2) + this.base64.charAt($enc3) + this.base64.charAt($enc4);
    } while ( $i < $input . length );
    return $output;
},
decode: function($input) {
    if (!$input) return false;
    $input = $input.replace(/[^A-Za-z0-9\+\/\=]/g, "");
    var $output = "";
    var $enc1, $enc2, $enc3, $enc4;
    var $i = 0;
    do {
        $enc1 = this.base64.indexOf($input.charAt($i++));
        $enc2 = this.base64.indexOf($input.charAt($i++));
        $enc3 = this.base64.indexOf($input.charAt($i++));
        $enc4 = this.base64.indexOf($input.charAt($i++));
        $output += String.fromCharCode(($enc1 << 2) | ($enc2 >> 4));
        if ($enc3 != 64) $output += String.fromCharCode((($enc2 & 15) << 4) | ($enc3 >> 2));
        if ($enc4 != 64) $output += String.fromCharCode((($enc3 & 3) << 6) | $enc4);
    } while ( $i < $input . length );
    return $output;
}
};

var Hex = {
hex: "0123456789abcdef",
encode: function($input) {
    if (!$input) return false;
    var $output = "";
    var $k;
    var $i = 0;
    do {
        $k = $input.charCodeAt($i++);
        $output += this.hex.charAt(($k >> 4) & 0xf) + this.hex.charAt($k & 0xf);
    } while ( $i < $input . length );
    return $output;
},
decode: function($input) {
    if (!$input) return false;
    $input = $input.replace(/[^0-9abcdef]/g, "");
    var $output = "";
    var $i = 0;
    do {
        $output += String.fromCharCode(((this.hex.indexOf($input.charAt($i++)) << 4) & 0xf0) | (this.hex.indexOf($input.charAt($i++)) & 0xf));
    } while ( $i < $input . length );
    return $output;
}
};

var RSA = {

getPublicKey: function($modulus_hex, $exponent_hex) {
    return new RSAPublicKey($modulus_hex, $exponent_hex);
},

encrypt: function($data, $pubkey) {
    if (!$pubkey) return false;
    $data = this.pkcs1pad2($data, ($pubkey.modulus.bitLength() + 7) >> 3);
    if (!$data) return false;
    $data = $data.modPowInt($pubkey.encryptionExponent, $pubkey.modulus);
    if (!$data) return false;
    $data = $data.toString(16);
    if (($data.length & 1) == 1) $data = "0" + $data;
    return Base64.encode(Hex.decode($data));
},

pkcs1pad2: function($data, $keysize) {
    if ($keysize < $data.length + 11) return null;
    var $buffer = [];
    var $i = $data.length - 1;
    while ($i >= 0 && $keysize > 0) $buffer[--$keysize] = $data.charCodeAt($i--);
    $buffer[--$keysize] = 0;
    while ($keysize > 2) $buffer[--$keysize] = Math.floor(Math.random() * 254) + 1;
    $buffer[--$keysize] = 2;
    $buffer[--$keysize] = 0;
    return new BigInteger($buffer);
}
};

function getPwd(password,mod,exp) {
// var mod = mod;
// var exp = exp;
var pubKey = RSA.getPublicKey(mod, exp);
var encryptedPassword = RSA.encrypt(password, pubKey);

return encryptedPassword;

}

steam.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# author： 青城子
# datetime： 2021/8/31 20:43 
# ide： PyCharm

import requests
import execjs


class Steam:
    def __init__(self, password="123456", username="tian@qq.com", exe_function="getPwd", ):
        """
        默认逆向的密码：123456，爬虫调用时根据具体情况传入自己的密码
        默认username，爬虫调用时根据具体情况传入自己的登录账号
        默认steam.js中的执行函数名getPwd,若steam.js中函数名不是getPwd，传入具体函数名即可

        :param password: 默认密码
        :param exe_function: 默认steam.js中执行的函数名
        :param username: 默认登录名
        """
        self.url = "https://store.steampowered.com/login/getrsakey/"
        self.data = {
            "donotcache": "1630411448195",
            "username": username,
        }
        self.headers = {
            "User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/84.0.4147.105 Safari/537.36",
        }
        self.node = execjs.get()
        self.password = password
        self.exe_function = exe_function

    def get_mod_exp(self):
        """
        获取mod、exp
        :return:
        """
        res_json = requests.post(url=self.url, headers=self.headers, data=self.data).json()
        mod = res_json.get("publickey_mod")
        exp = res_json.get("publickey_exp")
        return mod, exp

    def reverse_engineer(self):
        """
        执行js获取逆向后的pwd
        :return:pwd
        """
        mod, exp = self.get_mod_exp()
        ctx = self.node.compile(open("../static/steam.js", encoding="utf-8").read())
        func_name = "{0}('{1}','{2}','{3}')".format(self.exe_function, self.password, mod, exp)
        pwd = ctx.eval(func_name)
        return pwd


if __name__ == '__main__':
    obj = Steam()
    rest = obj.reverse_engineer()
    print(rest)

源码地址：https://gitee.com/tianxiang2018