机器学习---算法---逻辑回归
转自:https://blog.csdn.net/ustbbsy/article/details/80423294
1 引言
最近做一个项目,准备用逻辑回归来把数据压缩到[-1,1],但最后的预测却是和标签类似(或者一样)的预测。也就是说它的predict的结果不是连续的,而是类别,1,2,3,...k。对于predict_proba,这是预测的概率,但概率有很多个,数目为训练集类别(label)的个数。逻辑回归的原理,就是取出最大概率对应的类别。
所以逻辑回归,不是回归,而是分类器,二分类,多分类。
逻辑回归,是一个很有误导性的概念。
这是个人最近的体会,入门的读者请忽略。
2 线性回归
先说一下,一般模型的训练和预测过程:
1,训练:通过训练数据来训练模型,也就是通常我们所说的学习过程,即确定模型的参数。
2, 预测:训练过后,模型参数确定,有预测数据输入,就会得到一个结果。
常见的线性回归y=wx+b,我们通过训练集来训练出我们的模型,也就是得到我们的模型参数w,b,这样,我们的直线或者超平面(x是多维的)就确定了。接着,对于测试集,来了一个数据x,w,b已经学习出来了,带入y=wx+b,就会得到一个y值,也就是我们的预测值。注意, 它是浮点数。
这里得到的y为什么叫回归呢,因为y不是类别(label)中的一个,它是预测出来的实数(大部分是小数)。
有的同学可能不理解什么是回归?我解释一下:
首先,需要明白二分类,类别/标签/label是二值,{0,1}或{-1,1},总之它的类别数两个。相信你已经知道多分类了,就是类别是多值的,{0,1,2,3,4}等,这是5类。那么回归是什么你呢。回归的取值,就不是像分类这样取整数了,它是小数,浮点数,是连续的,例如(0,1)之间的取值等。
3 逻辑回归
前面已经说了,虽然它不是回归,但是名字已经确定了,大家还是这么叫的。
前面的线性回归,我们已经得到y=wx+b。它是实数,y的取值范围可以是(负无穷,正无穷)。现在,我们不想让它的值这么大,所以我们就想把这个值给压缩一下,压缩到[0,1]。什么函数可以干这个事呢?研究人员发现signomid函数就有这个功能。所以,他们就尝试着,用signomid函数搞一搞这个y。
sigmoid的函数如下:
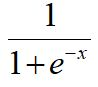
sigmoid的图像如下:
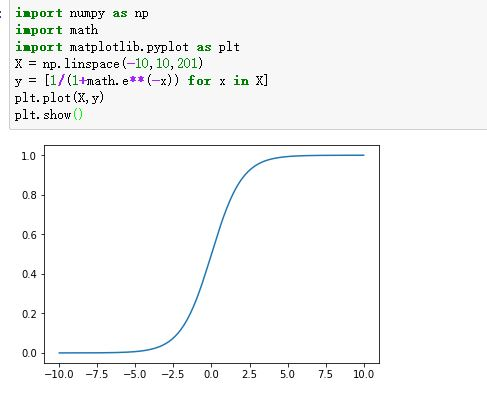
压缩,就是把y=wx+b带入sigmoid(x)。把这个函数的输出,还定义为y,即:
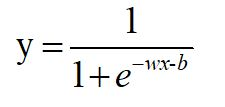
这样,y就是(0,1)的取值。
把这个式子变换一下:
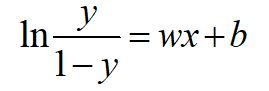
4 损失函数
损失函数,通俗讲,就是衡量真实值和预测值之间差距的函数。所以,我们希望这个函数越小越好。在这里,最小损失是0。
以二分类(0,1)为例:
当真值为1,模型的预测输出为1时,损失最好为0,预测为0是,损失尽量大。
同样的,当真值为0,模型的预测输出为0时,损失最好为0,预测为1是,损失尽量大。
所以,我们尽量使损失函数尽量小,越小说明预测的越准确。
这个损失函数为:
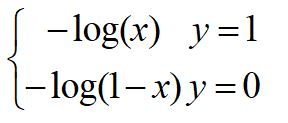
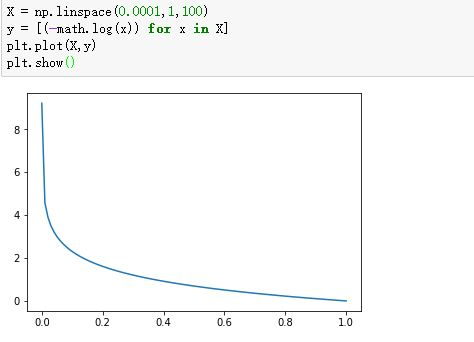
我们看看这个函数的图像:
-log(x):
-log(1-x):
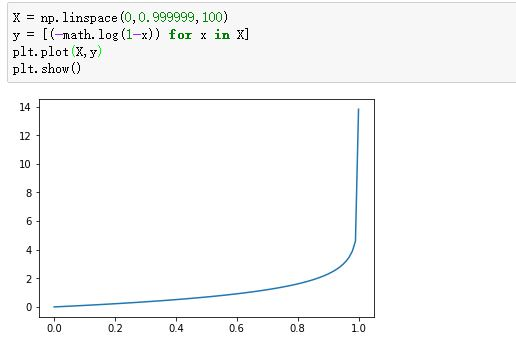
所以,我们压缩之后,预测y在0-1之间。我们利用这个损失函数,尽量使这个损失小,就能达到很好的效果。
我们把这两个损失综合起来:

y就是标签,分别取0,1,看看是不是我们前面写的那两个损失函数。
对于m个样本,总的损失:
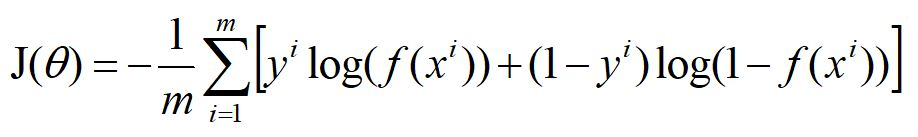
这个式子中,m是样本数,y是标签,取值0或1,i表示第i个样本,f(x)表示预测的输出。
不过,当损失过于小时,也就是模型能拟合全部/绝大部分的数据,就有可能出现过拟合。这种损失最小是经验风险最小,为了不让模型过拟合,我们又引入了其他的东西,来尽量减小过拟合,就是大家所说的结构风险损失。
结构经验风险常用的是正则化,L0,L1,L2正则化




