现代密码学——原理与协议 读书笔记
第7章 数论和密码学困难性假设
知识点
素数、模运算、群、子群、群同构、中国剩余定定理、生成随机素数、素数判定、因子分解假设、RSA假设、循环群、生成元、离散对数和Diffie—Hellman假设、椭圆曲线群、单向函数和置换、构造抗碰撞的散列函数
专业术语
non-trivial factor:非平凡因子 除1和自身之外的因子
prime:素数 composite:合数
division with remainder:带余除法
gcd: greatest common divisor
relatively prime:互素
Modular Arithmetic:模算术
reduction modulo N:模N的消减运算
congruent modulo N/Congruence modulo N:模N同余
equivalence relation:等价关系 reflexive、symmetric、transitive:自反、对称、传递
(multiplicative) inverse:(乘法)逆元 b invertible modulo N:b模N可逆
binary operation:二元运算 group:群
Closure:封闭性 Existence of an Identity:存在单位元 Existence of Inverses:存在逆元
Associativity:结合律 Commutativity:交换律 abelian:阿贝尔群
finite group:有限群 the order of the group:群的阶
subgroup:子群 trivial subgroups:平凡子群 strict subgroup:严格子群
cancelation law:消去律
permutation:置换 Group Isomorphisms:群同构
bijection:双射
Chinese Remainder Theorem:中国剩余定理
factoring:因子分解 factorization:因数分解
trial division:试除法
one-way function:单向函数
cyclic groups:循环群
iff:当且仅当
Discrete Logarithm:离散对数
discrete logarithm of h with respect to g:关于g的h的离散对数
computational Diffie-Hellman (CDH) problem:计算Diffie-Hellman问题
decisional Diffie-Hellman (DDH) problem:判定Diffie-Hellman问题
quadratic residue modulo p:模p平方剩余
elliptic curves:椭圆曲线
重要/疑难定理
中国剩余定理从具体到抽象
素数判定
Q&A
群的阶和群中元素的阶的定义?
群的阶:群中元素的个数
群中元素的阶:
离散对数实验
?
答:双数线表示一个范数,1阶范数相当于比特长度,表示q是n比特长
括号中后面这个条件确保了方程没有重根如何得到的?
可由三次方程重根判别式推导化简得到
[三次方程求根](三次方程_百度百科 (baidu.com))
one way function 和 公钥密码 的关系?
答:公钥密码的因子分解和离散对数的困难性假设意味着单向函数的存在性。
第8章 因子分解和离散对数算法
知识点
因子分解算法(p-1方法、Rho方法、二次筛选法)
计算离散对数的算法(小步大步法、Pohlig-Hellman算法、索引演算方法)
专业术语
quadratic sieve algorithm:二次筛算法
general number field sieve:通用数域筛法
quadratic residue modulo N:模N二次剩余
heuristically:启发式地
base:底数
baby-step/giant-step method:小步/大步法
index calculus method:索引演算方法
polylog:多重对数函数/多对数函数
Q&A
启发式地证明xxx 如何理解?
类似于公理、容易推导
polylog函数:多重对数函数/多对数函数?多项式对数函数?
攻击算法 和 公钥密码算法安全强度、安全参数的关系?
困难问题是什么?什么样的问题是困难的?困难程度如何判断?困难程度和安全强度的关系?困难问题的强弱怎么判别?
《可证明安全算法与协议》P17
第四个知识点 P类复杂问题 - WangZhuo2000 - 博客园 (cnblogs.com)
第五个知识点 复杂性为NP类是什么意思 - WangZhuo2000 - 博客园 (cnblogs.com)
P、NP、NPC和NP-Hard相关概念的图形和解释_Paul_Huang的专栏-CSDN博客
P问题:确定性图灵机多项式时间可以求解的问题
NP问题:非确定性图灵机多项式时间可以求解的问题
第9章 对称密钥管理和公钥革命
知识点
对称密钥加密的局限性、密钥分配中心、公钥革命、Diffe-Hellman密钥交换
专业术语
key distribution center(KDC):密钥分配中心
Q&A
如何保证用户公开的公钥一定是该用户的公钥?
普通数字签名、散列后数字签名、Lamport的"一次性签名方案"、公钥基础设施(PKI)
第10章 公钥加密
知识点
公钥加密简介、多重加密、混合加密、RSA加密、EI Gamal加密、选择密文攻击的安全性、陷门置换
专业术语
asymmetric:非对称的
lemma:引理
Q&A
消息向量的具体含义?
DL和DDH,DL和CDH,DDH和CDH区分,困难问题的难度强弱?
《公钥密码学:设计原理与可证安全》p62
DLP:尽管有次指数级的算法,但是没有证明不存在多项式时间内解决DLP的方法.
CDH:CDH是和DLP相关的,但是哪个更难呢?如果我能有效率的解决DLP,那么我就可以找出a,然后轻松的计算出g^(ab)就像Bob做的那样,因此我们就解决了CDH.所以我们说能解决DLP那么一定能解决CDH,这就是说DLP至少和CDH一样难.
DDH:而且很明显,如果对手能解决CDH问题,那么它可以有效率的解决DDH,因为它已经可以得到gabgab的值.这意味着,CDH至少和DDH一样难.
这就是我们这篇中讨论的三个问题,我们给出了一个简明的证明对他们的困难性进行排序:DLP最难,然后是CDH,最后是DDH.就像我们看到的那样,DLP有时候是简单的,会让CDH和DDH都变简单.因此群GG和生成器gg的选择在做密码学的时候是十分重要的!
第11章 其他公钥加密方案
知识点
Goldwasser-Micali加密方案、Rabin加密方案、Paillier加密方案
Q&A
Rabin加密方案中的 lsb(x)是什么意思?
第12章 数字签名
知识点
数字签名简介、RSA签名、Hash and Sign、Lamport的"一次性签名方案"、基于Chain的签名、基于Tree的签名、数字证书和公钥基础设施
第13章 随机预言机模型中的公钥密码系统
知识点
随机预言机方法学、随机预言机模型中的公钥加密、随机预言机模型中的签名

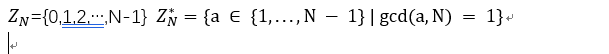



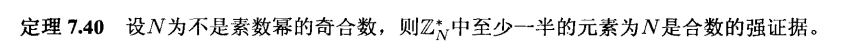


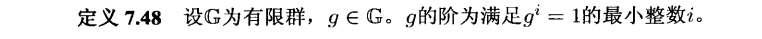

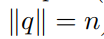
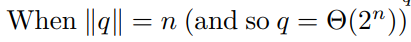






【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步