配电网可靠性模糊建模的精确化方法研究
0 引言
随着南宁电网规模的不断扩大，电力资源进一步优化配置，以及客户全方位服务工作的全面深化开展，电网的可靠运行迎来了新的挑战。配电网作为电力系统面向用户的最后一个环节，它对用户供电可靠性具有最直接的影响。配电用户对于供电可靠性要求越来越高，供电局内部对于供电可靠性的考核也愈发严格。如何能够做到事前评估、事中预防、事后统计，从规划到运行各个阶段实现对可靠性的有效管理，从根本上提高配电网运行的可靠性水平，具有重大的理论研究和现实意义。
伴随着电网规模的扩大，每次停电故障可能造成的平均负荷损失也随之增大。因此，改进可靠性预测算法，优化可靠性建模方法，提高电网可靠性，确保电网紧急安全运行已成为配电网运行当前面临的紧迫问题。本文提出一种配电网可靠性模糊建模的精确化方法，综合考虑电网各种因素的内在联系以及网络特性的质变体现到电网的拓扑接线，从而克服通常采用与负荷预测相似的方法进行可靠性预测时的各种缺点。
1 配电网可靠性预测
通常根据数据来源的精确性和接口的方便性，将未来电网的可靠性采用模糊建模的方式进行预测，数据来源于可靠性管理系统、配网详细规划以及检修计划、基建计划、技改计划和业扩计划。
现有的可靠性评估预测算法报道很少，本文借鉴负荷预测的相关分析法对可靠性指标进行预测。
1.1 传统可靠性预测算法
可靠性预测相关分析法的计算模型如下：
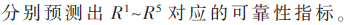
1.2 模糊建模算法的优缺点
可靠性预测模糊建模算法的优点是：
（1）建模简单：只需每年滚动输入若干电网相关参数和计划停运等相关信息即可进行可靠性预测。
（2）求解简单：方程规模小，求解速度快。
可靠性预测模糊建模算法的缺点是：
（1）需要大量的历史数据：从可靠性预测算法模型来看，最少需要3~5年的电网可靠性历史数据、电网特性数据和计划停运数据，如果在一个新的地方开展可靠性预测，很多历史数据由于获取困难，而导致这种预测方法的精确度很差。
（2）无法体现不可量化因素对建模的影响：采用模糊建模方法只能考虑电网的可量化因素，而不可量化因素很难体现。
（3）各相关因素的内在联系无法体现：比如一个手拉手或多联络接线方式占100%的网络，其可靠性指标与线路的故障和计划停运因素相关度较小，而这样的网络在模糊建模时线路主干线长度并不会有多大的影响，但模型中考虑这个因素时所需的历史数据就需要更多才能表现出这种内在的关系对预测结果的影响。
（4）只能体现量变，无法体现质变：当可靠性指标变化平衡，电网特性参数和计划停电情况变化平衡的情况下，采用这种模型预测精确较高；但电网特性发生本质上的变化时，可靠性指标会发生质的飞跃，这时模型的精度就会很低。
2 可靠性模糊建模的精确化方法
鉴于采用类似于负荷预测的方法进行可靠性预测所面临的问题，结合可靠性研究经验，本文开创性地提出一种可靠性模糊建模的精确化方法。
可靠性无法精确建模的原因是网络拓扑结构不确定，或由于建立详细的网络拓扑结构所需的人工工作量过大，限制了这种方法的使用。在采用模糊建模时电网的特性参数是在电网详细规划报告中容易提取的数据，包括电缆平均长度X1（km/条），架空线平均长度X2（km/条），绝缘化率X3（%），可转供电率X4（%），环网率X5（%），架空线平均分段数X6（段），电缆平均分段数X7（段），平均每条干线分支数X8（条），平均分支线长度X9（km/条），平均每条干线配电变压器台数X10（台/条），平均每条支线配电变压器台数X11（台/条），配电变压器平均容量X12（kVA/台），配电变压器平均负载率X13（%），主干线平均负载率X14（%），电缆线路型号X15，架空线路型号X16。
为克服传统可靠性预测方法所表述的问题，可将上述平均指标具体化成一个特定的小规模网络，这个网络具有上述电网的参数特性，然后对这个特定的网络接线采用精确化可靠性评估的方法进行评估。
从可行性上来看，由于网络建模规模小，采用人工搭建电网可靠性仿真计算模型所耗费的时间较少，切实可行。
从合理性上来看，当小型网络具有大网络的平均电网特性后，这个网络每个负荷点的可靠性数据就与大网络各个负荷点的平均可靠性数据近似。也就是说两个电网的用户平均停电次数和用户平均停电时间是近似的，从系统的7项可靠性指标的求解公式来看，这两项指标相近，其他指标也是相近似的，因而合理。
从效益性方面来看，由于采用与负荷预测相似的方法进行可靠性预测时，电网特性参数每个地区不尽相同，其蕴涵的规律也是不一样的，而可靠性指标的变化蕴涵在这些数据中，因此，用于可靠性预测的历史库不具有普适性。而采用模糊建模的精确化方法，可建立大量的电网模型库，可靠性指标变化蕴涵的特点具体化成特定的网络拓扑接线数据，不仅表现为数据表面的变化，电网各因素的内在联系和网络特性的质变通过可靠性的精确建模的计算来体现，因此这种模型库更具有普适性，其规模效益非常明显。
3 精确化方法的实施方案
3.1 两种实施方案
可靠性模糊建模的精确化实施方案可参考以下两种方式。以广西供电局为例，分别说明两种方式的具体实施流程。
（1）方式一：适用于技术力量薄弱的供电局。这种方式无需该公司专门配置可靠性技术人员，可靠性电网模型库由技术力量雄厚的广西供电局统一建模、发布，分区供电局的技术人员只需要按要求录入数据，即可实现可靠性预测。
具体实施流程如图1所示。
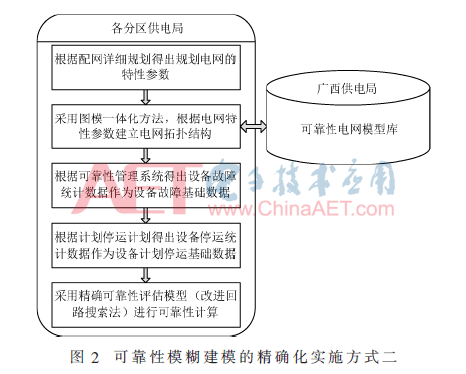
（2）方式二：适用于可配置专门技术人员进行可靠性评估的分区供电局。这种方式由可靠性评估的技术人员按照电网特性参数采用图模一体化的方式进行电网建模。这种方式的优点是评估结果更加精确，而且可为广西供电局的可靠性电网模型库进行扩充，若每年每个供电局为省网公司提供一个可靠性电网模型，那么广西供电局的可靠性电网模型库将非常丰富。这种方式为可靠性评估预测及辅助决策系统的广泛使用提供了灵活性。
具体实施流程如图2所示。
3.2 建模实例
经过反复建模、计算并与实际网络可靠性精确计算结果相比较，得出如下模糊建模所需的电网特征及参数如下：
· 电缆化率。
· 可转供电率。
· 环网率。
· 主干线平均长度。
· 主干线平均分段数。
· 平均每条干线分支数，分支线平均长度。
· 主干线上配变总台数，分支线上配变总台数。
· 配电变压器平均容量，配电变压器平均负载率。
· 电缆、架空线路型号。
采用图模一体化方法在电力矢量图编辑系统上进行建模，建模过程以下例进行说明。
某电网电缆平均长度X1=3.1（km/条），架空线平均长度X2=3.5（km/条），电缆化率X3=92（%），可转供电率X4=85%，环网率X5=90（%），架空线平均分段数X6=2.5（台），电缆平均分段数X7=2.5（台），平均每条主干线分支数X8=1（条），平均分支线长度X9=1.7（km/条），平均每条干线配电变压器台数X10=13（台/条），平均每条分支线配电变压器台数X11=6（台/条），配电变压器平均容量X12=400（kVA/台），配电变压器平均负载率X13=58（%）。电缆型号为YJV-300，架空线路型号为LGJ-185。
根据以上电网特性参数，由可靠性技术人员在可靠性评估预测系统中的图形建模平台上绘制100条10kV主干线，6条电缆为单辐射接线，4条架空线为单辐射接线，72条电缆为手拉手接线，4条架空线为手拉手接线，4条混合线为手拉手接线，9条电缆为多联络接线，1条混合线为多联络接线，主干线长度为3.5 km，50条线路分段开关数为2台，50条线路分段开关数为3台（设分段数为2的线路数为a，分段数为3的线路数为b，则2×a+3×b=100×2.5，可得a=50，b=50），每条干线绘制一条分支线，分支线长度1.7 km，电缆型号设为YJV-300，架空线路型号设为LGJ-185。50%的干线路所带配电变压器13台，50%的干线路所带配电变压器14台，每条支线所带配电变压器参数6台，每台配电变压器容量为400 kVA，每台配变所带负荷为400×58%×0.95=220.4 MW，功率因数取0.95。
建模完成后，录入设备故障基础数据和计划停电数据，即可算出模拟电网的可靠性。根据以上电网特性参数，通过精确化的模糊建模，得出的可靠性指标应该与原电网可靠性指标接近。需要注意的是：对于平均性质的可靠性指标，如用户平均停电次数AITC-1（次/户）、用户平均停电时间AIHC-1（小时/户）、平均供电可用率指标RS-1（%），这些指标是接近的；但对于总量性质的可靠性指标，如系统总的电量不足指标ENSI（MWh/年）、系统总的停电损失LOSS（万元/年），这些应该与两个电网的总用户数、总负荷数相关，如果两个电网负荷相差10倍，那么这两项表示总量的指标在同样可靠性水平下也应该相差约10倍。
从工作量上看，通常一个电网都有几千上万条10 kV馈线，采用这种模拟电网的建模方式，其工作量可大约减少为原来的1/100。此外通过合理设计图模一体化建模系统，可大量减少线路的绘制和参数录入工作量。随着网局层面的可靠性电网模型库的建立，这样的建模工作量将会逐步减少，其累积效益也将会逐步体现。
4 结论
随着终端用户对电能质量的要求越来越高以及供电部门对于供电可靠性的考核也愈发严格，提升配电网的安全运行、供电可靠性具有重要的意义，同时，配电网的可靠性预测技术和方法也备受关注。本文通过分析传统可靠性预测算法的优缺点着手，结合可靠性研究经验，开创性地提出一种可靠性模糊建模的精确化方法。详细阐述了可靠性模糊建模的精确化方法以及实施方案和建模实例，在克服传统可靠性预测方法缺点的基础上，实现配电网可靠性高效率高精度预测。本文的精确化方法为配电网设计、改造、运行和维护提供了详细的参考，具有一定的实际意义。
参考文献
[1] 郭谋发.配电网自动化技术[M].北京：机械工业出版社，2012.
[2] KERSTING W H.配电系统建模与分析（第三版）[M]. 王承民，王冰，衣涛，等，译. 北京：机械工业出版社，2015.
[3] DL/T 1563-2016，中压配电网可靠性评估导则[S].北京：国家能源局，2016.
[4] 陶顺，肖湘宁，刘晓娟.电压暂降对配电系统可靠性影响及其评估指标的研究[J].中国电机工程学报，2005,25(21):63-69.
[5] 胡珊珊，肖先勇，魏晓天.考虑系统元件故障不确定性的电压暂降盲数评估[J]. Transmission & distribution Engineering & Technology, 2013,2(1):11-16.
[6] 梁惠施，程林，刘思革．基于蒙特卡罗模拟的含微网配电网可靠性评估[J]．电网技术，2011，35(10)：76-81.
[7] 徐荆州，李扬．基于GO法的复杂配电系统可靠性评估[J]．电工技术学报，2007，21(1)：149-153.
[8] 杨莳百，戴景宸，孙启宏．电力系统可靠性分析基础及应用[M]．北京：水利水电出版社，1986.
[9] 王敬敏，施婷．智能配电网评估指标体系的构建[J]．华北电力大学学报，2012，39(6)：65-70.
[10] 袁兆祥，孔祥玉，赵帅．分布式电源接入配电系统可靠性分析方法[J]．电力系统及其自动化学报，2013，25 (4)：112-116.
[11] 邱生敏．配电网可靠性评估方法研究[D]．广州：华南理工大学，2012.
