leetcode 1252. Cells with Odd Values in a Matrix
Given n and m which are the dimensions of a matrix initialized by zeros and given an array indices where indices[i] = [ri, ci]. For each pair of [ri, ci] you have to increment all cells in row ri and column ci by 1.
Return the number of cells with odd values in the matrix after applying the increment to all indices.
Example 1:
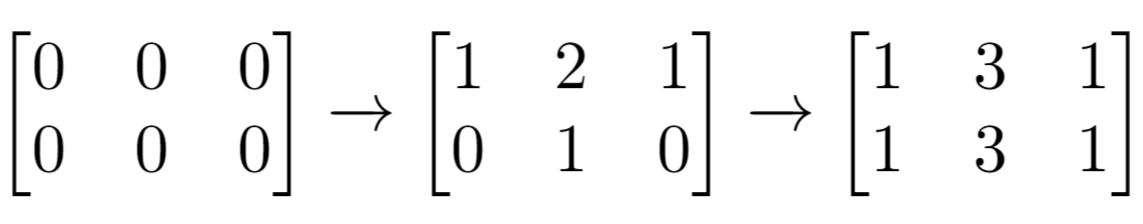
Input: n = 2, m = 3, indices = [[0,1],[1,1]] Output: 6 Explanation: Initial matrix = [[0,0,0],[0,0,0]]. After applying first increment it becomes [[1,2,1],[0,1,0]]. The final matrix will be [[1,3,1],[1,3,1]] which contains 6 odd numbers.
Example 2:
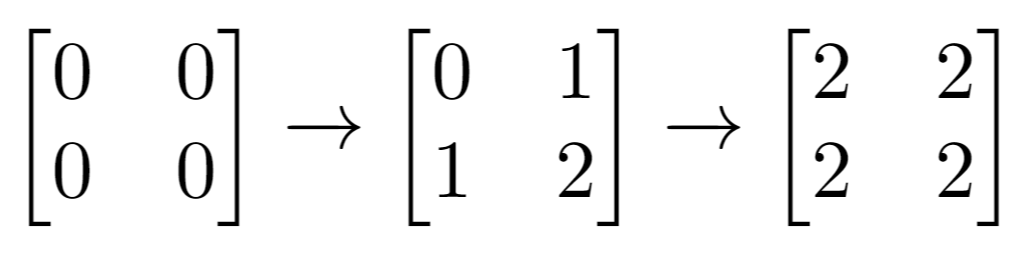
Input: n = 2, m = 2, indices = [[1,1],[0,0]] Output: 0 Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.
Constraints:
1 <= n <= 501 <= m <= 501 <= indices.length <= 1000 <= indices[i][0] < n0 <= indices[i][1] < m
题目大意:给定一个n行m列的零矩阵,对矩阵第indices[i][0]行所有元素加1,第indices[i][1]列元素加1. 最后统计矩阵中奇数的个数.
思路一:直接模拟。
1 int oddCells(int n, int m, vector<vector<int>>& indices) { 2 int cnt = 0; 3 vector<vector<int> > matrix(n, vector<int>(m, 0)); 4 for (int i = 0; i < indices.size(); ++i) { 5 int r = indices[i][0], c = indices[i][1]; 6 for (int j = 0; j < m; ++j) { 7 matrix[r][j] += 1; 8 } 9 for (int k = 0; k < n; ++k) { 10 matrix[k][c] += 1; 11 } 12 } 13 for (int i = 0; i < n; ++i) { 14 for (int j = 0; j < m; ++j) { 15 if ((matrix[i][j] & 1) == 1) 16 ++cnt; 17 } 18 } 19 return cnt; 20 }
时间复杂度:O(L*(n + m) + n * m)
空间复杂度:O(n * m)
思路二:我们判断矩阵(i,j)位置的奇偶性,只需要计算第i行加1的次数 + 第j列加1的次数,就是位置(i, j)的值,只需要判断它的奇偶性就行。进一步,我们只需要知道第i行加1的总次数的奇偶性,以及第j列加1的总次数的奇偶性,这两个数进行异或操作就行(同奇同偶,加起来肯定是偶数,异或结果为0,否则为1)
1 int oddCells(int n, int m, vector<vector<int>>& indices) { 2 int cnt = 0; 3 vector<int> row(n, 0), col(m, 0); //row(i)表示加1次数的值的奇偶性,0为偶数次,1为奇数次 4 for (auto ind: indices) { 5 int r = ind[0], c = ind[1]; 6 row[r] ^= 1; 7 col[c] ^= 1; 8 } 9 for (int i = 0; i < n; ++i) { 10 for (int j = 0; j < m; ++j) { 11 if (row[i] ^ col[j]) 12 ++cnt; 13 } 14 } 15 return cnt; 16 }
时间复杂度:O(L + n * m)
空间复杂度:O(n + m)
思路三:基于思路二,我们发现判断(i, j)位置的值是否为奇数,只用看row(i) ^ col(j), 如果(i, j)位置的数为奇数,则row(i)或者col(j)必有一个是奇数, 如果两个都是奇数,那么为偶数。
1 int oddCells(int n, int m, vector<vector<int>>& indices) { 2 int cnt = 0; 3 vector<int> row(n, 0), col(m, 0); //row(i)表示加1次数的值的奇偶性,0为偶数次,1为奇数次 4 for (auto ind: indices) { 5 int r = ind[0], c = ind[1]; 6 row[r] ^= 1; 7 col[c] ^= 1; 8 } 9 int cntRow = 0, cntCol = 0; 10 for (auto i:row) 11 cntRow += i; 12 for (auto i:col) 13 cntCol += i; 14 return m * cntRow + n * cntCol - 2 * cntRow * cntCol; 15 }
时间复杂度:O(L + n + m)
空间复杂度:O(n + m)
优化:
1 int oddCells(int n, int m, vector<vector<int>>& indices) { 2 int cntRow = 0, cntCol = 0; 3 vector<int> row(n, 0), col(m, 0); //row(i)表示加1次数的值的奇偶性,0为偶数次,1为奇数次 4 for (auto ind: indices) { 5 int r = ind[0], c = ind[1]; 6 row[r] ^= 1; 7 col[c] ^= 1; 8 cntRow += (row[r] == 1) ? 1 : -1; 9 cntCol += (col[c] == 1) ? 1 : -1; 10 } 11 return m * cntRow + n * cntCol - 2 * cntRow * cntCol; 12 }
时间复杂度:O(L)
空间复杂度:O(n + m)



