Whitening and Coloring transformations for multivariate gaussian data
1、介绍
这篇博客主要介绍如何白化(Whiten)符合正态分布的数据。在许多数据处理技术(如主成分分析、独立成分分析)之前,必须进行数据白化。
我们将一个d维均值为$\mu$,协方差矩阵为$\Sigma$的高斯随机变量$X$($X \in R^d$)的概率密度函数表示为
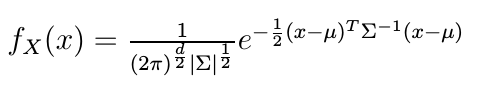
2、白化变换(Whitening Transform)
对于均值向量为$\mu$, 协方差矩阵为$\Sigma$的多元高斯随机变量$X$,我们想要将其变换成另一个随机变量,它的协方差矩阵为单位阵。这表明我们新的随机变量的各个成分是不相关的,并且方差为1.这个变换的过程成为白化。这个过程可以分解成两个步骤:1、对$X$的各个成分进行去相关。产生的数据可以看成是从一个协方差矩阵为对角阵的分布得到的。2、我们必须对各个成分进行缩放(scale),使其方差为1.
出于多种原因,强制统计独立性很有用。例如,在存在于多个维度的数据的概率模型中,当维度在统计上独立时,联合分布(可能非常复杂且难以描述)可以分解为许多更简单分布的乘积。强制所有尺寸具有单位方差也很有用。例如,缩放所有变量以使其具有相同的方差将对每个维度都具有同等重要性。
假如我们有数据矩阵$X$, 由n个K维的观测值组成($X \in R^{K \times n}$), 并且$X$已经中心化($X$的每一行已经减去其均值).协方差矩阵为
$\Sigma = Cov(X) = \mathbb E[X X^T]$
其中\mathbb E[X X^T] \approx \frac{X X^T}{n}
显然,协方差矩阵$\Sigma$是对称正定的(直接用定义可证明)。我们对协方差矩阵进行特征值分解
$\Sigma = \Phi\Lambda{\Phi}^{-1}$
其中$\Lambda$是$\Sigma$特征值组成的对角阵,$\Phi$的第i列向量是$\Lambda$从左上到右下第i个特征值对应的特征向量。另外$\Phi$的列向量是正交的,因此
${\Phi}^{-1} = {\Phi}^{T}$
我们令$Y={\Phi}^{T}X$,由于
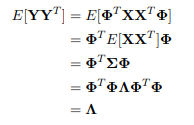
这表明,我们可以通过左乘协方差矩阵对应特征向量组成矩阵的转置将$X$变换成不相关的变量。
令$W=\Lambda^{-\frac{1}{2}Y=\Lambda^{-\frac{1}{2}\Phi^TX$, 由于
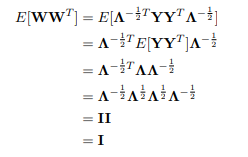
表明此时的W就是白化后的数据,即对原始数据先左乘协方差矩阵特征向量组成的矩阵进行去相关操作,再在左乘特征值对角阵的开根进行缩放(scale)操作。
3、例子
(matlab)
1 n = 1000; 2 convx = [10,-6;-6,5]; 3 mu = [0,0]; 4 5 S = mvnrnd(mu,convx,n)'; % 产生(2,1000)的样本 6 7 [phi, lam] = eig(convx); % 特征值分解,phi每一列是一个基向量 8 9 Y = phi' * S; %decorrelate 10 11 W = sqrt(lam) \ Y; %scale 12 13 figure; 14 subplot(131); 15 plot(S(1,:), S(2,:),'b.'); 16 axis square, grid 17 xlim([-10 10]);ylim([-10 10]); 18 title('original data'); 19 subplot(132); 20 plot(Y(1,:), Y(2,:),'b.'); 21 axis square, grid 22 xlim([-10 10]);ylim([-10 10]); 23 title('decorrelated data'); 24 subplot(133); 25 plot(W(1,:), W(2,:),'b.'); 26 axis square, grid 27 xlim([-10 10]);ylim([-10 10]); 28 title('whiten');
得到的图:
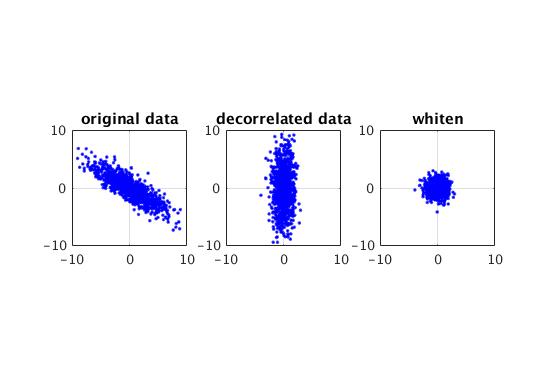
4、色彩化变换(Coloring transform)
色彩化变换是白化变换的逆变换,假设有数据矩阵$W$, 由n个K维的观测值组成($W \in R^{K \times n}$), W各列的向量各维是独立同分布的,单位方差。我们要将其变换为制定具有一定均值$\mu_1$和协方差矩阵$\Sigma_1$的高斯变量X。
对协方差矩阵进行特征值分解:$\Sigma_1 = \Phi\Lambda{\Phi}^{-1}$。
同理:
$X=\PhiY=\Phi\Lambda^{\frac{1}{2}W$
结合白化和色彩化变换,将白化后的数据,经过色彩化变换到符合另一分布的数据。
5、例子:
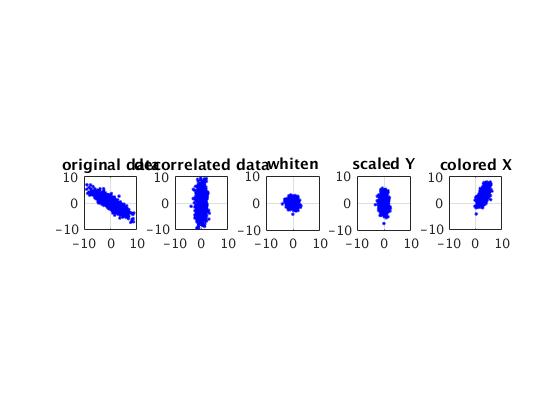
1 clc;clear all;close all; 2 n = 1000; 3 convx = [10,-6;-6,5]; 4 mu = [0,0]'; 5 6 S = mvnrnd(mu,convx,n)'; 7 [phi, lam] = eig(convx); 8 9 Y = phi' * S; 10 11 W = sqrt(lam) \ Y; 12 13 mu1 = [3, 3]; 14 conv = [1, 0.9;0.9, 3]; 15 [p, l] = eig(conv); 16 Y_1 = sqrt(l) * W; 17 18 S_ = p * Y_1; 19 S_r = S_ + mu1'; 20 21 figure; 22 subplot(151); 23 plot(S(1,:), S(2,:),'b.'); 24 axis square, grid 25 xlim([-10 10]);ylim([-10 10]); 26 title('original data'); 27 subplot(152); 28 plot(Y(1,:), Y(2,:),'b.'); 29 axis square, grid 30 xlim([-10 10]);ylim([-10 10]); 31 title('decorrelated data'); 32 subplot(153); 33 plot(W(1,:), W(2,:),'b.'); 34 axis square, grid 35 xlim([-10 10]);ylim([-10 10]); 36 title('whiten'); 37 subplot(154); 38 plot(Y_1(1,:), Y_1(2,:),'b.'); 39 axis square, grid 40 xlim([-10 10]);ylim([-10 10]); 41 title('scaled Y'); 42 subplot(155); 43 plot(S_r(1,:), S_r(2,:),'b.'); 44 axis square, grid 45 xlim([-10 10]);ylim([-10 10]); 46 title('colored X');
参考文献:
1、https://theclevermachine.wordpress.com/2013/03/30/the-statistical-whitening-transform/
3、http://sofasofa.io/forum_main_post.php?postid=1003324
4、https://stats.stackexchange.com/questions/326587/whitening-decorrelation-why-does-it-work
5、https://hadrienj.github.io/posts/Preprocessing-for-deep-learning/



