数据挖掘从入门到放弃（二）：决策树

“ 上篇内容介绍的是线性回归和逻辑回归模型，输入输出是连续值，分类模型的输出是一个有限集合，本篇介绍决策分类树算法”

 

决策树算法理解

决策树是直观运用概率分析的树形分类器，是很常用的分类方法，属于监管学习，决策树分类过程是从根节点开始，根据特征属性值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

比如说买瓜的时候，根据瓜的某些特征属性直观判断瓜的好坏，下图依次根据纹理清晰度、根蒂、色泽、触感4个进行分类，生活中我们会将某个最重要或最明显的分类属性放在第一位，然后是次重要属性，这很符合我们平常的判断思维，这就是决策树！

 

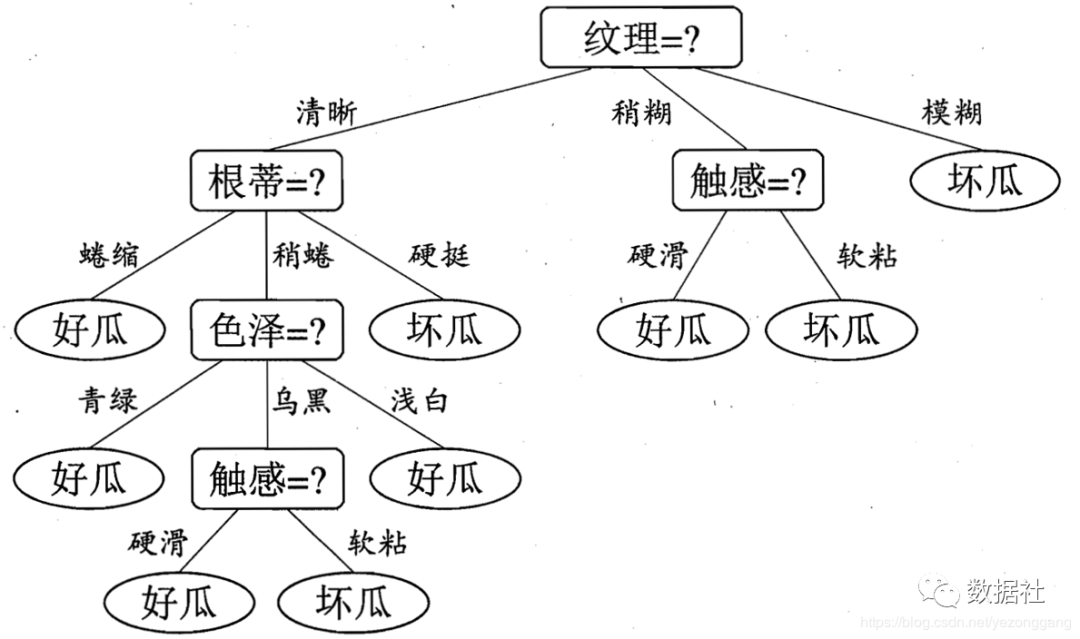
在特征属性非常大的时候，就出现了首选哪个特征属性进行分类？如何剪枝？分类的层次是多少？....系列问题，这些就是决策树构建的核心问题，而且不可能再通过生活直觉判，这时候就要运用数学思维。根据上面问题的不同解决方案，决策树又分为了ID3(熵增益)、C4.5(熵增益率)、CART几种同类算法。

熵增益（ID3）

通信层面，信息熵衡量信息的不确定性，信息熵越大表明信息越不准确，可以用信息熵的减少值来衡量信息的价值。在决策树模型中把信息确定性叫做熵增益，有了熵增益后，我们就可以根据熵增益来判断特征值的重要程度，从而选取最重要的特征作为第一次切分，再根据相同的方法用其他特征进行切分，直到得到得到每个划分的叶子节点。信息熵的定义是：

以某个特征属性值切分后子集熵的和称为条件A下的熵，也叫做条件熵，可以如下表示：

分类前的信息熵减去条件熵，得到熵增益：

比如说有以下数据集（相亲结果表lol..）

 

6条数据中相中（4个）与不想中（2个），暂且不关系如何进行分类，我们首先计算这个分类结果的信息熵：

其次，我们计算“富”属性的条件信息熵，6条数据中“富”与否各半，其中3个“富”都被分类到“相中”，3个“不富”都被分到“不想中”：

两者之差就是我们想要得到的熵增益：

计算各个特征属性的熵增益后，比较哪个熵增益最大，就选择该属性做第一分类特征。

 

熵增益率（C4.5）

按照熵增益最大准则的ID3算法，遇到全部都是非重复值（类似ID）属性容易造成过拟合，因为如果根据ID这个属性进行划分发现此时的熵增益是最大的：

信息增益率定义为：

其中info就是该特征属性中，属性值的信息熵：

按照上面的例子计算，“富”的增益率为：

剪枝处理

当训练数据量大、特征数量较多时构建的决策树过于庞大时，可能对训练集依赖过多，也就是对训练数据过度拟合。从训练数据集上看，拟合效果很好，但对于测试数据集或者新的实例来说，并不一定能够准确预测出其结果。因此，对于决策树的构建还需要最后一步--决策树的修剪，主要分为2种：预剪枝（Pre-Pruning）和后剪枝（Post-Pruning），这里先不讲。

鸢尾花(iris)分类模型

Iris 鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的哪一品种，数据集地址： https://github.com/yezonggang/iris

import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics 
 
baseUrl="C:\\Users\\71781\\Desktop\\2020\\ML-20200422\\iris\\"
iris_df=pd.read_csv(baseUrl+"iris.csv")
iris_df.head()
iris_df.describe()

　　

 数据分布探索：

# pandas 自带的散点图
iris_df.plot(kind="scatter", x="Sepal.Length", y="Sepal.Width")

　　

# seaborn 的联合分布图
sns.jointplot(x="Sepal.Length", y="Sepal.Width", data=iris_df, height=5)

　　

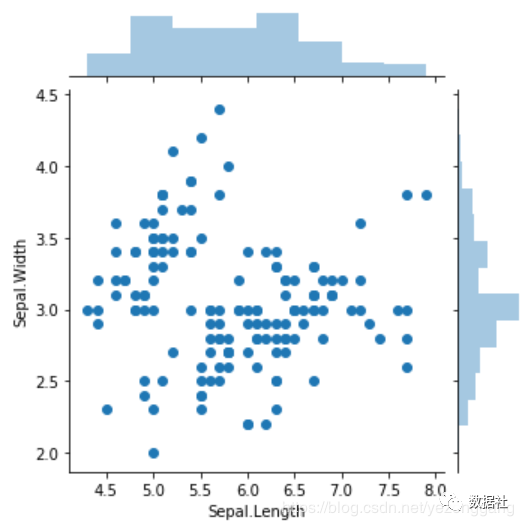
# 上面的两个散点图并不能显示每一个点所属的类别# 所以，接下来用 seaborn 的 FacetGrid 函数按照Species花的种类来在散点图上标上不同的颜色，hue英文是色彩的意思。

sns.FacetGrid(iris_df, hue="Species", height=5).map(plt.scatter, "Sepal.Length", "Sepal.Width").add_legend()

　　

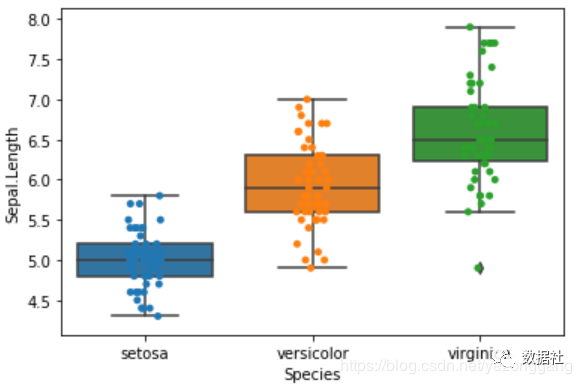
# 通过箱线图来查看单个特征的分布# 对 Numerical Variable，可以用 Box Plot 来直观地查看不同花类型的分布。

sns.boxplot(x="Species", y="Sepal.Length", data=iris_df)

　　

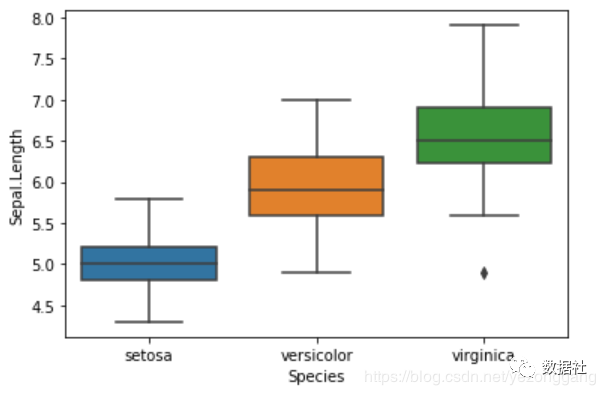
# 下面的操作，将每一个Species所属的点加到对应的位置，加上散点图，# 振动值jitter=True 使各个散点分开，要不然会是一条直线# 注意此处要将坐标图用ax先保存起来，这样第二次才会在原来的基础上加上散点图

ax = sns.boxplot(x="Species", y="Sepal.Length", data=iris_df)

ax = sns.stripplot(x="Species", y="Sepal.Length", data=iris_df, jitter=True, edgecolor="gray")

　　

# violinplot 小提琴图，查看密度分布，结合了前面的两个图，并且进行了简化# 数据越稠密越宽，越稀疏越窄

sns.violinplot(x="Species", y="Sepal.Length", data=iris_df, height=6) 
# sns.kdeplot == kernel density 核密度图（单个变量）

sns.FacetGrid(iris_df, hue="Species", height=6).map(sns.kdeplot, "Sepal.Length").add_legend() 
# pairplot 任意两个变量间的关系

sns.pairplot(iris_df, hue="Species", height=3)

　　

# 模型构建比较简单，关键是模型的调参

train_df=test_df=iris_df.sample(frac=0.8,replace=False, random_state=None)train_X=train_df.drop(['Species'],axis=1)train_Y=train_df['Species']

# 由于么有提供建模数据集，所以我们随机从样本集中选择40%的数据集

# replace=False 无放回的抽取

# random-state 数据不能重复

test_df=iris_df.sample(frac=0.9,replace=False, random_state=None)test_df.head() test_X=test_df.drop(['Species'],axis=1)

test_Y=test_df['Species'] 

model=DecisionTreeClassifier()model.fit(train_X, train_Y)

prediction = model.predict(test_X)

print('The accuracy of the Decision Tree is: {0}'.format(metrics.accuracy_score(prediction,test_Y)))

　　

总结

分类决策树总共有12个参数可以自己调整，这么多参数一个个记起来太麻烦，我们可以把这些参数分成几个类别：
    1）分类策略：有两个参数 ‘entropy’（熵） 和 ‘gini’（基尼系数）可选，默认为gini。
    2）max_depth（树的最大深度）：默认为None，此时决策树在建立子树的时候不会限制子树的深度。也可以设置具体的整数，一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。
    3）min_samples_split（分割内部节点所需的最小样本数）：意思就是只要在某个结点里有k个以上的样本，这个节点才需要继续划分，这个参数的默认值为2，也就是说只要有2个以上的样本被划分在一个节点，如果这两个样本还可以细分，这个节点就会继续细分
    4）min_samples_leaf（叶子节点上的最小样本数）：当你划分给某个叶子节点的样本少于设定的个数时，这个叶子节点会被剪枝，这样可以去除一些明显异常的噪声数据。默认为1，也就是说只有有两个样本类别不一样，就会继续划分。如果是int，那么将min_samples_leaf视为最小数量。如果为float，则min_samples_leaf为分数，ceil(min _ samples _ leaf * n _ samples)为每个节点的最小样本数。