常用 evaluation metrics

分类评估

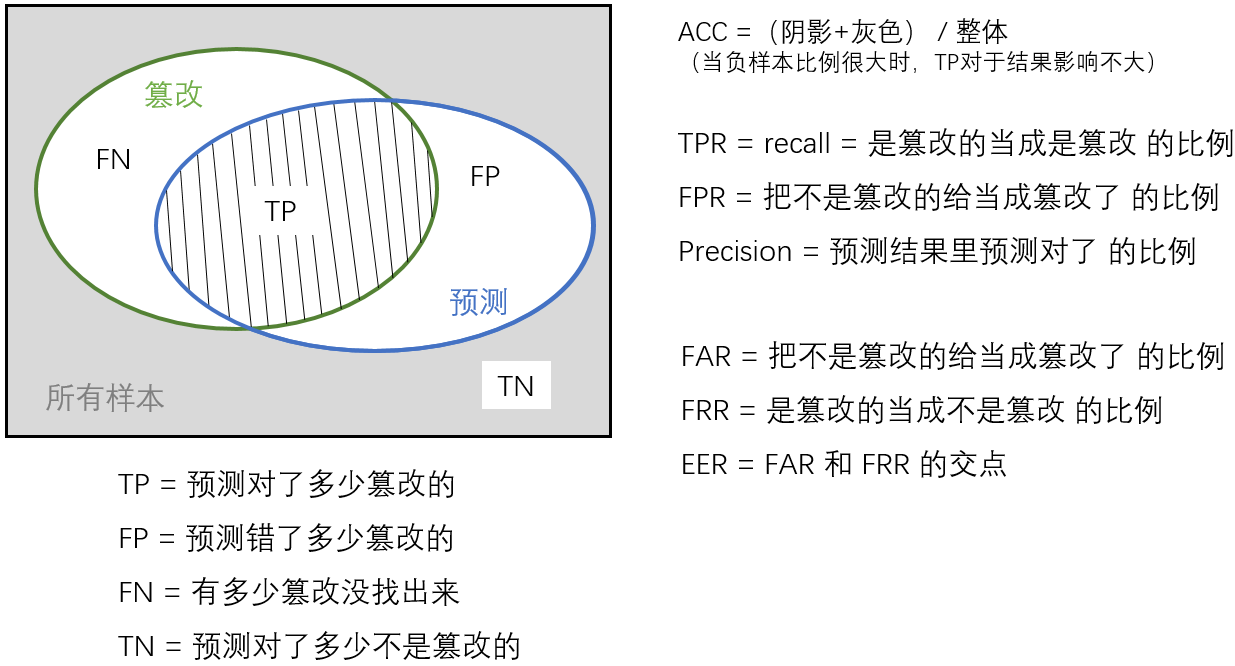
对于一个二分类问题，分类结果如下

预测\实际	正例	反例
正例	TP（真正例）	FP（假反例）
反例	FN（假正例）	TN（真反例）

1. accuracy 准确率

\[ACC=\frac{TP+TN}{TP+TN+FP+FN} \]

意为 预测对的样本数除以所有的样本数。实际没有用。

比如，正负样本不均衡时，假设负样本很少，即使所有样本预测为正样本，一个负样本都没有找出来，acc也很高。

2. TPR（recall）、FPR

TPR 真正例率 = recall 召回率 ：预测正确的正例占所有预测的正例的比率

是针对原样本而言的

\[TPR=recall=\frac{TP}{TP+FN} \]

FPR 假正例率：预测错误的正例占所有预测的反例的比率

\[FPR=\frac{FP}{FP+TN} \]

3. precision

precision 精确度：预测的正例中实际的正例比率

是针对预测结果而言的

\[precision=\frac{TP}{TP+FP} \]

4. EER

FAR 错误接受率 不该接受的样本里你接受的比例

\[FAR=\frac{FP}{FP+TN} \]

FRR 错误拒绝率 不该拒绝的样本里你拒绝的比例

\[FRR=\frac{FN}{TP+FN} \]

EER (Equal Error Rate )等错误率 :取一组0到1之间的等差数列，分别作为识别模型的判别界限，画出FFR和FAR的坐标图，交点就是EER值（FAR与FRR相等的点）

 

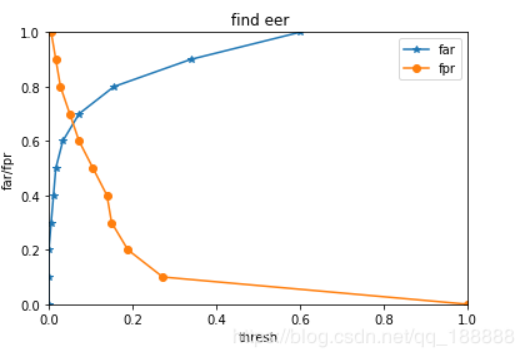
用检测篡改的思路看：

正样本是篡改区域。在生成的一个通道的二进制结果上计算。（还有多通道情况）

 

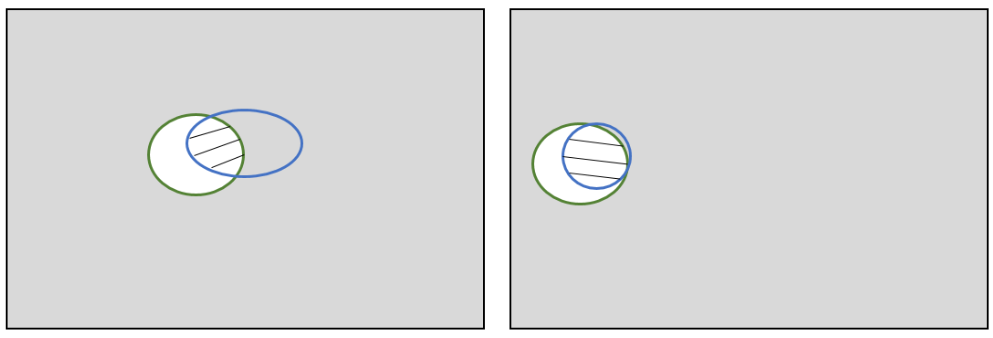
用极端例子（下图）解释 ACC 不好用：

检测篡改时会有总样本量大而篡改图像很少的情况，

假设阴影部分相同，负样本比例很大时，用 ACC 公式并不能很好描述篡改检测器的性能

5. f_score

理想状态下追求 precision 和 recall 都高，但事实上这两者在某些情况下是矛盾的。这样就需要综合考虑它们，F_score 是 precision 和 recall 的加权调和平均：

\[F=\frac{(\alpha^2 +1)Precision*Recall}{\alpha^2(Precision+Recall)} \]

当\(\alpha\)＜1时，代表精确率比召回率重要

当\(\alpha\)＞1时，代表召回率比精确率重要

当\(\alpha\)=1时，代表精确率和召回率都很重要，权重相同。即F1_score，

\[F1=\frac{2*Precision*Recall}{Precision+Recall} \]

\[\frac{2}{F1}=\frac{1}{precision}+\frac{1}{recall} \]

由于 precision 和 recall 越大越好，所以，F1 值越大越好

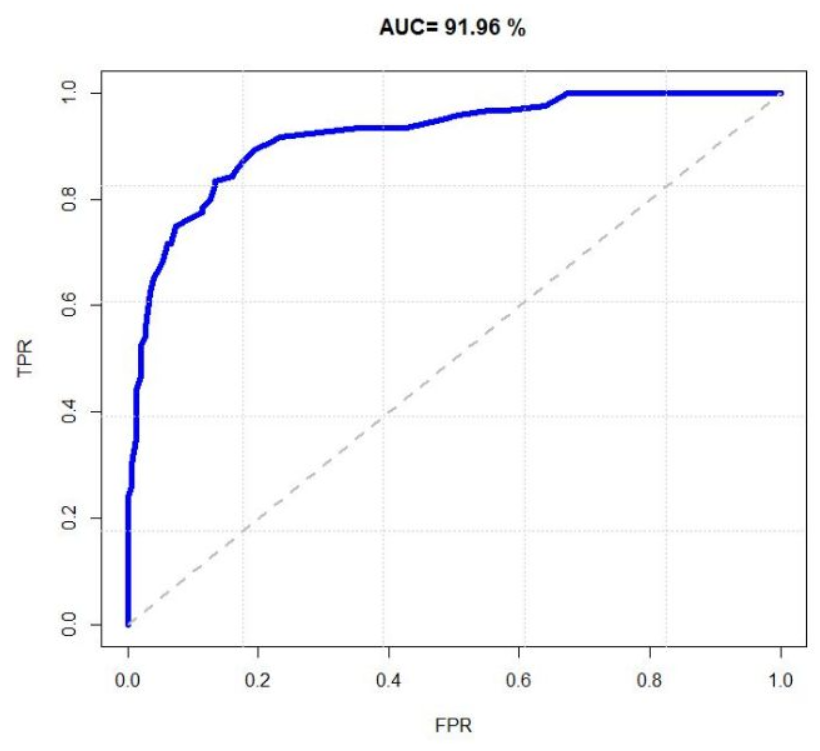
6. ROC curve

ROC的全名叫做Receiver Operating Characteristic （受试者特征），是一个画在平面上的曲线。

横坐标是false positive rate(FPR)，纵坐标是true positive rate(TPR)

当测试集中的正负样本分布发生变化时，ROC曲线能够保持不变，因此能进行客观地分析

7. AUC

AUC：Aera Under Curve，即ROC曲线下的面积，值域为（0,1）

AUC是一个数值

从AUC判断分类器的标准

• AUC=1，是完美分类器，通常不存在完美分类器
• 0.5＜AUC＜1，优于随机猜测
• AUC=0.5，跟随机猜测一样，相当于抛硬币
• AUC＜0.5，比随机猜测还差，但如果反预测而行，就优于随机猜测
• 

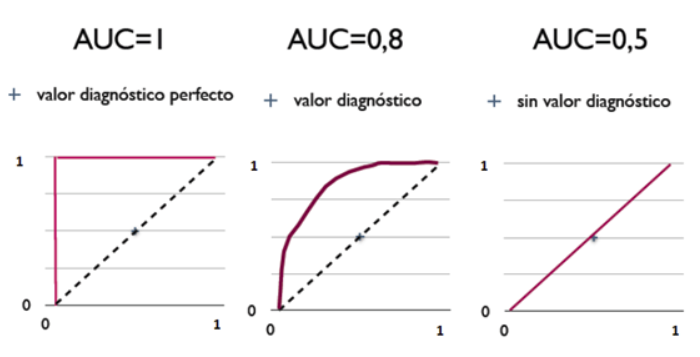
AUC值越大，对应的分类器的性能越好

举个栗子

假设有一个二分类模型，对 30 个样本分类，输出概率 p ，当 p＞0.5 时，预测的标签为1（真）

​                                                 

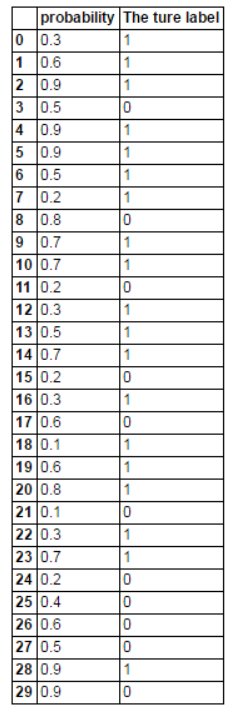
根据结果，得到混淆矩阵

预测 \ 实际	正例	反例
正例	13	6
反例	6	5

把预测概率从大到小排序

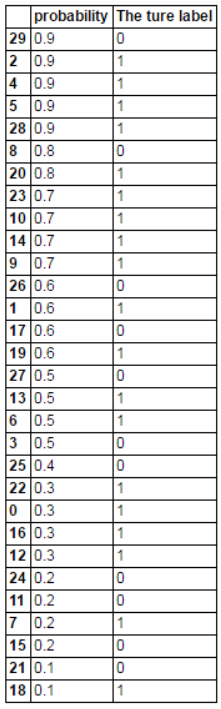
从上到下，依次计算 TPR 和 FPR

比如 4 号，p=0.9，在他之前的结果中，1个FP，2个TP，故TPR=2/(13+6)=0.11,FPR=2/(6+5)=0.09

比如26号，p=0.6，在他之前的结果中，3个FP，9个TP，故TPR=9/(13+6)=0.47,FPR=3/(5+6)=0.27

以此类推，得到（TPR,FPR）矩阵

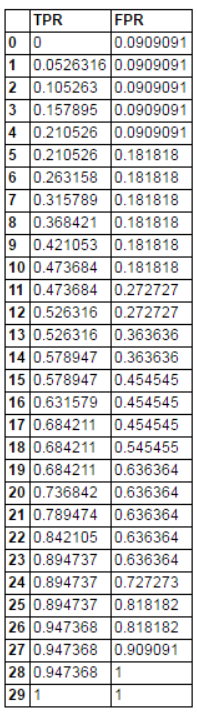
画 ROC 曲线

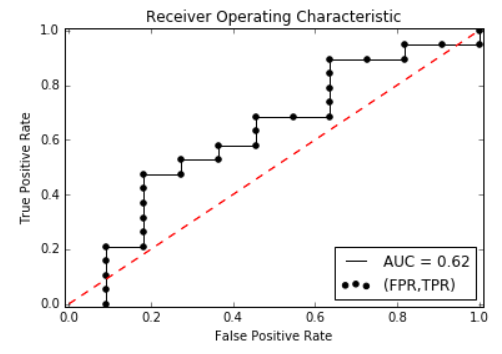
测试样本数量越多，曲线越光滑

黑色曲线下的面积即为 AUC

5. MCC

马修斯相关系数（Matthews correlation coefficient）

\[MCC=\frac{TP*TN-FP*FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} \]

MCC本质上是一个描述实际分类与预测分类之间的相关系数

它的取值范围为[-1,1]

取值为1时表示对受试对象的完美预测

取值为0时表示预测的结果还不如随机预测的结果

取值-1是指预测分类和实际分类完全不一致

MCC衡量不平衡数据集的指标比较好

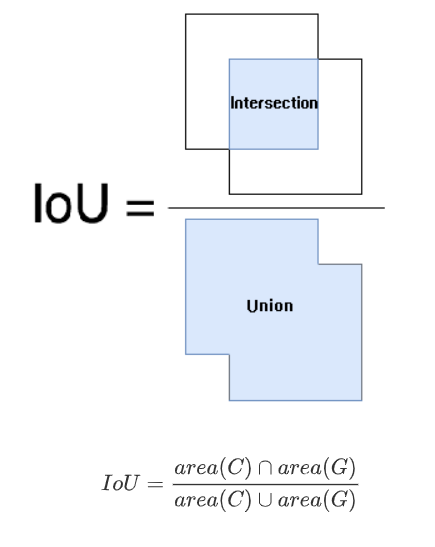
IoU

交并比 Intersection over Union ，是目标检测中的一个概念。

IOU表示产生的候选框（candidate bound）与原标记框（ground truth bound）两者的交集与并集的比值。

用上面那个图看是：阴影 / ( 阴影 + 白色 )

IoU 值越大越好

\[IoU=\frac{area(C)\cap area(G)}{area(C)\cup area(G)} \]

NMM

nimble mask metric

参考链接

https://www.plob.org/article/12476.html

https://blog.csdn.net/u014061630/article/details/82818112

https://blog.csdn.net/qq_18888869/article/details/84942224

[ROC]https://zhuanlan.zhihu.com/p/25212301

---