信息增益

熵：

　　“形容一个系统的混乱程度”。系统的不确定性越高，熵就越大。

　　假设集合中的变量X={X1,X2,...Xn}

　　其对应在集合中的概率为P={p1,p2,...pn}

则熵表示为：

　　

 

举例：

举一个的例子：对游戏活跃用户进行分层，分为高活跃、中活跃、低活跃，游戏A按照这个方式划分，用户比例分别为20%，30%，50%。游戏B按照这种方式划分，用户比例分别为5%，5%，90%。那么游戏A对于这种划分方式的熵为：

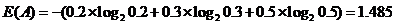
同理游戏B对于这种划分方式的熵为：

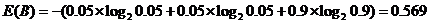
游戏A的熵比游戏B的熵大，所以游戏A的不确定性比游戏B高。用简单通俗的话来讲，游戏B要不就在上升期，要不就在衰退期，它的未来已经很确定了，所以熵低。而游戏A的未来有更多的不确定性，它的熵更高。