树，二叉树，查找算法总结

一.思维导图

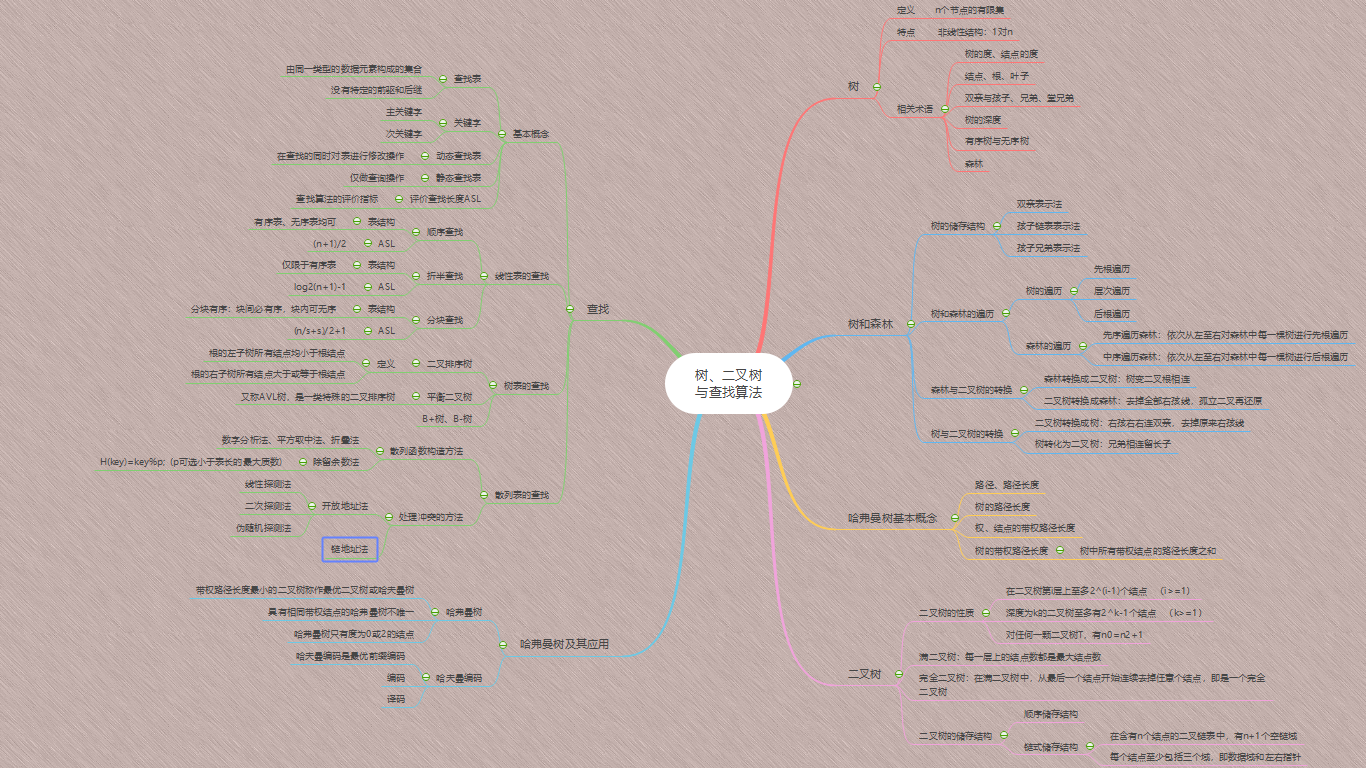
二.重要概念笔记

树的基本概念：

树(Tree)是由一个或多个结点组成的有限集合T，其中有一个特定的称为根的结点；其余结点可分为m(m≥0)个互不相交的有限集T1,T2,T3 ,…,Tm，每一个集合本身又是一棵树，且称为根的子树。

结点（Node）：树中的元素，包含数据项及若干指向其子树的分支。

结点的度（Degree）：所有结点当中，子树分支最最多的就是树的度

结点的层次：从根结点开始算起，根为第一层，

叶子（Leaf）：度为零的结点，也称端结点。

孩子（Child）：结点子树的根称为该结点的孩子结点。

双亲（Parent）：孩子结点的上层结点，称为这些结点的双亲。

兄弟（Sibling）：同一双亲的孩子。

深度（Depth)： 树中结点的最大层次数。

森林（Forest）：互不相交的树的集合。

树的储存方法：

1.双亲表示法：便于查找某结点的双亲，因为某结点的双亲是唯一的。

2.孩子表示法：便于查找孩子结点。

3.孩子兄弟表示法：便于查找孩子结点和兄弟结点，但是查找结点双亲比较困难。

二叉树：

一般树与二叉树的区别：

树的结点个数至少为1，而二叉树的结点个数可以为0；

树的结点最大度数没有限制，而二叉树结点的最大度数为2；

树的结点无左、右之分，而二叉树的结点有左、右之分。

二叉树的性质：

1.在二叉树的第K层上，最多有 2^(k-1) (K >= 1）个结点

2.深度为K的二叉树，最多有 2^k - 1 个结点（K>=1）

3.对于任何一棵二叉树，如果其叶子结点的个数为K，度为2的结点数为M,则K=M+1

4.对于一棵有 n 个结点的完全二叉树的结点按层次进行编号（如上图，从第一层到第 （log 2n 向下取整），每层从左到右），对任意结点 i （1<i<n）,有：
如果i=1，则结点i无父结点，是二叉树的根，如果i>1,则父结点为 i/2 向下取整，
如果2i>n,则结点i为叶子结点，无左子结点，否则，其左子结点为2I，
如果2i+1>n，则结点i无右子结点，否则，其右子结点是结点2i+1，

满二叉树：

一棵深度为k，且有2^k - 1个节点的树是满二叉树。

它的叶子数是： 2^(h-1)

第k层的结点数是： 2(k-1)

总结点数是： 2^k - 1

树高：h=log2(n+1)

完全二叉树：

满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

深度为k的完全二叉树，至少有2^{(k-1)个节点，至多有2}k-1个节点。

树高h=log2n + 1。

哈夫曼树：

带权路径长度最短的树，权值较大的结点离根较近。

具有相同带权结点的哈夫曼树不唯一。

哈夫曼树只有度为0与2的结点。

二叉排序树：

二叉排序树又称为二叉查找树或者二叉搜索树。

若左子树不空，则左子树上所有结点的值均小于它的根节点的值；

若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

左、右子树也分别为二叉排序树；

没有键值相等的节点。

查找算法：

基本概念：

列表：待搜索的数据集合。

关键字：要查找的那个数据。

查找，检索：一种算法过程。给出一个key值（关键字），在含有若干个结点的序列中找出它。

查找表：同一类型的数据元素的集合。

静态查找表：查询某个元素、检索指定元素的属性。

动态查找表：查找后插入、删除。

查找成功：当某个元素的key值等于给定值k，返回该元素的位置。

查找失败：所有元素的key值均不等于给定的值k，返回表示失败的标识。

顺序查找：ASL=(n+1)/2。（有序表无序表均可使用）

折半查找：ASL=log2(n+1)-1。（只适用于有序表）

分块查找：ASL=(n/s+s)/2+1。（块间需有序，块内可无序）

散列表：

散列函数构造方法：数字分析法、平方取中法、折叠法、除留余数法（最常使用）。

处理冲突的方法：线性探测法、二次探测法、伪随机探测法、拉链法。

疑难问题及解决方案：

二叉平衡树的构建这一块内容在学习之后，对二叉平衡树删除结点后重新平衡的过程感到似懂非懂，最后通过网上资料的查询，掌握了这个过程。

删除分为以下几种情况：

首先在整个二叉树中搜索要删除的结点，如果没搜索到直接返回不作处理，否则执行以下操作：

1.要删除的节点是当前根节点T。

如果左右子树都非空。在高度较大的子树中实施删除操作。

分两种情况：

(1)、左子树高度大于右子树高度，将左子树中最大的那个元素赋给当前根节点，然后删除左子树中元素值最大的那个节点。

(1)、左子树高度小于右子树高度，将右子树中最小的那个元素赋给当前根节点，然后删除右子树中元素值最小的那个节点。

如果左右子树中有一个为空，那么直接用那个非空子树或者是NULL替换当前根节点即可。

2、要删除的节点元素值小于当前根节点T值，在左子树中进行删除。

递归调用，在左子树中实施删除。

这个是需要判断当前根节点是否仍然满足平衡条件，

如果满足平衡条件，只需要更新当前根节点T的高度信息。

否则，需要进行旋转调整：

如果T的左子节点的左子树的高度大于T的左子节点的右子树的高度，进行相应的单旋转。否则进行双旋转。

3、要删除的节点元素值大于当前根节点T值，在右子树中进行删除。