[2020 CCPC - Mianyang Site] B. Building Blocks(动态规划)

[2020 CCPC - Mianyang Site] B. Building Blocks(动态规划)

题目链接：

https://codeforces.com/gym/102822/problem/B

题意：

给定一个\(n*m\)的方框，告诉了你其在左前面投影时长度为\(n+m\)的高度\(\mathit h\)，以及\(\mathit k\)个位置是固定的高度。

现在问你有多少种方案可以满足上述要求。

思路：

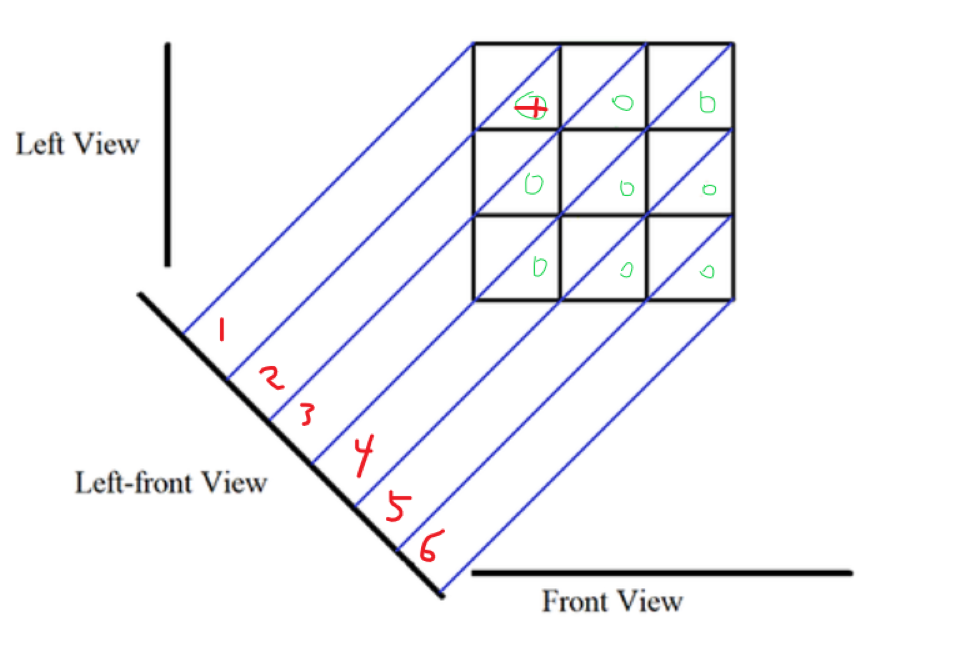
我们对斜面投影，考虑用数组存下上图没被确定的绿色部分的个数\(flex_i\)，

我们容易发现，一个方格会被两个投影高度所限制，第\((x,y)\)个方格分别是被\((x+y-1),(x+y)\)这两个投影限制。

那么我们考虑设动态规划状态：

\(dp[i][0/1]\) 代表满足\(x+y<i\)的点\((x,y)\)都符合条件且达到投影所要求的高度，而\(x+y=i\)的方格们的高度在不违反限制的情况下是否达到要求的方案数（0代表没打到，即当前\(x+y=i\)的点们最高的部分小于投影高度。反而反之。）

转移就是这几种情况：

从\(dp[i-1][0]\)转移到\(dp[i][0]\)，需要\(h[i]>h[i-1]\)，且投影的第\(\mathit i\) 行最高高度取\(h[i-1]\)。

从\(dp[i-1][0]\)转移到\(dp[i][1]\)，需要\(h[i]=h[i-1]\)，且投影的第\(\mathit i\) 行最高高度取\(h[i-1]\)。

从\(dp[i-1][1]\)转移到\(dp[i][0]\)，需要投影的第\(\mathit i\) 行最高高度不超过\(min(h[i-1],h[i]-1)\)。

从\(dp[i-1][1]\)转移到\(dp[i][1]\)，需要\(h[i]<=h[i-1]\)，且投影的第\(\mathit i\) 行最高高度取\(h[i]\)。

每条斜线的最高高度max分成两部分:

已知的高度的\(peak_i\)

剩下待确定的\(flex_i\)个积木

对于任意一个\(\mathit i\)，如果\(peak_i>h_i\)，肯定是无解的。

对于任意一个\(\mathit i\)，如果\(peak_i=h_i\)，那么\(dp[i][0]=0\)，转移从\(dp[i-1][0]\)来的话，需要\(flex_i\)中有取到\(h[i-1]\)高的。转移从\(dp[i-1][1]\)来的话，剩下\(flex_i\)中不超过限制任取即可。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7ll;
int n, m, k;
const int maxn = 2e5 + 10;
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}

ll F(ll n, ll k)// k个数,至少有一个是n
{
    return (powmod(n, k, mod) - powmod(n - 1, k, mod) + mod) % mod;
}
ll G(ll n, ll k)// k个数,在[1,n]中随意取值
{
    return powmod(n, k, mod);
}

ll dp[maxn][2];
int flex[maxn];
int h[maxn];
int peak[maxn];
int main()
{
    int t;
    scanf("%d", &t);
    for (int icase = 1; icase <= t; ++icase) {
        scanf("%d %d %d", &n, &m, &k);
        for (int i = 1; i <= n + m; ++i) {
            scanf("%d", &h[i]);
        }
        for (int i = 0; i <= n + m + 1; ++i) {
            peak[i] = flex[i] = dp[i][0] = dp[i][1] = 0;
        }
        int len = n + m;
        for (int i = 2; i <= n + m; ++i)  {
            flex[i] = min(min(i - 1, len - i + 1), min(n, m));
        }
        bool flag = 0;
        for (int i = 1; i <= k; i++) {
            int x, y, w;
            scanf("%d %d %d", &x, &y, &w);
            flex[x + y]--;
            peak[x + y] = max(peak[x + y], w);
            peak[x + y - 1] = max(peak[x + y - 1], w);
            if (w > h[x + y] || w > h[x + y - 1]) {
                flag = 1;
            }
        }
        printf("Case #%d: ", icase);
        if (flag) {
            printf("0\n");
            continue;
        }
        if (peak[1] == h[1]) {
            dp[1][1] = 1;
        } else {
            dp[1][0] = 1;
        }
        for (int i = 2; i <= len; i++)  {
            ll pre = h[i - 1];
            ll now = h[i];
            if (peak[i] == h[i]) {
                dp[i][0] = 0ll;
                if (pre <= now) {
                    dp[i][1] += dp[i - 1][0] * F(pre, flex[i]) % mod;
                    dp[i][1] %= mod;
                }
                dp[i][1] += dp[i - 1][1] * G(min(now, pre), flex[i]) % mod;
                dp[i][1] %= mod;
            } else {
                if (pre == now) {
                    dp[i][1] += dp[i - 1][0] * F(pre, flex[i]) % mod;
                    dp[i][1] %= mod;
                }
                if (pre >= now) {
                    dp[i][1] += dp[i - 1][1] * F(now, flex[i]) % mod;
                    dp[i][1] %= mod;
                } else {
                    dp[i][0] += dp[i - 1][0] * F(pre, flex[i]) % mod;
                    dp[i][0] %= mod;
                }
                dp[i][0] += dp[i - 1][1] * G(min(now - 1, pre), flex[i]) % mod;
                dp[i][0] %= mod;
            }
        }
        printf("%lld\n", dp[len][1] );
    }
    return 0;
}