[Codeforces Round #125 (Div. 2)] B. Special Olympics（圆的关系问题）

[Codeforces Round #125 (Div. 2)] B. Special Olympics

题目链接：https://codeforces.com/contest/199/problem/B

题面：

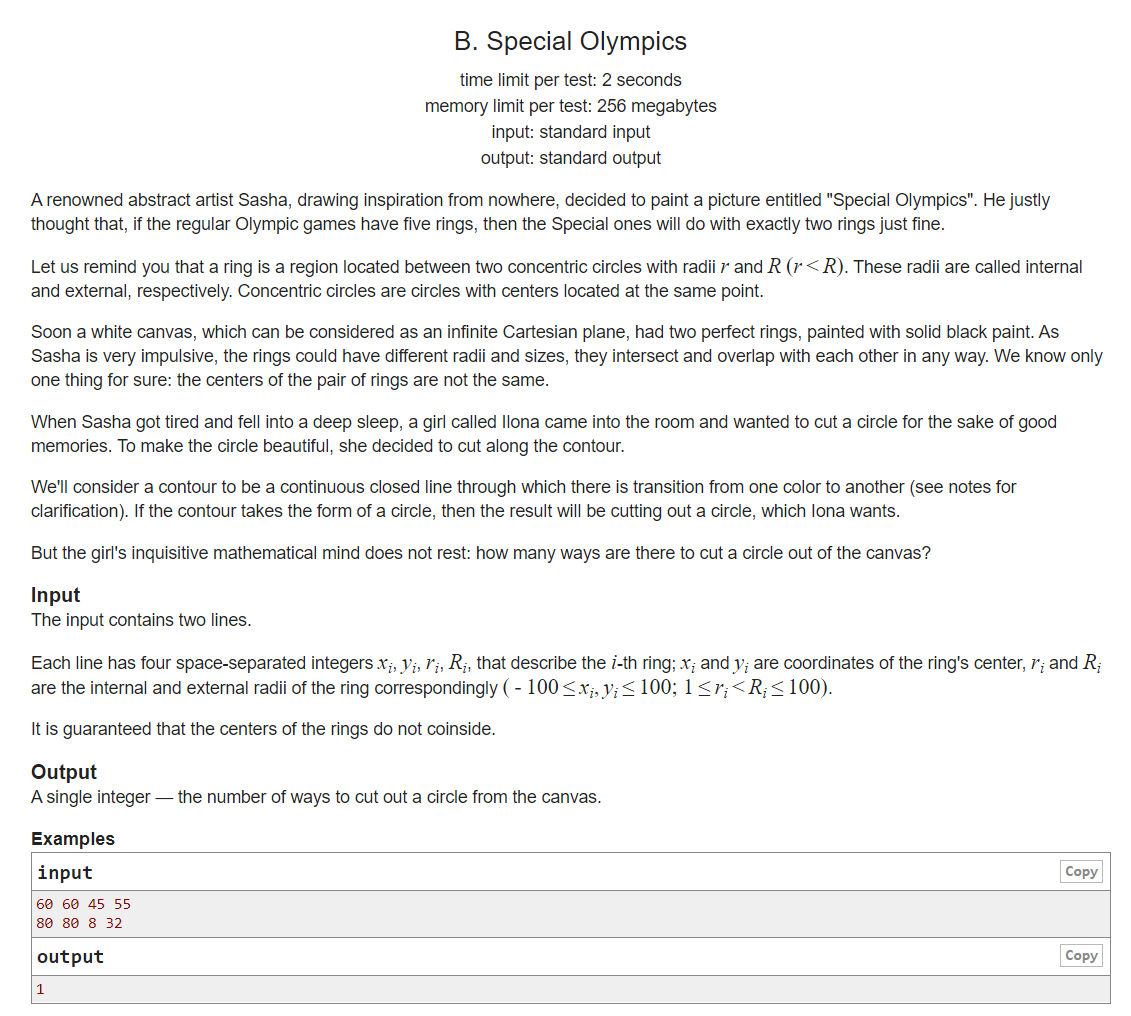
题意：

在一个无限大的白色二维平面，有两个圆环，圆环部分被涂为黑色。

一个轮廓是通过连续封闭的线从一个色彩过渡到另一个色彩。

现在问有多少个轮廓是圆形？

思路：

注意本题中内切考虑为内含，外切考虑为外离，因为一个点不影响轮廓线。

考虑对每一个圆环上的圆去判断是否有完整的轮廓。

如有以下中任意一点，则无完整的轮廓：

• 与另一个圆环上的某个圆交点个数大于2.

• 该圆在另一个圆环中，有两种情况（绿色均在橙色圆环内）：

  该圆内含另一个圆环的内圆，又被另一个圆环的外圆内含。

  

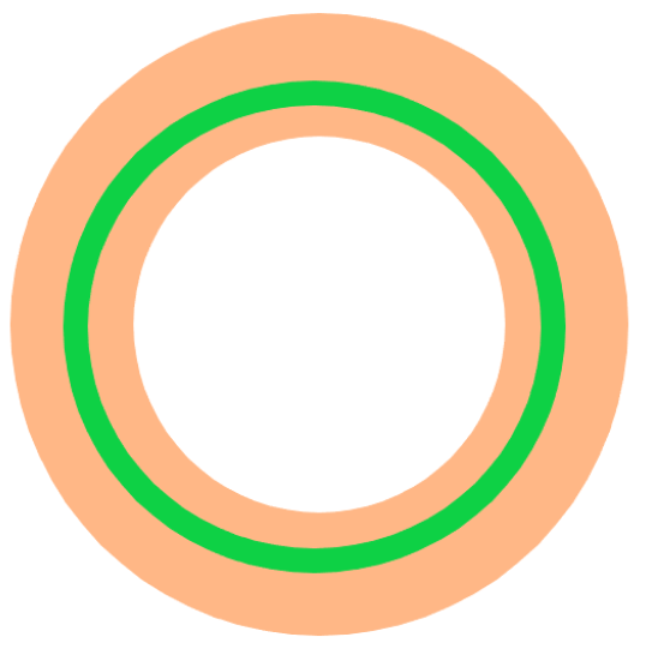
  该圆外离另一个圆环的内圆，又被另一个圆环的外圆内含。

  

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <bits/stdc++.h>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define chu(x)  if(DEBUG_Switch) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
ll poww(ll a, ll b) { if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a ;} a = a * a ; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline long long readll() {long long tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') { fh = -1; } c = getchar();} while (c >= '0' && c <= '9') { tmp = tmp * 10 + c - 48, c = getchar(); } return tmp * fh;}
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') { fh = -1; } c = getchar();} while (c >= '0' && c <= '9') { tmp = tmp * 10 + c - 48, c = getchar(); } return tmp * fh;}
void pvarr_int(int *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%d%c", arr[i], i == n ? '\n' : ' ');}}
void pvarr_LL(ll *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%lld%c", arr[i], i == n ? '\n' : ' ');}}
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
#define DEBUG_Switch 0
struct Point {
    double x, y;
    Point()
    {
        x = y = 0;
    }
    Point(double a, double b)
    {
        x = a, y = b;
    }
    inline Point operator-(const Point &b)const
    {
        return Point(x - b.x, y - b.y);
    }
    inline Point operator+(const Point &b)const
    {
        return Point(x + b.x, y + b.y);
    }
    inline double dot(const Point &b)const
    {
        return x * b.x + y * b.y;
    }
    inline double cross(const Point &b, const Point &c)const
    {
        return (b.x - x) * (c.y - y) - (c.x - x) * (b.y - y);
    }
};
int dcmp(double x)
{
    if (x > eps) { return 1; }
    return x < -eps ? -1 : 0;
}

struct Circle {
    Point c;
    double r;
    Circle(Point c = Point(0, 0), double r = 0) : c(c), r(r) {}
    Point point(double a) { return Point(c.x + cos(a) * r, c.y + sin(a) * r); }
};
bool operator ==(const Point &a, const Point &b)
{
    return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}
double angle(Point v) { return atan2(v.y, v.x); }
double dot(Point A, Point B) { return A.x * B.x + A.y * B.y;}
double det(Point A, Point B) { return A.x * B.y - A.y * B.x;}
double Length(Point A) { return sqrt(dot(A, A));}

int getCircleCircleIntersection(Circle C1, Circle C2)
{
    double d = Length(C1.c - C2.c);
    if (dcmp(d) == 0) {
        if (dcmp(C1.r - C2.r) == 0) { return -1; } //两圆重合
        return 0;
    }
    if (dcmp(fabs(C1.r - C2.r) - d) >= 0) {
        if (C1.r > C2.r) {
            return 3;
        } else {
            return 4;
        }
    }       //内含
    // r1+r1>d
    if (dcmp(d - C1.r - C2.r) >= 0) { return 0; } //外离
    double a = angle(C2.c - C1.c); //向量C1C2的极角
    double da = acos((C1.r * C1.r + d * d - C2.r * C2.r) / (2 * C1.r * d));
    //C1C2到C1P1的角
    Point p1 = C1.point(a - da), p2 = C1.point(a + da);
    if (p1 == p2) { return 1; }
    return 2;
}
Circle c1, c2, c3, c4;
int main()
{
#if DEBUG_Switch
    freopen("D:\\code\\input.txt", "r", stdin);
#endif
    //freopen("D:\\code\\output.txt","w",stdout);
    c1.c.x = readint();
    c1.c.y = readint();
    c2.c = c1.c;
    c1.r = readint();
    c2.r = readint();
    c3.c.x = readint();
    c3.c.y = readint();
    c4.c = c3.c;
    c3.r = readint();
    c4.r = readint();
    int ans = 0;
    int res13 = getCircleCircleIntersection(c1, c3);
    int res14 = getCircleCircleIntersection(c1, c4);
    int res23 = getCircleCircleIntersection(c2, c3);
    int res24 = getCircleCircleIntersection(c2, c4);
//    cout << res13 << " " << res14 << " " << res23 << " " << res24 << endl;
    if (res13 != 2 && res14 != 2 && res13 + res14 != 7 && !(res13 == 0 && res14 > 2) ) {
        ans++;
    }
    if (res23 != 2 && res24 != 2 && res23 + res24 != 7 && !(res23 == 0 && res24 > 2)) {
        ans++;
    }
    if (res13 != 2 && res23 != 2 && res13 + res23 != 7 && !(res13 == 0 && res23 > 2) ) {
        ans++;
    }
    if (res14 != 2 && res24 != 2 && res14 + res24 != 7 && !(res14 == 0 && res24 > 2)  ) {
        ans++;
    }
    printf("%d\n", ans );
    return 0;
}
/*

0 0 50 70
1 0 60 80

 */