数学推导- 圆上任取3个点构成三角形

数学推导- 圆上任取3个点构成三角形

题意：

在圆上取N个点，以至将圆弧分成N等份，求任取3个点能构成多少个锐角三角形

思路：

求所有不同锐角三角形的个数，只需要求出所有三角形的个数\(C(n,3)\)，

然后减去钝角和直角三角形的个数。下面考虑计算：

• 当\(\mathit n\)为偶数：

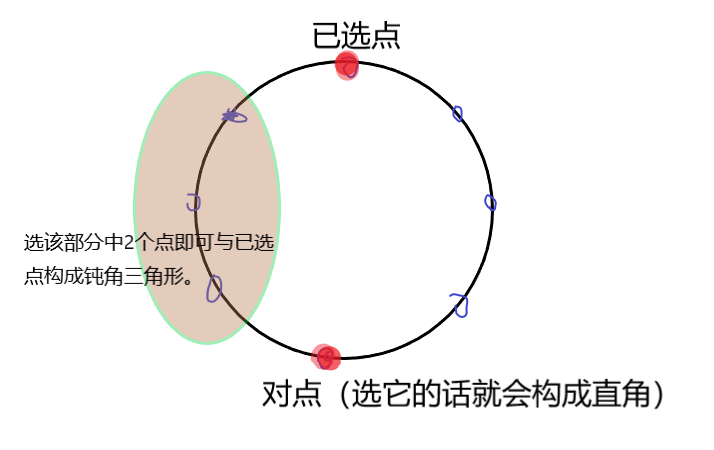
  直角三角形个数：\(n*(n-2)\)，即圆上\(\mathit n\)个点任意选择一个点，这其经过直径的对点一定要选，剩下的\(n-2\)个点可以任意选。

  钝角三角形个数：\(n*C(\frac{n-2}{2},2)\)，即圆上\(\mathit n\)个点任意选择一个点，则剩余两个点一定要选该点与经过直径的对点之间的一侧的，为了不重复计数，我们只考虑选择划分为的两侧中的一侧，即\(\frac{n-2}{2}\)中选择任意两个。
  

• 当\(\mathit n\)为奇数：

  直角三角形个数：0

  钝角三角形个数：\(n*C(\frac{n}{2},2)\)，即圆上\(\mathit n\)个点任意选择一个点，则剩余两个点一定要选该点与经过直径的对点之间的一侧的，为了不重复计数，我们只考虑选择划分为的两侧中的一侧，即\(\frac{n}{2}\)中选择任意两个。

通过化简和等价变换可以得到奇偶的情况是同一个公式，即：

最终可以得出答案为

\[C(n,3)-C(n,1)*C(n/2,2); \]

代码：

	long long n;
    while(scanf("%lld",&n)!=EOF)
    {
        printf("%lld\n",((n-1)*(n-2))*n/3/2-((n/2-1)*(n/2)/2*n));
    }

一点拓展：

• 圆上任取三个点组成锐角三角形的概率为\(\frac{1}{4}\)
• 圆上任取三个点组成钝角三角形的概率为\(\frac{3}{4}\)
• 圆上任取三个点组成直角三角形的概率为\(\text 0\)

证明可以参考：https://zhuanlan.zhihu.com/p/69530841