HDU-6767 New Equipments （最小费用最大流，费用流）

HDU-6767 New Equipments （最小费用最大流，费用流）

Problem Description

Little Q's factory recently purchased m pieces of new equipment, labeled by 1,2,…,m.

There are n workers in the factory, labeled by 1,2,…,n. Each worker can be assigned to no more than one piece of equipment, and no piece of equipment can be assigned to multiple workers. If Little Q assigns the i-th worker to the j-th piece of equipment, he will need to pay ai×j2+bi×j+ci dollars.

Now please for every k (1≤k≤n) find k pairs of workers and pieces of equipment, then assign workers to these pieces of equipment, such that the total cost for these k workers is minimized.

题意：

给定\(\mathit n\)个开口向上的一元二次函数（而且保证函数的最小值大于等于\(\text 0\)），让你输出\(\mathit n\)个结果，

第\(\mathit i\)个结果代表从\([1,m]\)这个区间中，选择\(\mathit i\)个整数点和一个函数，并把整数点和函数们匹配一下，每一个函数只能与一个点匹配，每一个点只能和一个函数匹配。结果为所有组合中，最小的函数值总和。

其中\(n\in[1,50],m\in[1,10^8]\)。

思路：

虽然正整数给的很多，但是每个函数只会在最小值点左右若干个点取值。

我们对每一个函数，在其最小值周围取\(min(m,100)\)个点（尽量在最值附**分左右的取即可保证最小。）

这样一共有\(100*n\)个数，\(\mathit n\)个函数。将其都设成图中的节点，并建立一个超级源点，汇点\(S,T\)。

然后以以下方式建立一个流量网络：

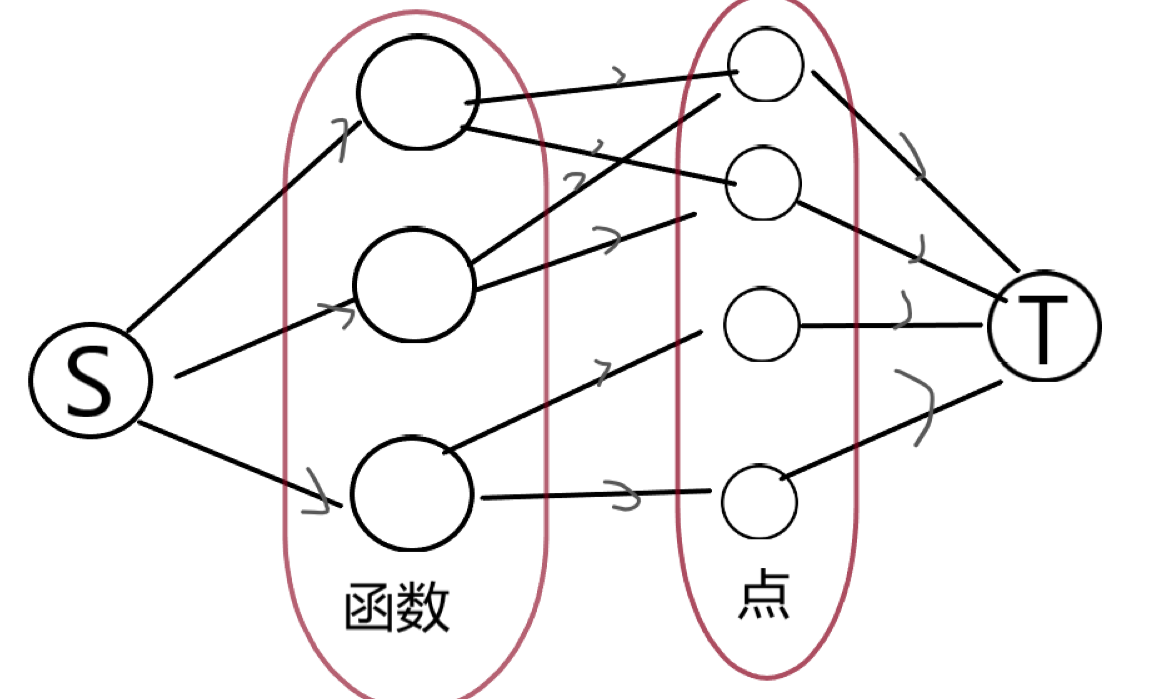
图仅为抽象图，不代表具体样例。

每个边的流量和单位流量费用的设置：

\(S->\)每个函数，流量为1，费用为0.

每个函数到它取值前\(min(100,m)\)的点建边：流量为1，费用为点带入到函数的函数值。

每一个点和汇点建边：流量为1，费用为0.

那么根据最小费用最流量算法原理和增广路定理，

第一次求最短路的增光路的费用即位\(i=1\)的答案，

前两次求最短路的增光路的费用即位\(i=2\)的答案，

...

所以一次最小费用最流量算法即可解决本题。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <bits/stdc++.h>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define chu(x)  if(DEBUG_Switch) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
ll poww(ll a, ll b) { if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a ;} a = a * a ; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline long long readll() {long long tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
void pvarr_int(int *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%d%c", arr[i], i == n ? '\n' : ' ');}}
void pvarr_LL(ll *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%lld%c", arr[i], i == n ? '\n' : ' ');}}
const int maxn = 2600;
const ll inf = 1e18;
/*** TEMPLATE CODE * * STARTS HERE ***/
#define DEBUG_Switch 0
const int MAX_N = 6500;
const int MAX_M = MAX_N * 10;

struct edge {
    int v; ll c, w; int  next; // v 表示边的另一个顶点，c 表示当前剩余容量，w 表示单位流量费用
};
struct MCMF
{
    edge e[MAX_M];
    int p[MAX_N], s, t, eid;  // s 表示源点，t 表示汇点，需要在进行 costflow 之前设置完毕
    void init() {
        memset(p, -1, sizeof(p));
        eid = 0;
    }
    void insert(int u, int v, ll c, ll w) {
        e[eid].v = v;
        e[eid].c = c;
        e[eid].w = w;
        e[eid].next = p[u];
        p[u] = eid++;
    }
    void addedge(int u, int v, ll c, ll w) {
        insert(u, v, c, w);
        insert(v, u, 0, -w);
    }
    bool vis[MAX_N];
    ll d[MAX_N];  // 如果到顶点 i 的距离是 inf，则说明不存在源点到 i 的最短路
    // int - memset-> 0x3f  ll - memset-> 0x7f
    int pre[MAX_N];  // 最短路中连向当前顶点的边的编号
    bool dijk() {  // 以源点 s 为起点计算单源最短路，如果不存在从 s 到 t 的路径则返回 false，否则返回 true
        memset(d, 0x7f, sizeof(d));
        memset(pre, -1, sizeof(pre));
        d[s] = 0;
        priority_queue<pll, vector<pll>, greater<pll> > q;
        q.push(mp(0, s));
        while (!q.empty())
        {
            pll temp = q.top();
            q.pop();
            int u = temp.se;
            if (u == t || d[u] < temp.fi)
                continue;
            for (int i = p[u]; i != -1; i = e[i].next) {
                if (e[i].c) {
                    int v = e[i].v;
                    if (d[u] + e[i].w < d[v])
                    {
                        d[v] = d[u] + e[i].w;
                        pre[v] = i;
                        q.push(mp(d[v], v));
                    }
                }
            }
        }
        return pre[t] != -1;
    }
    void min_cost_flow() {  // 计算最小费用最大流
        bool flag = 0;
        ll ret = 0;  // 累加和
        while (dijk()) {
            if (flag)
            {
                printf(" ");
            }
            ll flow = inf;
            for (int i = t; i != s; i = e[pre[i] ^ 1].v) {
                flow = min(e[pre[i]].c, flow);  // 计算当前增广路上的最小流量
            }
            for (int i = t; i != s; i = e[pre[i] ^ 1].v) {
                e[pre[i]].c -= flow;     //容量是一定要跟着变化的，毕竟要继续循环使用dijk来更新下一条“能走的（看容量）”最短路。
                e[pre[i] ^ 1].c += flow;
                ret += e[pre[i]].w * flow;
            }
            printf("%lld", ret );
            flag = 1;
        }
        printf("\n");
    }
} gao;
int n, m;
ll a[maxn];
ll b[maxn];
ll c[maxn];
map<int, int> vis;
int main()
{
#if DEBUG_Switch
    freopen("C:\\code\\input.txt", "r", stdin);
#endif
    //freopen("C:\\code\\output.txt","w",stdout);
    int ww;
    ww = readint();
    while (ww--)
    {
        vis.clear();
        n = readint();
        m = readint();
        repd(i, 1, n)
        {
            a[i] = readll();
            b[i] = readll();
            c[i] = readll();
        }
        gao.init();
        gao.s = 0;
        gao.t = 1;
        int id = n + 1;
        repd(i, 1, n)
        {
            int mid = (-b[i] / (a[i] * 2));
            gao.addedge(gao.s, i + 1, 1, 0);
            for (int j = max(1, mid - 55), cnt = 0; cnt <= 101 && j <= m; cnt++, j++)
            {
                int x;
                if (vis.count(j) == 0)
                {
                    vis[j] = ++id;
                    gao.addedge(id, gao.t, 1, 0);
                }
                x = vis[j];
                gao.addedge(i + 1, x, 1, a[i]*j * j + b[i]*j + c[i]);
            }
        }
        gao.min_cost_flow();
    }

    return 0;
}