洛谷P3400 仓鼠窝（单调栈）

P3400 仓鼠窝

题目描述

萌萌哒的Created equal是一只小仓鼠，小仓鼠自然有仓鼠窝啦。

仓鼠窝是一个由nm个格子组成的行数为n、列数为m的矩阵。小仓鼠现在想要知道，这个矩阵中有多少个子矩阵！（实际上就是有多少个子长方形嘛。）比如说有一个23的矩阵，那么11的子矩阵有6个，12的子矩阵有4个，13的子矩阵有2个，21的子矩阵有3个，22的子矩阵有2个，23的子矩阵有1个，所以子矩阵共有6+4+2+3+2+1=18个。

可是仓鼠窝中有的格子被破坏了。现在小仓鼠想要知道，有多少个内部不含被破坏的格子的子矩阵！

题意：

给定一个\(n*m\)的01矩阵，让你计算有多少个子矩阵只包含数字1？

思路：

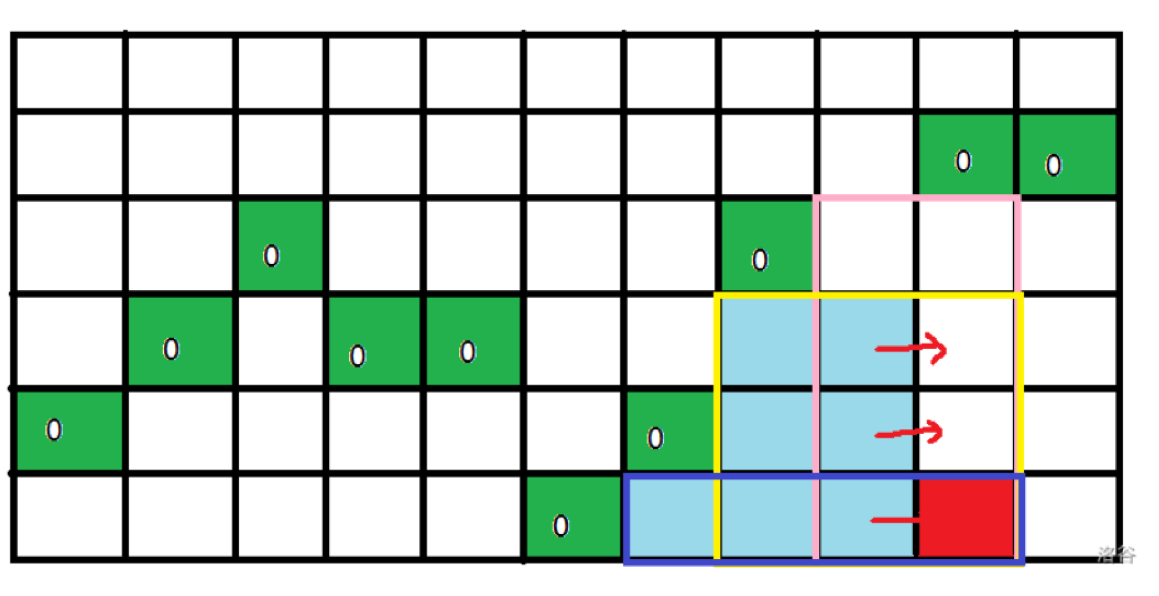
观察上图，

考虑计算每一个节点做多少个子矩阵的右下角，加起来就是答案。

我们用数组\(height_j\)维护第\(\mathit j\)列最低的数字0的高度。

用\(sum_j\)代表当前行的第\(\mathit j\)列的答案。

对于上图中的这个红点，这些各色矩形内的点就是可取的答案，矩形的大小因为0的存在受到限制。

容易发现，这些真正挡住矩形向外扩张的的‘0’从左往右是单调递增的，而比这些0更靠左还更高的‘0’显然是毫无用处的。

然后我们对每一行进行分别处理，

用单调栈维护从左往右是单调递增的数字0的高度，

对于图中红色因为本列的0一定不低于单调栈中左边一列的0，所以之前左边一列的答案（图中浅蓝色）可以直接继承，同时还要加上最新一个形成的矩形(粉色矩形上端)贡献的答案。

所以当前第\(\mathit j\)列的\(sum_j=sum_{st[top-1]}+(j - st[head - 1]) * (i - height[j])\)。

然后计入总答案\(ans\)即可。

记得本题目要开long long 存答案。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#include <sstream>
#include <bitset>
#include <unordered_map>
// #include <bits/stdc++.h>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define chu(x)  if(DEBUG_Switch) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
ll poww(ll a, ll b) { if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a ;} a = a * a ; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline long long readll() {long long tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
void pvarr_int(int *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%d%c", arr[i], i == n ? '\n' : ' ');}}
void pvarr_LL(ll *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%lld%c", arr[i], i == n ? '\n' : ' ');}}
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
#define DEBUG_Switch 0
int n, m;
int a[3003][3003];
int head, st[3003];
int height[3003];
ll ans = 0ll;
ll sum[3003];
int main()
{
#if DEBUG_Switch
    freopen("C:\\code\\input.txt", "r", stdin);
#endif
    //freopen("C:\\code\\output.txt","r",stdin);
    n = readint();
    m = readint();
    repd(i, 1, n)
    {
        repd(j, 1, m)
        {
            a[i][j] = readint();
        }
    }
    repd(i, 1, n)
    {
        repd(j, 1, m)
        {
            if (a[i][j] == 0)
            {
                height[j] = i;
            }
            while (head > 0 && height[st[head]] <= height[j])
            {
                head--;
            }
            st[++head] = j;
            sum[j] = sum[st[head - 1]] + 1ll * (j - st[head - 1]) * (i - height[j]);
            ans += sum[j];
        }
        head=0;
    }
    printf("%lld\n", ans );
    return 0;
}