[Codeforces Round #636 (Div. 3)] E. Weights Distributing （BFS+最短路+贪心）

[Codeforces Round #636 (Div. 3)] E. Weights Distributing （BFS+最短路+贪心）

E. Weights Distributing

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected unweighted graph consisting of nn vertices and mm edges (which represents the map of Bertown) and the array of prices pp of length mm. It is guaranteed that there is a path between each pair of vertices (districts).

Mike has planned a trip from the vertex (district) aa to the vertex (district) bb and then from the vertex (district) bb to the vertex (district) cc. He can visit the same district twice or more. But there is one issue: authorities of the city want to set a price for using the road so if someone goes along the road then he should pay the price corresponding to this road (he pays each time he goes along the road). The list of prices that will be used pp is ready and they just want to distribute it between all roads in the town in such a way that each price from the array corresponds to exactly one road.

You are a good friend of Mike (and suddenly a mayor of Bertown) and want to help him to make his trip as cheap as possible. So, your task is to distribute prices between roads in such a way that if Mike chooses the optimal path then the price of the trip is the minimum possible. Note that you cannot rearrange prices after the start of the trip.

You have to answer tt independent test cases.

Input

The first line of the input contains one integer tt (1≤t≤1041≤t≤104) — the number of test cases. Then tt test cases follow.

The first line of the test case contains five integers n,m,a,bn,m,a,b and cc (2≤n≤2⋅1052≤n≤2⋅105, n−1≤m≤min(n(n−1)2,2⋅105)n−1≤m≤min(n(n−1)2,2⋅105), 1≤a,b,c≤n1≤a,b,c≤n) — the number of vertices, the number of edges and districts in Mike's trip.

The second line of the test case contains mm integers p1,p2,…,pmp1,p2,…,pm (1≤pi≤1091≤pi≤109), where pipi is the ii-th price from the array.

The following mm lines of the test case denote edges: edge ii is represented by a pair of integers vivi, uiui (1≤vi,ui≤n1≤vi,ui≤n, ui≠viui≠vi), which are the indices of vertices connected by the edge. There are no loops or multiple edges in the given graph, i. e. for each pair (vi,uivi,ui) there are no other pairs (vi,uivi,ui) or (ui,viui,vi) in the array of edges, and for each pair (vi,ui)(vi,ui) the condition vi≠uivi≠ui is satisfied. It is guaranteed that the given graph is connected.

It is guaranteed that the sum of nn (as well as the sum of mm) does not exceed 2⋅1052⋅105 (∑n≤2⋅105∑n≤2⋅105, ∑m≤2⋅105∑m≤2⋅105).

Output

For each test case, print the answer — the minimum possible price of Mike's trip if you distribute prices between edges optimally.

Example

input

Copy

2
4 3 2 3 4
1 2 3
1 2
1 3
1 4
7 9 1 5 7
2 10 4 8 5 6 7 3 3
1 2
1 3
1 4
3 2
3 5
4 2
5 6
1 7
6 7

output

Copy

7
12

Note

One of the possible solution to the first test case of the example:

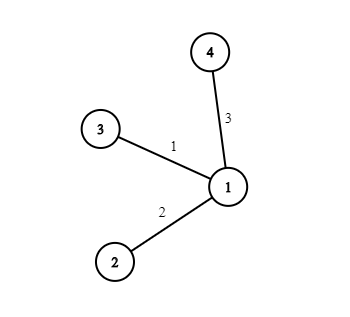
One of the possible solution to the second test case of the example:

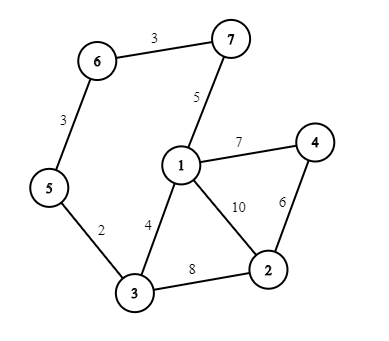
题意：

给定一个含有\(\mathit n\)个节点\(\mathit m\)条边的无向无环图，三个节点\(a,b,c\)

以及一个大小为\(\mathit m\)的数组\(\mathit p\)，现在的任务是从数组\(\mathit p\)中选出一个\(p_j\)作为第\(\mathit i\)条边的边权，且每一个\(p_j\)只可以被使用一次，要求使得\((a->b->c)\)的最短路径值最小。

思路：

所有的路径情况可以被分类成两种：

1️⃣：

\((a->b),(b->c)\)两个径直的路径，有且仅有一个连接点\(\mathit b\)，样例二就是这一类。

2️⃣：

存在一个非\(\mathit b\)的节点\(\mathit x\)，路径为：\((a->x),(x->b),(b->x),(x->c)\)，样例一就属于这一类。

仔细思考的话可以发现，两种情况可以都归纳为情况2️⃣，

因为\(a,b,c\)都是确定的，那么我们不枚举节点\(\mathit x\)，

在枚举之前，我们通过\(\text 3\)次\(bfs\)算法分别求出以\(a,b,c\)为源点的到达地\(\mathit i\)个节点的最短距离（需要经历多少个边）。

因为\((b->x)\)这个路径需要被走两次，那么我们肯定优先把边权小的边放在路径\((b->x)\)上。

只需要将数组\(\mathit p\)排序后做个sum和即可\(O(m*log_2(m)+n)\)的时间复杂度内解决该问题。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#include <sstream>
#include <bitset>
#include <unordered_map>
// #include <bits/stdc++.h>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define chu(x)  if(DEBUG_Switch) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
ll poww(ll a, ll b) { if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a ;} a = a * a ; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline long long readll() {long long tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
void pvarr_int(int *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%d%c", arr[i], i == n ? '\n' : ' ');}}
void pvarr_LL(ll *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%lld%c", arr[i], i == n ? '\n' : ' ');}}
const int maxn = 200010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
#define DEBUG_Switch 0
int n, m, a, b, c;
int dis1[maxn];
int dis2[maxn];
int dis3[maxn];
std::vector<int> v[maxn];
int p[maxn];
ll sum[maxn];
queue<int> q;
void bfs(int strat, int * dis )
{
    repd(i, 1, n)
    {
        dis[i] = inf;
    }
    dis[strat] = 0;
    q.push(strat);
    int temp;
    while (!q.empty())
    {
        temp = q.front();
        q.pop();
        for (auto &y : v[temp])
        {
            if (dis[y] == inf)
            {
                dis[y] = dis[temp] + 1;
                q.push(y);
            }
        }
    }
}
int main()
{
#if DEBUG_Switch
    freopen("C:\\code\\input.txt", "r", stdin);
#endif
    //freopen("C:\\code\\output.txt","r",stdin);
    int t;
    t = readint();
    while (t--)
    {
        n = readint();
        m = readint();
        a = readint();
        b = readint();
        c = readint();
        repd(i, 1, m)
        {
            p[i] = readint();
        }
        sort(p + 1, p + 1 + m);
        repd(i, 1, m)
        {
            sum[i] = sum[i - 1] + p[i];
        }
        repd(i, 1, m)
        {
            int x, y;
            x = readint();
            y = readint();
            v[x].pb(y);
            v[y].pb(x);
        }
        bfs(a, dis1);
        bfs(b, dis2);
        bfs(c, dis3);
        ll ans = 1e18;
        repd(i, 1, n)
        {
            int num1 = dis1[i];
            int num2 = dis2[i];
            int num3 = dis3[i];
            if (num2 + num1 + num3 > m)
                continue;
            ll temp = 2ll * sum[num2] + (sum[num1 + num3 + num2] - sum[num2]);
            ans = min(temp, ans);
        }
        printf("%lld\n", ans );
        repd(i, 1, n)
        {
            v[i].clear();
        }
    }

    return 0;
}