[Codeforces Round #624 (Div. 3)] -E. Construct the Binary Tree (构造二叉树)
[Codeforces Round #624 (Div. 3)] -E. Construct the Binary Tree (构造二叉树)
E. Construct the Binary Tree
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given two integers nn and dd. You need to construct a rooted binary tree consisting of nn vertices with a root at the vertex 11 and the sum of depths of all vertices equals to dd.
A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. A parent of a vertex vv is the last different from vv vertex on the path from the root to the vertex vv. The depth of the vertex vv is the length of the path from the root to the vertex vv. Children of vertex vv are all vertices for which vv is the parent. The binary tree is such a tree that no vertex has more than 22 children.
You have to answer tt independent test cases.
Input
The first line of the input contains one integer tt (1≤t≤10001≤t≤1000) — the number of test cases.
The only line of each test case contains two integers nn and dd (2≤n,d≤50002≤n,d≤5000) — the number of vertices in the tree and the required sum of depths of all vertices.
It is guaranteed that the sum of nn and the sum of dd both does not exceed 50005000 (∑n≤5000,∑d≤5000∑n≤5000,∑d≤5000).
Output
For each test case, print the answer.
If it is impossible to construct such a tree, print "NO" (without quotes) in the first line. Otherwise, print "{YES}" in the first line. Then print n−1n−1 integers p2,p3,…,pnp2,p3,…,pn in the second line, where pipi is the parent of the vertex ii. Note that the sequence of parents you print should describe some binary tree.
Example
input
Copy
3
5 7
10 19
10 18
output
Copy
YES
1 2 1 3
YES
1 2 3 3 9 9 2 1 6
NO
Note
Pictures corresponding to the first and the second test cases of the example:
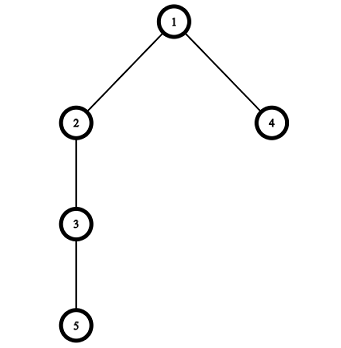
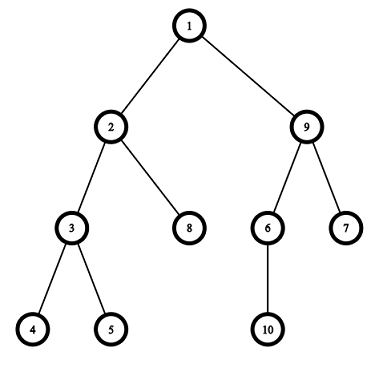
题意:
有\(\mathit t\)组数据,每一组数据包含2个整数\(n,d\),让你构造出一个以节点1为根的二叉树使其每个节点的深度的sum和为d。
思路:
我们定义每个节点的深度的sum和为\(now\)
我们首先找出\(now\)的上下限,分析可以得知:
当树为一个1节点为端点的链时\(now\)值最大,为\(now_{max}\)。
当树为一个1节点为根的完全二叉树时\(now\)值最小,为\(now_{min}\)。
如果\(\mathit d\)不在区间\([now_{min},now_{max}]\)中直接输出NO,
否则进行构造树:
先构造一个1节点为端点的长度为n的链,同时保存树的信息:\(son[i][0]\)代表第i个节点的左儿子,\(son[i][1]\)代表第i个节点的右儿子。
并且dfs去维护以下信息:
\(vector<int> v[i]\)存储深度为\(\mathit i\)的节点。(1节点的深度为0)
如果当前的\(now>d\)考虑将一个节点\(id\)(从初始深度最大的n开始)接入一个\(depth[j]=dep[id] - 2\)的节点\(\mathit j\)
,这样可以使now值减去1,如果没有满足条件的\(\mathit j\),说明深度从\(0->depth[j]\)的二叉树已满无法插入节点$\mathit i \(,则\)id$减去1,重复此过程,直到使now减去1。
这样我们可以构造出\([now_{min},now_{max}]\)中的所有值。
因为\(2 \le n, d \le 5000\),我们算法的每一组时间复杂度为\(O(n*d)\),所以可以顺利的通过题目。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#include <sstream>
#include <bitset>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline long long readll() {long long tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int n, d;
int son[maxn][2];
int dep[maxn];
int fa[maxn];
int we;
std::vector<int> v[maxn];
int dfs(int x, int step, int pre)
{
v[step].pb(x);
fa[x] = pre;
int res = step;
dep[x] = step;
if (son[x][0])
{
res += dfs(son[x][0], step + 1, x);
}
if (son[x][1])
{
res += dfs(son[x][1], step + 1, x);
}
if (pre == 0)
we = res;
return res;
}
void init()
{
repd(i, 0, n + 2)
{
son[i][0] = son[i][1] = 0;
dep[i] = 0;
fa[i] = 0;
}
}
int main()
{
//freopen("D:\\code\\text\\input.txt","r",stdin);
//freopen("D:\\code\\text\\output.txt","w",stdout);
int t;
t = readint();
while (t--)
{
n = readint();
d = readint();
init();
ll m2 = n - 1;
m2 = (m2 + 1) * (m2) / 2;
ll m1 = 0ll;
int now = 2;
int cnt = 1;
repd(i, 2, n)
{
if (i + now - 1 <= n)
{
i += now - 1;
m1 += 1ll * now * cnt;
now <<= 1;
cnt++;
} else
{
m1 += 1ll * (n - i + 1) * cnt;
break;
}
}
if (d < m1 || d > m2)
{
printf("NO\n");
} else
{
repd(i, 2, n)
{
son[i - 1][0] = i;
}
int id = n;
while (dfs(1, 0, 0) != d)
{
int flag = 1;
int j = dep[id] - 2;
for (auto &i : v[j])
{
if (son[i][0] == 0)
{
if (son[fa[id]][0] == id)
{
son[fa[id]][0] = 0;
}
if (son[fa[id]][1] == id)
{
son[fa[id]][1] = 0;
}
son[i][0] = id;
flag = 0;
break;
} else if (son[i][1] == 0)
{
if (son[fa[id]][0] == id)
{
son[fa[id]][0] = 0;
}
if (son[fa[id]][1] == id)
{
son[fa[id]][1] = 0;
}
son[i][1] = id;
flag = 0;
break;
}
}
if (flag)
{
id--;
}
repd(i, 0, n)
{
v[i].clear();
}
}
printf("YES\n");
repd(i, 2, n)
{
printf("%d%c", fa[i], i == n ? '\n' : ' ' );
}
}
}
return 0;
}



