2018 ICPC上海大都会赛重现赛 D Thinking-Bear magic (几何)
2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 D Thinking-Bear magic (几何)
链接:https://ac.nowcoder.com/acm/contest/163/D来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
In order to become a magical girl, Thinking-Bear are learning magic circle.
He first drew a regular polygon of N sides, and the length of each side is a.
He want to get a regular polygon of N sides, and the polygon area is no more than L.
He doesn't want to draw a new regular polygon as it takes too much effort.
So he think a good idea, connect the midpoint of each edge and get a new regular polygon of N sides.
How many operations does it need to get the polygon he want?
输入描述:
The first line of the input is T(1≤ T ≤ 100), which stands for the number of test cases you need to solve.The first line of each case contains three space-separated integers N, a and L (3 ≤ N ≤ 10, 1 ≤ a ≤ 100, 1 ≤ L ≤ 1000).
输出描述:
For each test case, output a single integer.
示例1
输入
[复制](javascript:void(0)😉
1
4 2 3
输出
[复制](javascript:void(0)😉
1
题意:
给定一个正n边形,每个边的边长为a。
设当前多边形的面积为S,如果S<=L,就结束,
否则就要把这个正n边形变为的每一个边的中点连起来的图形。
如果S<=L,就结束,否则继续上面的操作,问最少需要操作多少次可以满足S<=L
思路:
我们应该知道正n边形变为的每一个边的中点连起来的图形还是正n边形,只是边长变小了。
我们只需要推算一下每次边长a变化后的边长newa的关系即可。
正n边形的面积可以通过分解为n个全等的等腰三角形面积的sum和来计算。
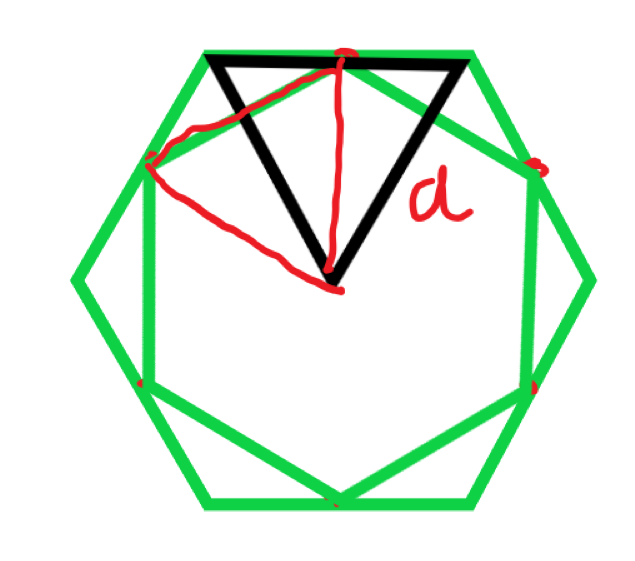
通过上图我们可以发现,圆图形分解的三角形的高h,在图形变化后等于新图形分解三角形的腰。
而三角形的各个角的角度并没有变化,只是边长变了,我们就一直迭代三角形边长求总面积即可。
因为数据范围不是很大,所以直接暴力迭代即可。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {a %= MOD; if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline void getInt(int *p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int t;
double n;
double a;
double s;
const double pi = acos(-1);
int main()
{
//freopen("D:\\code\\text\\input.txt","r",stdin);
//freopen("D:\\code\\text\\output.txt","w",stdout);
du1(t);
while (t--) {
scanf("%lf %lf %lf", &n, &a, &s);
int ans = 0;
double berta = 360.0 / n / 180.0 * pi ;
double certa = (pi - berta) * 0.5;
do {
double x = (0.5 * a) / cos(certa);
double h = x * sin(certa);
double now = n * 0.5 * a * h;
if (s - now > 0) {
break;
} else {
a = 2.0 * h * cos(certa);
}
} while (++ans);
printf("%d\n", ans );
}
return 0;
}
inline void getInt(int *p)
{
char ch;
do {
ch = getchar();
} while (ch == ' ' || ch == '\n');
if (ch == '-') {
*p = -(getchar() - '0');
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 - ch + '0';
}
} else {
*p = ch - '0';
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 + ch - '0';
}
}
}



