Rectangle Puzzle CodeForces - 281C （几何）

You are given two rectangles on a plane. The centers of both rectangles are located in the origin of coordinates (meaning the center of the rectangle's symmetry). The first rectangle's sides are parallel to the coordinate axes: the length of the side that is parallel to the Ox axis, equals w, the length of the side that is parallel to the Oy axis, equals h. The second rectangle can be obtained by rotating the first rectangle relative to the origin of coordinates by angle α.

Your task is to find the area of the region which belongs to both given rectangles. This region is shaded in the picture.

Input
The first line contains three integers w, h, α (1 ≤ w, h ≤ 106; 0 ≤ α ≤ 180). Angle α is given in degrees.

Output
In a single line print a real number — the area of the region which belongs to both given rectangles.

The answer will be considered correct if its relative or absolute error doesn't exceed 10 - 6.

Examples
Input
1 1 45
Output
0.828427125
Input
6 4 30
Output
19.668384925
Note
The second sample has been drawn on the picture above.

思路：

根据对称性，

我们把矩阵转化为w>=h 形状的。

又根据对称性，

如果角度a是钝角，可以把a变为与a互补的锐角，不影响答案值。

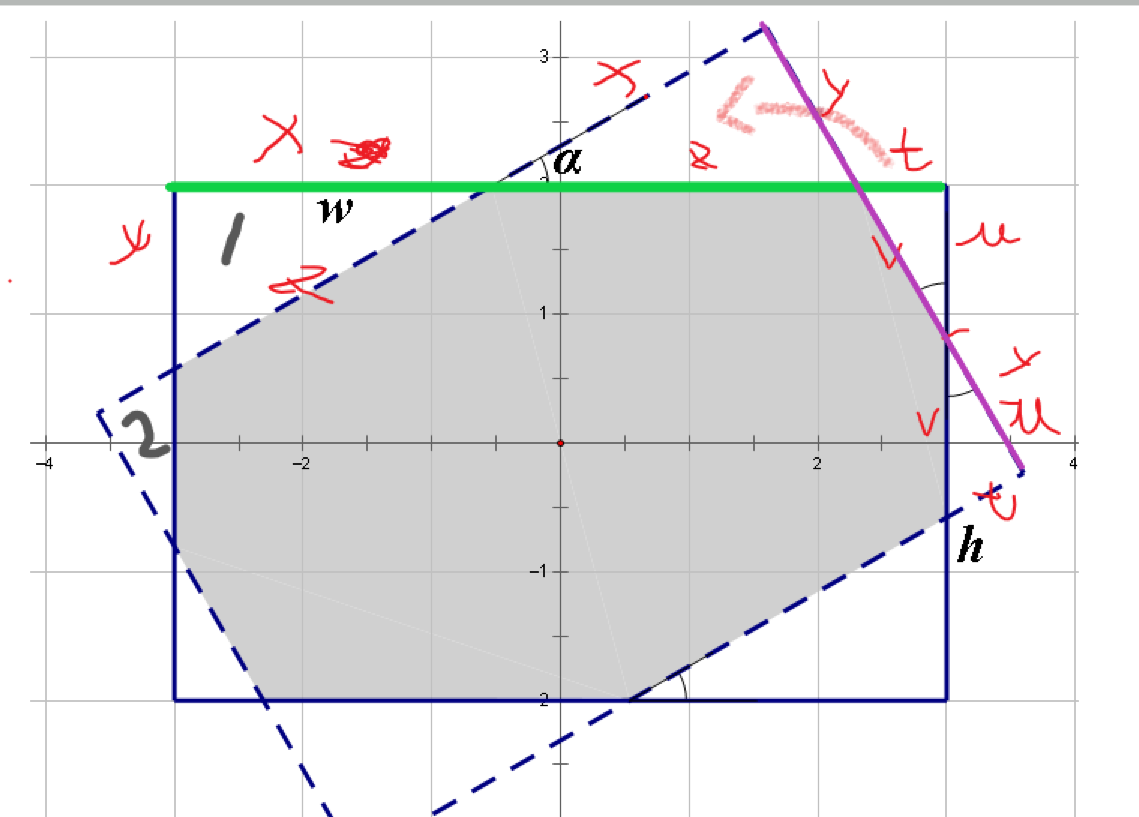
如图所示，我们只需要三角形1和2的面积就可以求的阴影部分面积，

那么根据绿色的线我们可以得出

x+z+t=w

根据紫色的线我们可以的出：

y+v+u=h

而根据三角形关系

我们可以得到 x，y与z的关系，u，t与v的关系。

两个方程，两个未知量（z，v）可以求出z和v，从而可以得出答案。

还有一个需要特殊判断的情况是：

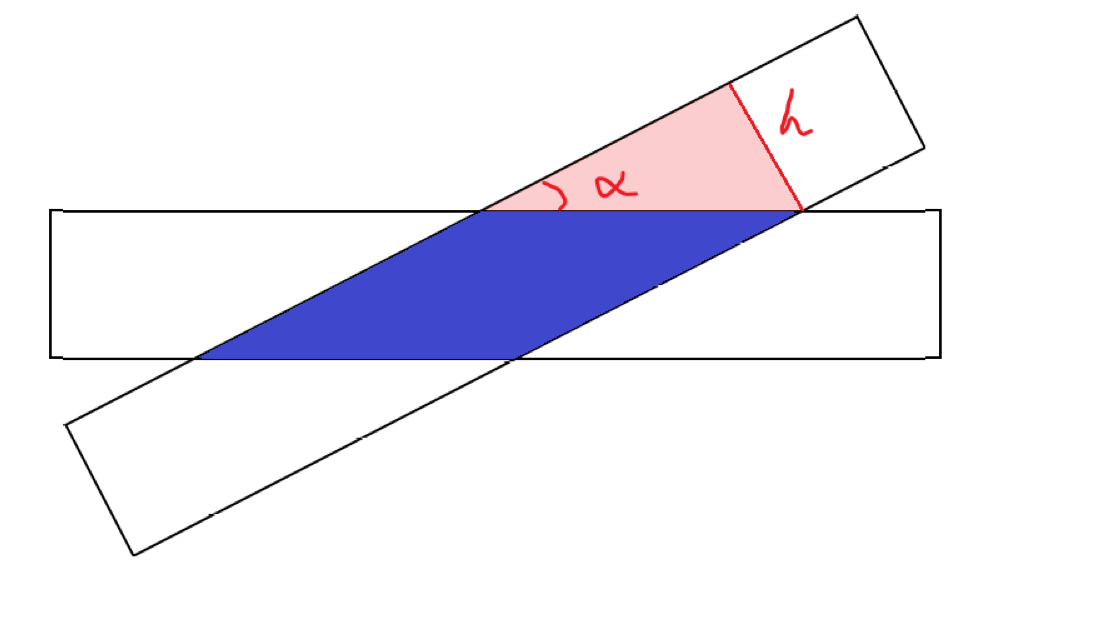
这种阴影部分的面积是一个蓝色的菱形，那么我们根据粉红色区域的三角形关系可以的出答案。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2) { ans = ans * a % MOD; } a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int *p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
typedef long double ld;
ld w, h, a;
const ld pi = acos(-1);
int main()
{
    //freopen("D:\\code\\text\\input.txt","r",stdin);
    //freopen("D:\\code\\text\\output.txt","w",stdout);
    cin >> w >> h >> a;
    if (h > w) {
        swap(h, w);
    }
    a = min(a, 180.0 - a);
    a /= 180;
    a *= pi;
    ld z = (w - (h * sin(a)) / (1.0 + cos(a))) / (1.0 + cos(a) - sin(a) * sin(a) / (1 + cos(a)));
    ld v = (h - z * sin(a)) / (1.0 + cos(a));
    if (v > 0.0) {
        ld x = z * cos(a);
        ld y = z * sin(a);
        ld ans = w * h;
        ans -= x * y;
        x = v * cos(a);
        y = v * sin(a);
        ans -= x * y;
        cout << fixed << setprecision(7) << ans << endl;
    } else {
        v = h / sin(a);
        ld x = v * cos(a / 2.0);
        ld y = v * sin(a / 2.0);
        ld ans = x * y * 2.0;
        cout << fixed << setprecision(7) << ans << endl;
    }

    return 0;
}

inline void getInt(int *p)
{
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    } else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}