2019牛客暑期多校训练营（第一场） B Integration （数学）

链接：https://ac.nowcoder.com/acm/contest/881/B
来源：牛客网

Integration
时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 524288K，其他语言1048576K
64bit IO Format: %lld
题目描述
Bobo knows that
∫
∞
0
1
1
+
x
2

d
x

π
2
.
∫0∞11+x2 dx=π2.

Given n distinct positive integers
a
1
,
a
2
,
…
,
a
n
a1,a2,…,an, find the value of
1
π
∫
∞
0
1
∏
n
i

1
(
a
2
i
+
x
2
)

d
x
.
1π∫0∞1∏i=1n(ai2+x2) dx.

It can be proved that the value is a rational number
p
q
pq.
Print the result as
(
p
⋅
q
−
1
)
mod
(
10
9
+
7
)
(p⋅q−1)mod(109+7).
输入描述:
The input consists of several test cases and is terminated by end-of-file.

The first line of each test case contains an integer n.
The second line contains n integers
a
1
,
a
2
,
…
,
a
n
a1,a2,…,an.

1
≤
n
≤
10
3
1≤n≤103
*
1
≤
a
i
≤
10
9
1≤ai≤109
*
{
a
1
,
a
2
,
…
,
a
n
}
{a1,a2,…,an} are distinct.

• The sum of
  n
  2
  n2 does not exceed
  10
  7

输出描述:
For each test case, print an integer which denotes the result.
示例1
输入
复制
1
1
1
2
2
1 2
输出
复制
500000004
250000002
83333334

题意：

思路：

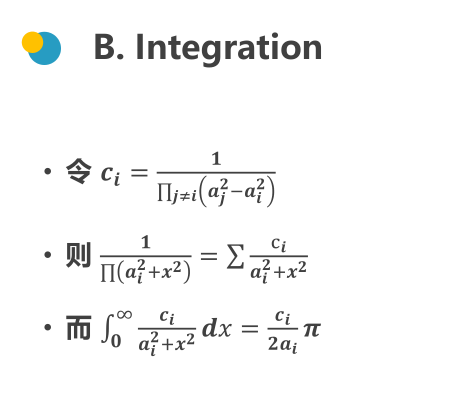
事实上我并不会上面的处理，真正积分的话要用裂项相消来出来。

但是有强大的自动积分软件啊: https://www.wolframalpha.com/

输入一个n=5的 情况，就可以看出规律。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
ll a[maxn];
int n;
const ll mod = 1e9 + 7;
int main() {
	//freopen("D:\\code\\text\\input.txt","r",stdin);
	//freopen("D:\\code\\text\\output.txt","w",stdout);
	gbtb;
	while (cin >> n) {
		repd(i, 1, n) {
			cin >> a[i];
		}
		ll ans = 0ll;
		repd(i, 1, n) {
			ll sum = 1ll;
			repd(j, 1, n) {
				if (i != j)
					sum = sum * ((a[j] * a[j] - a[i] * a[i]) % mod) % mod;
			}
			// sum = (sum + mod) % mod;
			sum = (sum * a[i]) % mod;
			sum = (sum * 2ll) % mod;
			sum = powmod(sum, mod - 2ll, mod);
			ans = (ans + sum) % mod;

		}
		ans = (ans + mod) % mod;
		cout << ans << endl;
	}

	return 0;
}

inline void getInt(int* p) {
	char ch;
	do {
		ch = getchar();
	} while (ch == ' ' || ch == '\n');
	if (ch == '-') {
		*p = -(getchar() - '0');
		while ((ch = getchar()) >= '0' && ch <= '9') {
			*p = *p * 10 - ch + '0';
		}
	} else {
		*p = ch - '0';
		while ((ch = getchar()) >= '0' && ch <= '9') {
			*p = *p * 10 + ch - '0';
		}
	}
}