Educational Codeforces Round 55 (Rated for Div. 2) D. Maximum Diameter Graph （构造图）

D. Maximum Diameter Graph
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Graph constructive problems are back! This time the graph you are asked to build should match the following properties.

The graph is connected if and only if there exists a path between every pair of vertices.

The diameter (aka "longest shortest path") of a connected undirected graph is the maximum number of edges in the shortest path between any pair of its vertices.

The degree of a vertex is the number of edges incident to it.

Given a sequence of n integers a1,a2,…,an construct a connected undirected graph of n vertices such that:

the graph contains no self-loops and no multiple edges;
the degree di of the i-th vertex doesn't exceed ai (i.e. di≤ai);
the diameter of the graph is maximum possible.
Output the resulting graph or report that no solution exists.

Input
The first line contains a single integer n (3≤n≤500) — the number of vertices in the graph.

The second line contains n integers a1,a2,…,an (1≤ai≤n−1) — the upper limits to vertex degrees.

Output
Print "NO" if no graph can be constructed under the given conditions.

Otherwise print "YES" and the diameter of the resulting graph in the first line.

The second line should contain a single integer m — the number of edges in the resulting graph.

The i-th of the next m lines should contain two integers vi,ui (1≤vi,ui≤n, vi≠ui) — the description of the i-th edge. The graph should contain no multiple edges — for each pair (x,y) you output, you should output no more pairs (x,y) or (y,x).

Examples
inputCopy
3
2 2 2
outputCopy
YES 2
2
1 2
2 3
inputCopy
5
1 4 1 1 1
outputCopy
YES 2
4
1 2
3 2
4 2
5 2
inputCopy
3
1 1 1
outputCopy
NO
Note
Here are the graphs for the first two example cases. Both have diameter of 2.

d1=1≤a1=2
d2=2≤a2=2
d3=1≤a3=2

d1=1≤a1=1
d2=4≤a2=4
d3=1≤a3=1
d4=1≤a4=1

题意：
给你一个数组a[i] ，代表节点i的入度上限值，让你构造一个符合数组a的图，要求图的直径最大（任意两个节点的最短 路中的最大值是图的直径），不能合法的联通图，就输出no，否则输出yes和图的直径，还有你构建图的边。
思路：

分析我们知道，如果a[i] 的sum和 小于 2*n-2 是无法构建出一个连通图的。直接输出no

先根据节点的入度上限降序来对节点排序，把a[i]>=2 的节点，都连成一条线，如果还剩a[i] = 1 的节点，选择2个扔到刚刚构建的线的首尾（如果就一个的话，就扔一个到首或者尾部即

可），如果还剩就找入度还有剩余的节点随便加入（对图的直径已经没影响了。） 则图的直径就是那条线的长度。（官方题解用竹子来描述要构造出的图，我觉得还是很恰当的。）

画个图就理解了。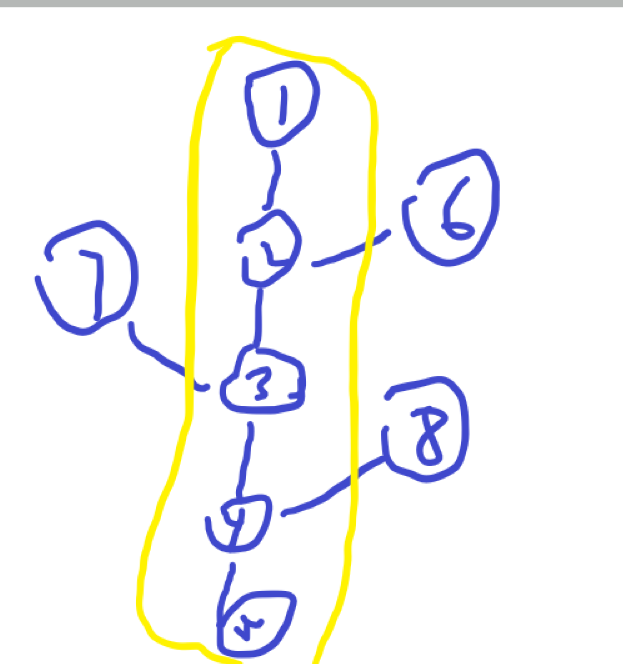

黄色圈的是竹子的主干（也就是影响直径的部分） 以外的点是竹子的叶子，不影响直径。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
struct node
{
	int id;
	int num;
} a[maxn];
bool cmp(node aa , node bb)
{
	return aa.num > bb.num;
}
int main()
{
	//freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
	//freopen("D:\\common_text\code_stream\\out.txt","w",stdout);
	int n;
	gbtb;
	cin >> n;
	ll sum = 0ll;
	repd(i, 1, n)
	{
		cin >> a[i].num;
		a[i].id = i;
		sum += a[i].num;
	}
	if (sum < 2ll * n - 2ll)
	{
		return 0 * puts("NO");
	}
	sort(a + 1, a + 1 + n, cmp);
	int ans = 0;
	std::vector<pii> v;
	int j = -1;
	repd(i, 1, n - 1)
	{
		if (a[i].num >= 2)
		{
			ans++;
			v.push_back(mp(a[i].id, a[i+1].id));
		} else
		{
			j = i+1;
			break;
		}
	}
	int id = 1;
	if (j != -1)
	{
		v.push_back(mp(a[1].id, a[j].id));
		ans++;
		// a[1].num--;
		repd(i, j + 1, n)
		{
			if (a[id].num > 2)
			{
				a[id].num--;
				v.push_back(mp(a[id].id, a[i].id));
			} else
			{
				id++;
				if (a[id].num > 2)
				{
					a[id].num--;
					v.push_back(mp(a[id].id, a[i].id));
				}
			}

		}
	}
	cout<<"YES "<<ans<<endl;
	cout<<sz(v)<<endl;
	for(auto x:v)
	{
		cout<<x.fi<<" "<<x.se<<endl;
	}
	return 0;
}

inline void getInt(int* p) {
	char ch;
	do {
		ch = getchar();
	} while (ch == ' ' || ch == '\n');
	if (ch == '-') {
		*p = -(getchar() - '0');
		while ((ch = getchar()) >= '0' && ch <= '9') {
			*p = *p * 10 - ch + '0';
		}
	}
	else {
		*p = ch - '0';
		while ((ch = getchar()) >= '0' && ch <= '9') {
			*p = *p * 10 + ch - '0';
		}
	}
}