数据挖掘：概念与技术--笔记1--度量数据的相似性与相异性

基本概念

数据矩阵

表示 n个对象 × p个属性

相异性矩阵

表示n个对象两两之间的临近度   n×n的矩阵

d(i,j)表示对象i与对象j之间的相异性

1 标称属性的临近性度量

计算公式：

m: 匹配的数目（即i和j取值相同状态的属性数）

p:  刻画对象的属性总数

令p=1 （主要目的是使相异矩阵的值在[0,1]之间），相同时为1，不同时为0

相异矩阵为：

相似性：

 

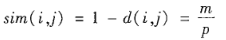
2 二元属性的临近性度量

（1）对称的二元相异性

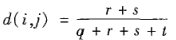
其中q,r,s,t的含义见表2.3

 

（2）非对称的二元相异性

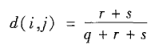
可以看出非对称的二元相异性是忽略t的，即忽略属性均为0的

例：

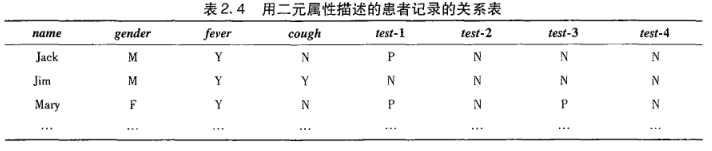
y(yes) p(positive) 值为1，n(no, negative) 值为0

其中name是对象标示符，gender是对称属性，其余均为非对称属性

对于非对称属性进行计算：

d(Jack,Jim)=(1+1)/(1+1+1)=0.67

d(Jack,Mary)=(0+1)/(2+0+1)=0.33

d(Jim,Mary)=(1+2)/(1+1+2)=0.75

 

3 数值属性的相异性

 介绍几个基本概念

一般计算距离之前数据应该规范化

欧几里得距离

 

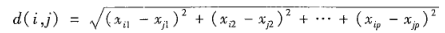
加权的欧几里得距离

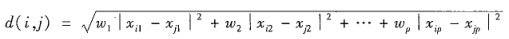
曼哈顿（城市块）距离

 

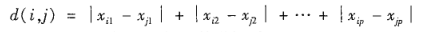
闵可夫斯基距离

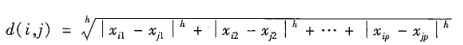
其中h是实数 h≥1

上确界距离

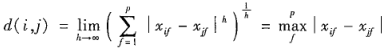
 （1）序数属性的临近性度量

计算步骤：

第一步：把test-2的每个值替换为它的排位，则四个对象将分别被赋值为3,1,2,3

第二步：按照公式 M_f表示总的排位，r_if表示第i个对象的排位 （此公式的目的是将每个属性的值域映射到[0.0,1.0]）

所以排位1的值为0,排位2的值为0.5，排位3的值为1

第三步：可以使用比如欧几里得距离算出相异性矩阵

（2）数值属性的临近性度量

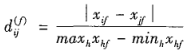
对test-3计算

max_hx_h=64,min_hx_h=22

 

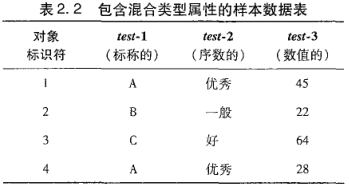
4 混合类型属性的相异性

 把所有有意义的属性转换到共同的区间[0.0,1.0]上

 

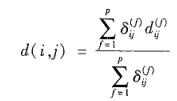
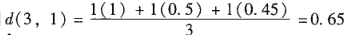
结果

 

 5 余弦相似性

对于稀疏矩阵，例比较文档或针对给定的查询词向量对文档排序

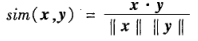
例：