迁移学习：
将已经经过大量数据集训练完成的模型套用，修改最后一个两个层级的超参数，这是在对于新的学习任务数据量差距很大的时候可适用的方式，但是要处理的大概是同一方向的东西，例如图像对图像的迁移学习，语音对语音的迁移学习，如果说新任务的数据量也很客观，可以选择重新训练整个模型的超参数；所谓预学习,微调，就是迁移学习，对其层数的微改动与超参数的调整范围，最主要的原因还是缺少训练数据；
---------------------------------------------------------------------------------------------------------------------------
多任务学习：
不再是单一输出一个y预测一个单一物件，比如还可以增加y的维度，让其在同一模型中可以预测不同的东西，比如在路上一张照片输入，同时预测图片上是否有行人，是否有车辆，红绿灯，警示牌等等，不再像之前的预测猫咪，单一只看是否存在猫咪；对于一块相近事物的多任务学习或许会比单任务学习更好提升模型预测能力，因为这些东西是相互关联的，在学习调整超参数的同时，相辅相成；
---------------------------------------------------------------------------------------------------------------------------
端对端学习方式与传统学习方式：
在数据量不是很大适中的时候可以选择使用传统的学习方式，手搓每个流程的运行函数，当数据量大的时候选择使用端对端的学习方式，所谓端对端就是省略中间运行的过程都封装完毕，只用一个输入就会有一个输出；
-----------------------------------------------------------------------------------------------------------------------------------
卷积神经：
过滤器（核）：
运算方式，将图片与核按区域相乘相加，最后得到一个点位的总值；
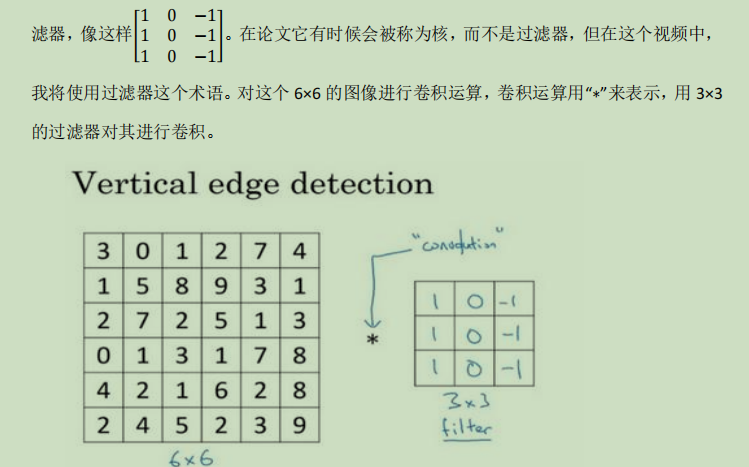
比如对一个6x6的图片进行垂直检测，可以设置一个3x3的过滤器，过滤完后新的矩阵会有在两种不同的区间有一个明显的区别；
垂直检测：检测出垂直部分不同的地方，比如一片明一片按的图片，按照垂直检测的方式卷积运算可以得到一个新图片，中间一块是明显的代表分界线，
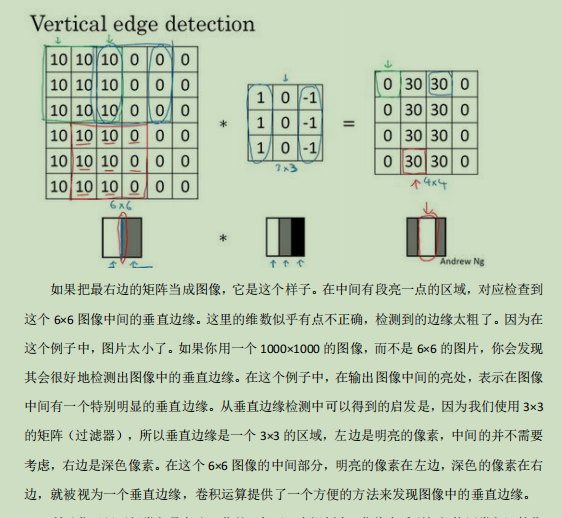
一般是将过滤器内部数字作为超参数，让模型自己训练得到超参数，当然也存在了很多总不同的过滤器，
Padding:
如果按照上述的方式进行检测会发现一个问题：靠近中间的方块值使用的次数会比边缘的次数多，那么边缘的特征使用得相对较少，会使得信息丢失，所以可以使用填充边缘得方式使得边缘的方块不位于边缘，可以同样多次使用，这种填充边缘的方式叫做same卷积，不填充的方式叫valid卷积,在valid卷积的情况下如果设图片矩阵维度为NxN，过滤器的矩阵维度为FxF，那么经过卷积运算后新矩阵的维度为（N-F+1）*（N-F+1）；经过卷积后的矩阵是缩小的也进一步表明了信息的丢失，在后续只会放大这种情况，不一定好，对于same卷积，假设填充值为p，四个角每个角都增加p个方块，那么新的矩阵为（N+2p-F+1）*（N+2p-F+1），可以通过调整p的值使得新矩阵大小与原图片大小相同；
卷积步长（strided）：
简单来讲就是原本我们卷积移动是按照一格一格位置的移动进行卷积计算，我们可以对他的移动做出设置，让他一次性移动多一点，一次移动三格四格之类的。
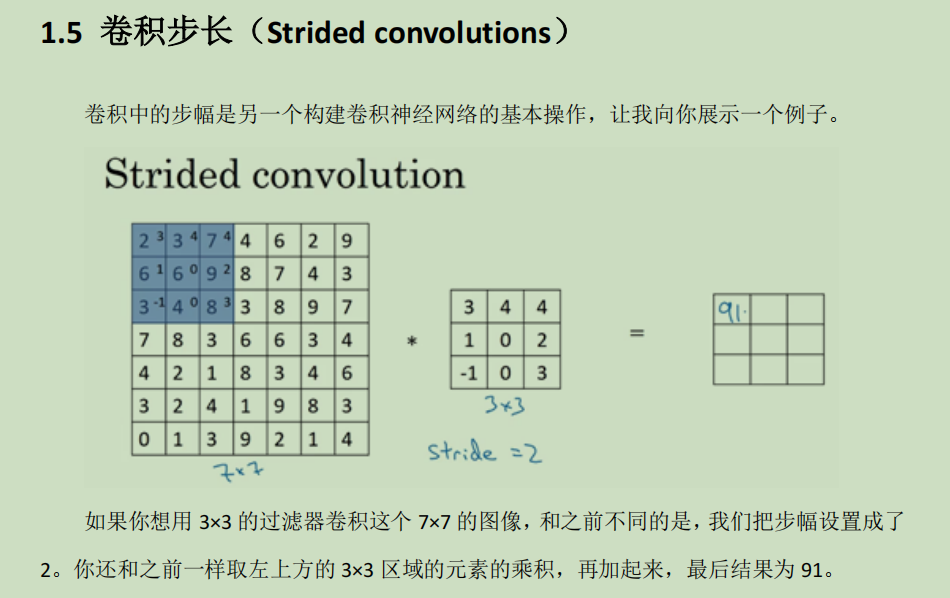
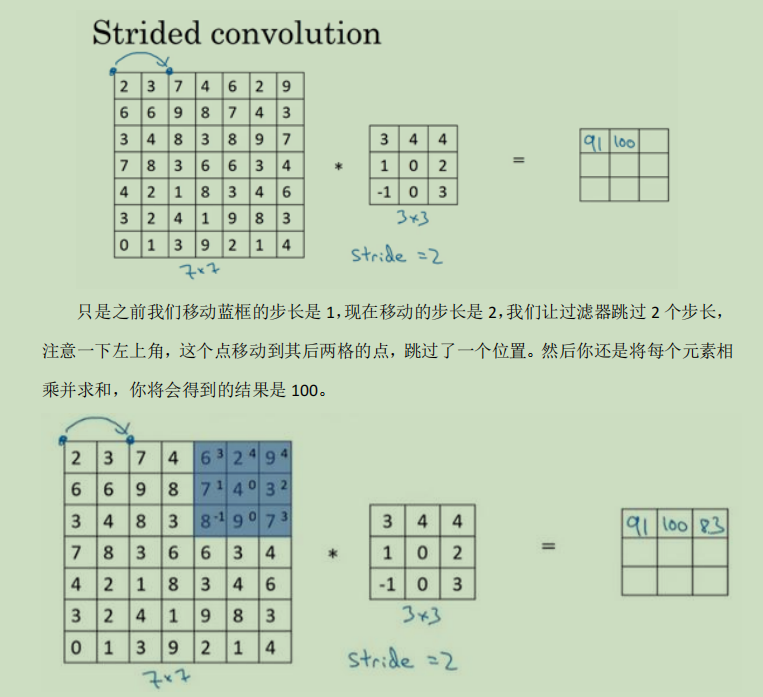
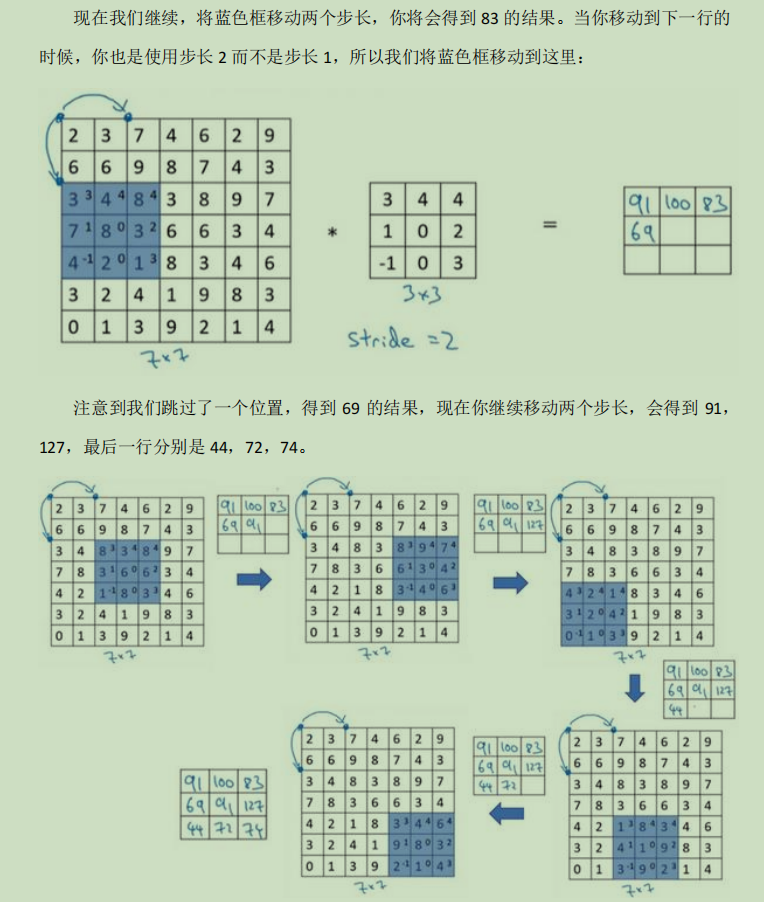
上面的图片只是想举一些例子，进行卷积处理时步长对输出结果的影响，那么下图就是给一个输出的计算公式：
立体卷积：
上述的只是对于平面的二维数组进行卷积而言，对于图片来说可以利用他的RBG三原色进行卷积处理，将RGB视为分为三个平面，三个平面点位叠加在一起就是一个点的颜色，那么就也可以使用一个三维的核进行处理：
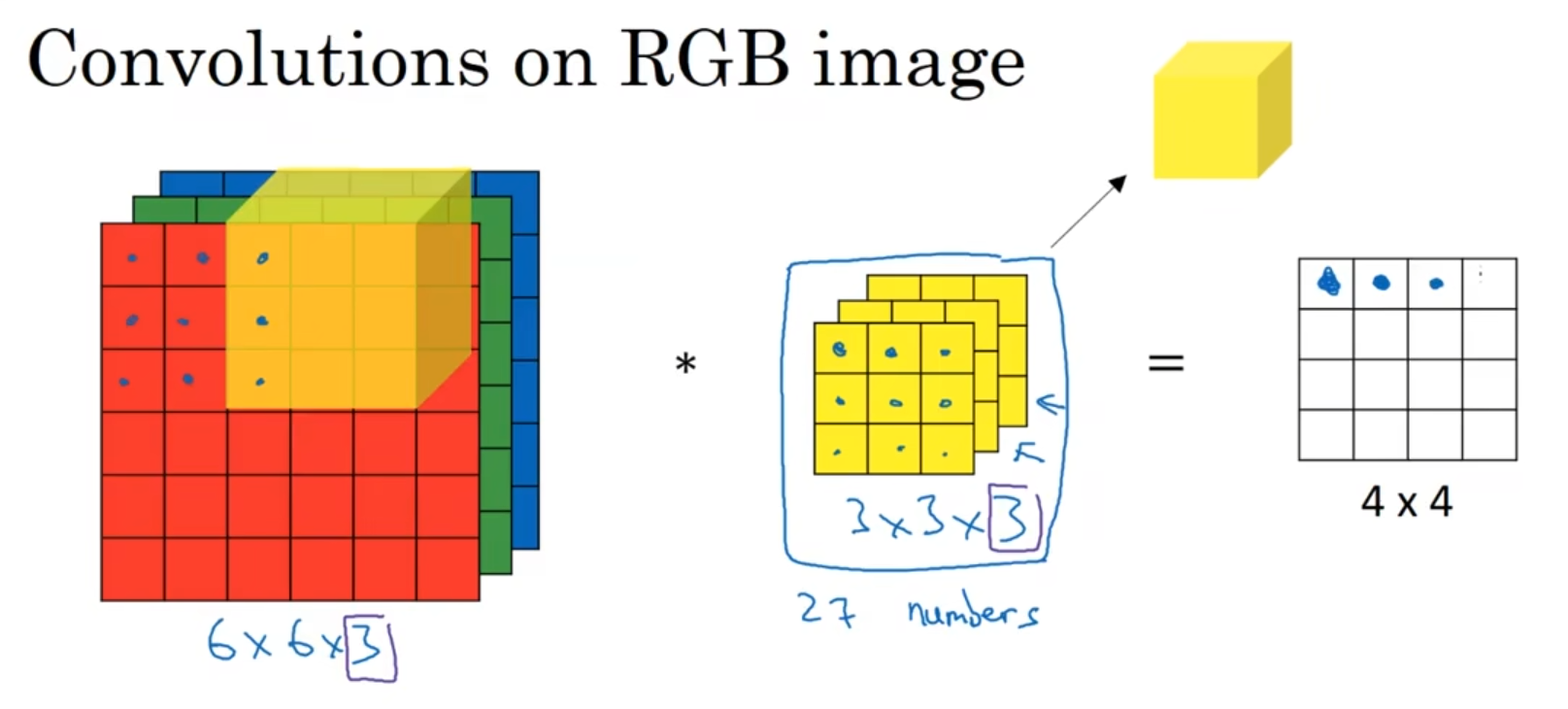
将左图对应的位置与核的每一个位置进行乘积再相加，最后得出一个平面的每个位置上的值，同样对于核的不同设置也会出现不同情况，在这里结果是二维的，因为核的通道数是等于图像的通道数的；
这里要注意的核的使用：好像说什么核的通道个数要等于图片的通道个数。
对于核的设定主要看你的作用是什么，如果你是想做垂直边缘检测那么就可以使用上面说的，将三维核每一个面都设置成下图的参数，进行垂直检测
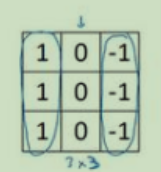
但是如果你只在乎对于RGB一个图层的边缘检测例如你只在乎对红色层面的边缘检测，那么就只在核的红色维度设置成上图的参数，其余的维度都设置为0；
如果你不单单想进行垂直检测，可能还想进行水平的边缘检测，斜着的边缘检测，可以多设置几个核，将核卷积的结果得出进行叠加得到一个新的立方体
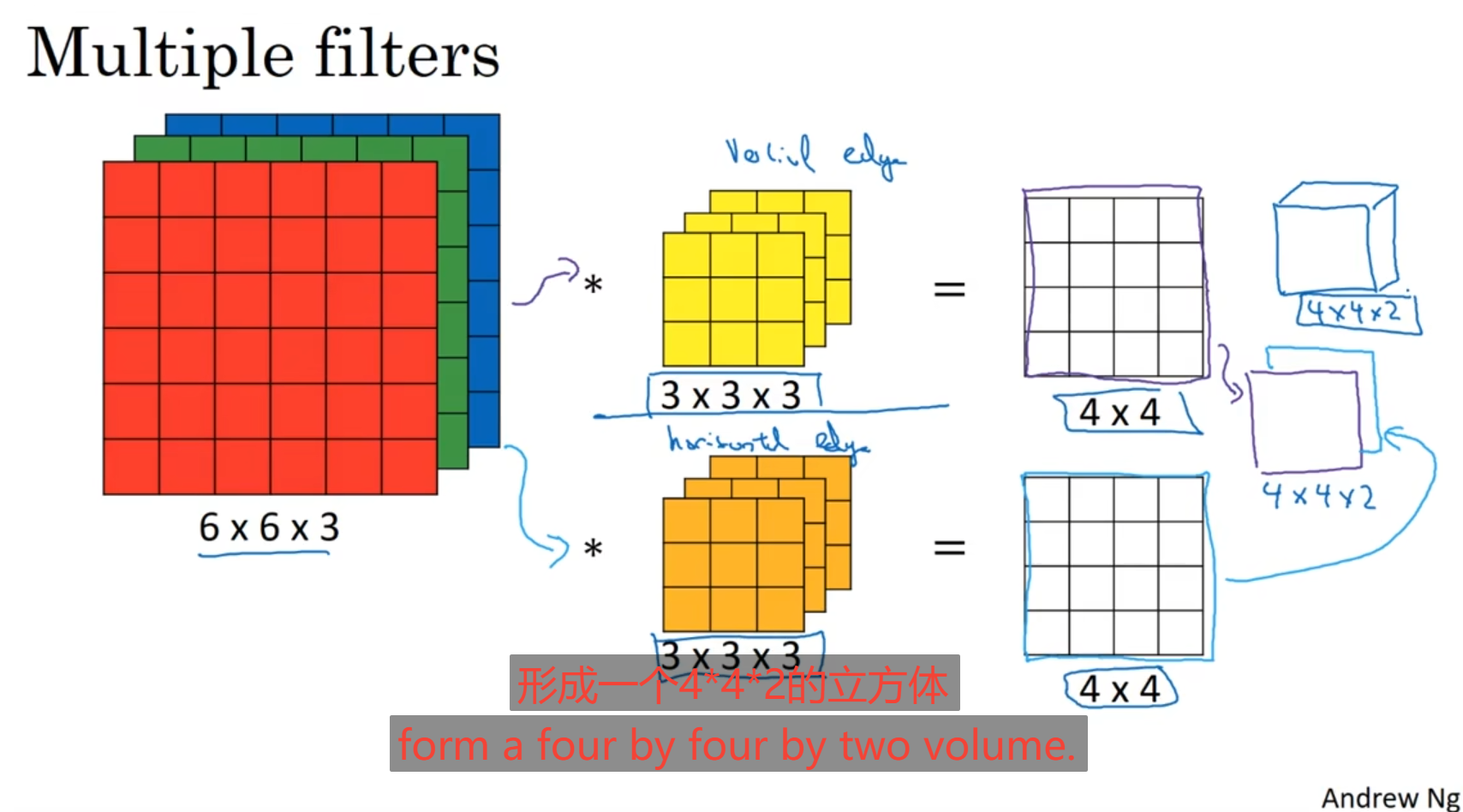
对于一层中卷积层的情况：例如在l层中
使用fl表示过滤器（核）的大小尺寸f*f
使用pl代表padding的值，就是要不要增加空白边框作为图片的一部分
使用sl表示步长
使用nl表示过滤器（核）的数量
对于输入的卷积使用nhl-1表示其高度，nwl-1表示其宽度，ncl-1表示其通道数，至于为什么是l-1因为这是上一层进行过滤得出的卷积，所以使用l-1，那么对于本层使用过滤得出的卷积就为l，对其宽度与高度计算就是相应的高度或者宽度加上2*padding减去过滤器的尺寸f一般过滤器好像都是正方的所以只用一个f就行，再除以步长，最后加一向下取整，这就是卷积的高或者宽维度；
池化层：
作用缩减模型大小，提高计算速度，同时提升计算的鲁棒性。
最大池化层：
提取一块区域内的最大值作为这个区域的特征值，直观理解就是从这个区域内提取的最大值可能就代表着这一个区域内的特征，如果说这个区域内不存在什么特征可能他们的值都很小很靠近；下面是一个2*2步长为2的过滤器，用于提取区域内最大值。
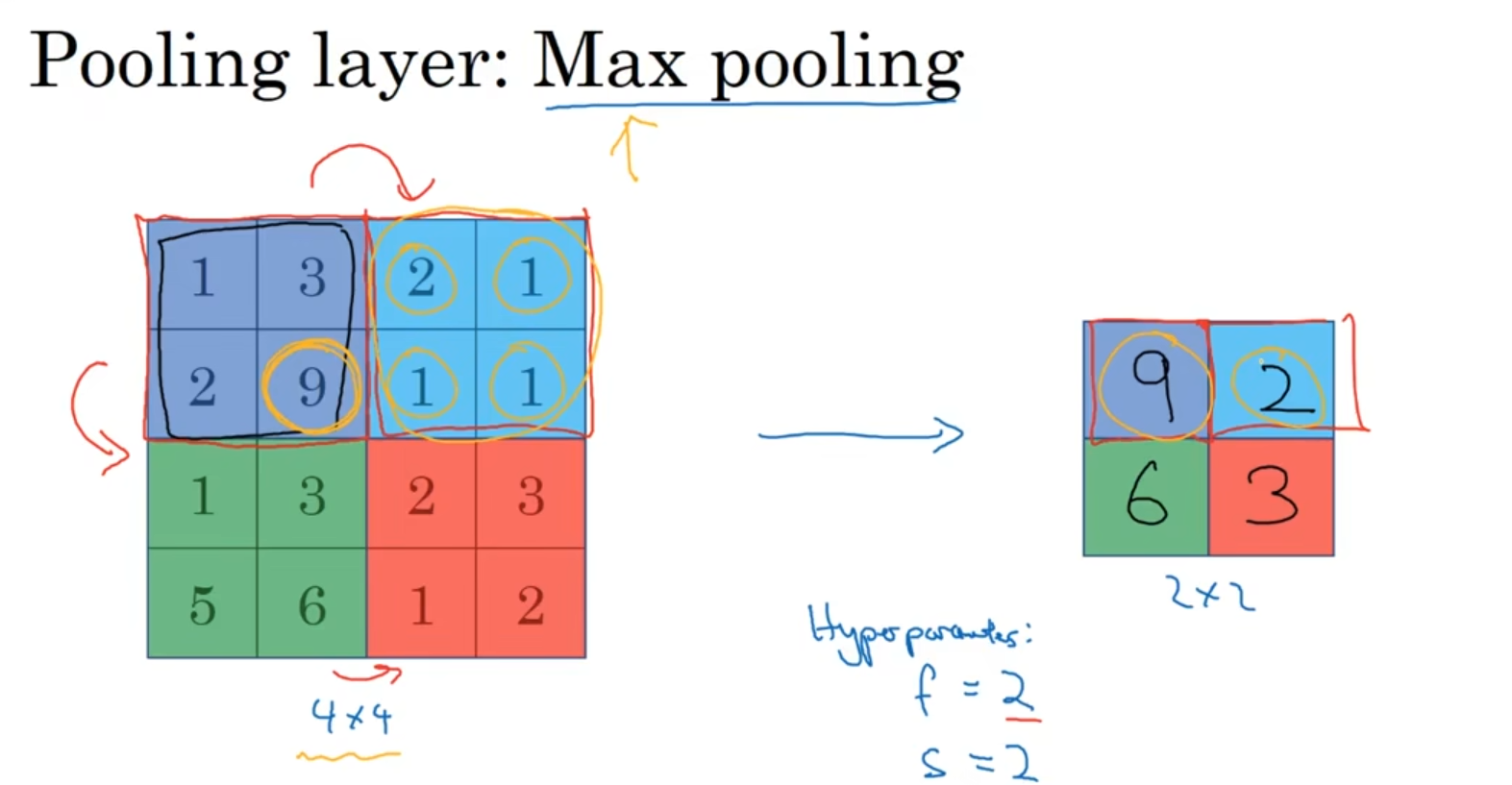
但是这玩意好像只是对二维进行一个筛选，就是说即使你是三维立体的，但是我每次也只对你一个通道进行最大池化计算，最后将每个通道池化结果再堆叠起来，通道数量是不会进行改变的。
除了最大池化算法还有平均池化算法之类的。
卷积神经网络，卷积神经网络和神经网络差不多，但是前面一段我们使用的是卷积，还可能夹杂着池化层，对于卷积的层数，我们只统计具有权重（w）与参数的网络层，而对于只有一些超参数并不具备权重的池化层不算做一层，对于一张图片来说卷积完后把维度展成一维，后面使用神经网络进行训练；
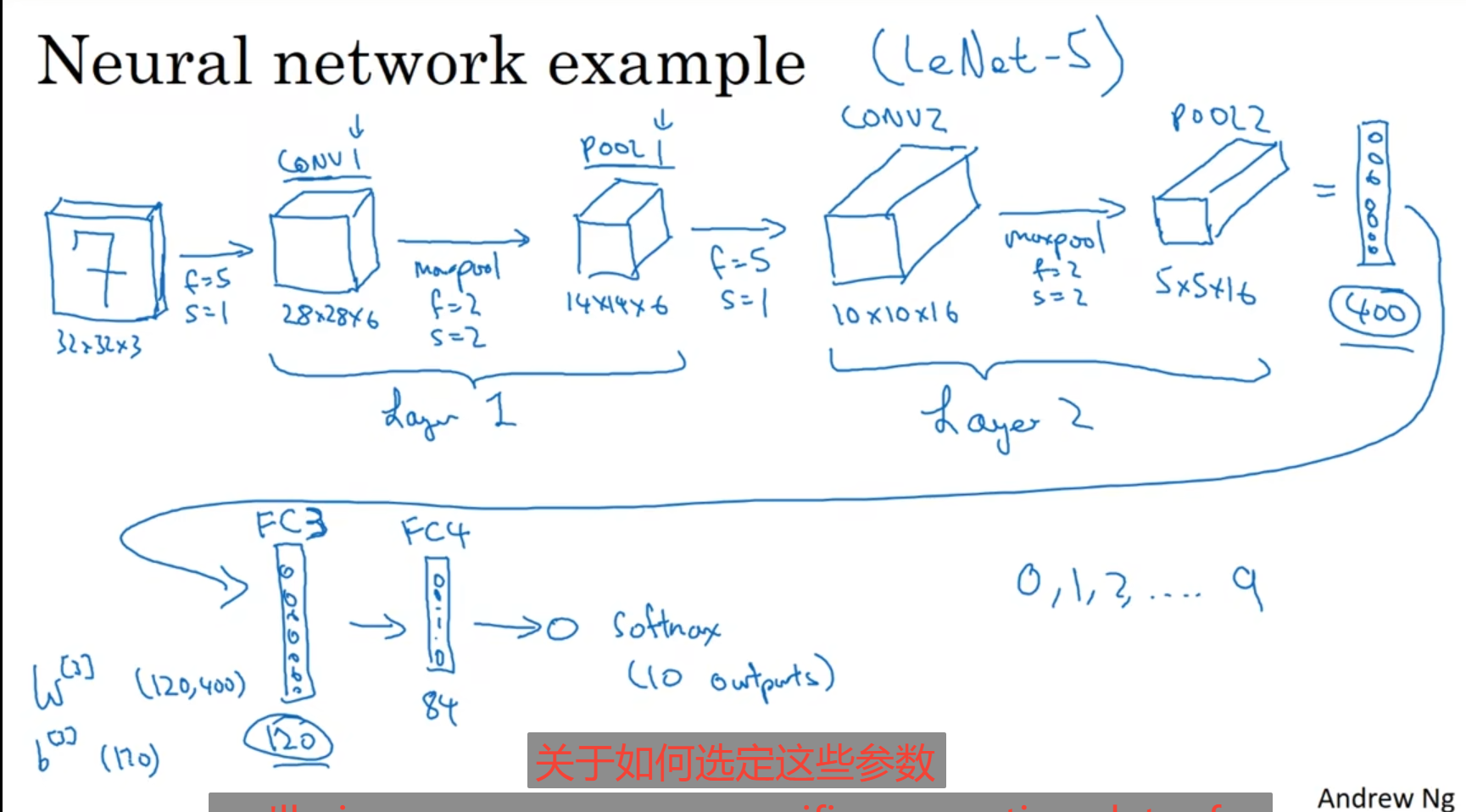
卷积使用的好处：
减少参数的设置：
1.参数共享：
进行卷积的时候对于一个特征进行提取如果是对于一部分的特征提取有效，那么对于整张图片提取也是有效的。
2.稀疏连接：
在使用卷积时设置核，核所覆盖的那一小块区域计算出来的值就只于那一小块存在关系；像下图中的第一个0卷积只与左边左上角那块小区域存在关系。这就是稀疏连接的大概意思。
神经网络可以通过上述的两种机制减少参数，以便我们使用更小的训练集进行训练，预防过拟合。
