学习率衰减：
在迭代到后期可能因为学习率的问题导致一直在一个大范围动荡无法更近一步靠近低点，所以要调整学习率以求达到低点，使用迭代次数自动衰减是挺好的办法；
遍历完一次训练集为一代
——————————————————————————————————————————————————————
为超参数选择合适范围：
对于一个二维超参数，可以想象成一个矩阵，在一个矩阵内随机选择点位，选择后进行测试，如果发现效果不错就以这个点位为中心缩小范围调整参数继续查找参数，一直找到最合适为止；
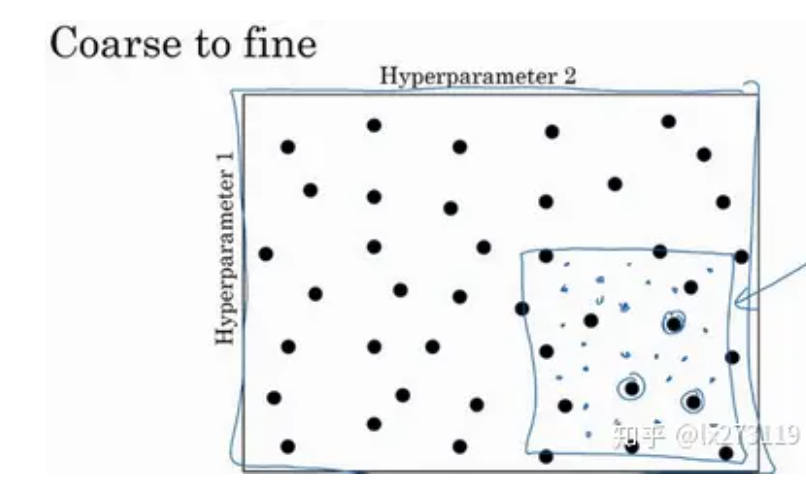
有的超参数适合随机，但是有的超参数不适合；对于学习率范围可能在0.0001到1之间，那么如果随机的化就是每个值概率相同，但是并不是这样处理的，因为这样处理0.1到1占比就是90%0.0001到1占10%，使用对数尺的方法进行调整；随机生成一个0到1的数字乘以-4作为10的次方就行，这样在0.0001-0.001-0.01-0.1-1之间概率都相同
除了学习率外，还有momentum与rmsprop的β，之前提到过这两个推荐的是0.9-0.999之间，但是就算使用对数尺也不好之间生成，所以就反算一下1-β，这样范围就是0.1-0.001之间，再去使用对数尺处理，最后将符号转化一下得到β；
超参数模式：
——————————————————————————————————————————————————————
batch norm（batch归一化）：讲的很详细，虽然我解释了为什么归一化了又还原，为了获取特征，既然要还原那么归一化不是多此一举吗；可能是经过归一化后数据挤压在一起，点位太近，放大平移作用利于泛化，扩大点之间的距离，更适合查找特征；
计算步骤
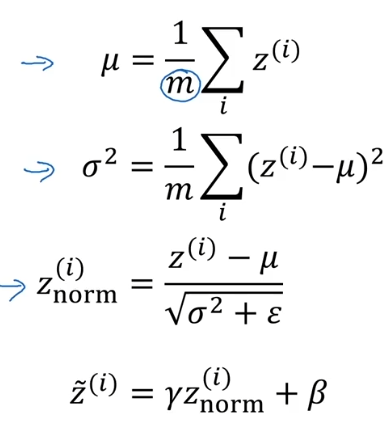
又好像说γ与β的值看自己所需要的值调整，经过归一化处理后z的均值为0，方差为1，而γ与β的作用是使得
新的z均值为β，方差为γ的平方，
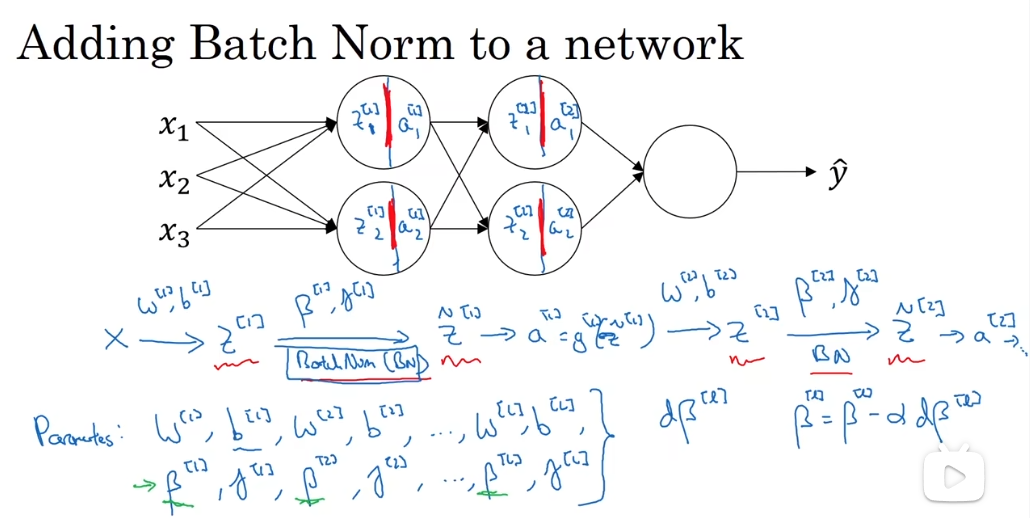
注意向前传播与向后传播对于新参数的更新
——————————————————————————————————————————————————————————————、
Softmax分类器：
对于处理多个预测结果的情况，在最后一步建立多个z的等式，将训练样本传入后出现多个不同的值，对值用于自然数e的次方上，最后求取总值，求出每个结果的占比，根据占比大小来判断，就是求最后结果占比大小
最后一层算出z的结果，新建一个t，用于归一后续放入激活函数
