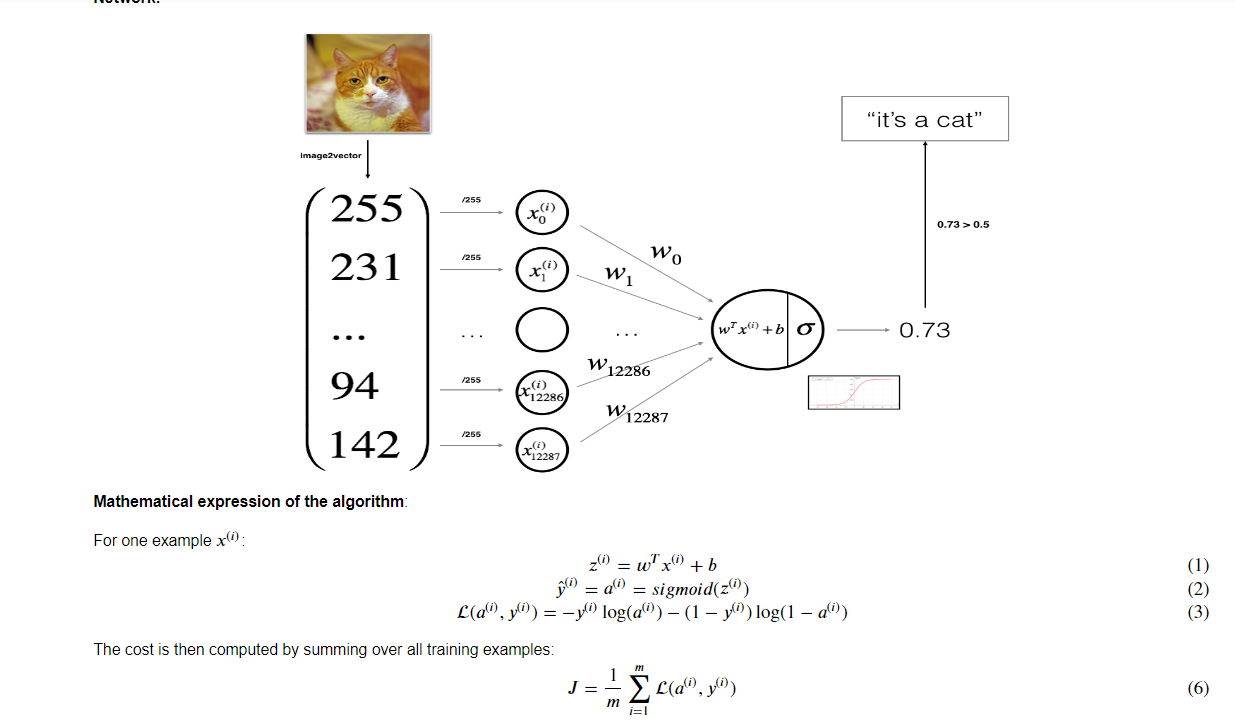
训练集处理：
在X_train塞入一个训练集例如209张照片，那么数组维度可能为（209，64，64，3）209张，高64，宽64，3层（RBG）
同时存在一个Y_train训练集的y值，
此时X_train.shap[0]为最外维度209；要一次性处理数据集最好将它变成二维数组把色层放一个维度X_train=X_train.reshape(209,-1);这个操作会把数组变为（209，12288）；
在处理训练集时统一默认处理一张照片占据一列所以再转置一下X_train=X_train.T;让其变为（12288，209）大小数组
一般会存在一个标准化处理，或者说规范处理，对于图片直接将数据集/255就好了，形成最后的向量测试集
如果a，b是两矩阵
np.dot(a,b)=矩阵乘法，但是根据公式求z每一张照片都应该对应一个实数而不是矩阵，z=w.T*X+b,因为训练集经过矩阵变幻操作，所以现在一列就是一张图片，在w.T+b操作时就会变成一个行向量，每列一个对应一张照片预测值，现在就获得一个Y_pre_train(预测值)
激活函数sigmoid:将初始的z值固定在(0，1）范围内，现在激活预测值都在（0，1）范围内
再去计算损失函数这样每张照片的损失值都在一个行向量内，对这个行向量求取期望（均值）就是损失成本；
对于Z函数内部的参数向量w与实数b初始化均为0，注意向量w的形状列向量（12288，1）后续才能与训练集相乘处理
这样只是开始了一次正向传播或者说初始正向传播，我们目标是更新迭代参数w与b，找到最合适的w与b使得成本（J）最低；误差最低
完成一次正向传播，
最主要目的是反向传播更新迭代w与b：
导数根据链式法则进行求导：
先求出这里的表达与平日高数中的表达有点不一样，da，dw，dz都是表示导数从头导到那个值的倒数，但是平日用的倒数是函数的标，这个是自变量的标不太好解释用多了就习惯了，刚开始有点不好转换过来；
对于单个训练样本根据链式法则计算出dz=a-y;a为单个预测值，y为训练结果的值，
w因为是矩阵内部的每一个w都需要求导最后才求得完整的dw矩阵，但是这里对dw进行了向量化（1，12288），注意前面求z的时候是使用w的转置（12288，1），与一张图片的向量化相同，两个向量直接使用“*”产生的结果就是对应位置上的值进行乘积；刚刚好就完成了单个训练样本的求导；
db就直接等于dz了
/**************************************************/
上面是一个训练样本的反向传播根据损失函数（L）导出
下面是整个训练集，根据下面的图片来看，因为整个训练集一起操作最终完成的是对成本函数(J)（损失函数的期望）的更新，所以对于训练集中每个训练样本训练出来的dw与db求期望就是成本函数的dw与db；
/**************************************************/
因为是对整个训练集进行处理所以dZ=A-Y_train;
dW=XdZ,db=dZ
此时dW应该是一个（209，12288）矩阵，里面每一列存放的是每张图片计算出来的损失函数（L）的dw的导数，我们目标是成本函数（J）的dw就一个列向量（1，12288）
成本函数是损失函数的期望，所以把，每一列的元素都加起来除以209就得出最新更新的dw；db同理；
使用操作dW=np.sum(dw,axis=0);但是这样会形成一个一维行向量，也可以使用
dW=np.dot(X,dZ.T)使用转置和矩阵乘法的方式直接完成最后除掉一个209就是要求成本函数（J）的dW，
对于db就直接np.sum（db）/209即可，这样就完成一个训练集的处理求出dW，db；
*********************************************////////
训练更新迭代方式：α是学习率，也是步长
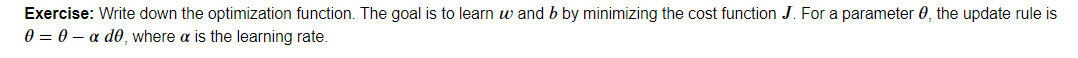
w=w-α（dw），b=b-α（db）；
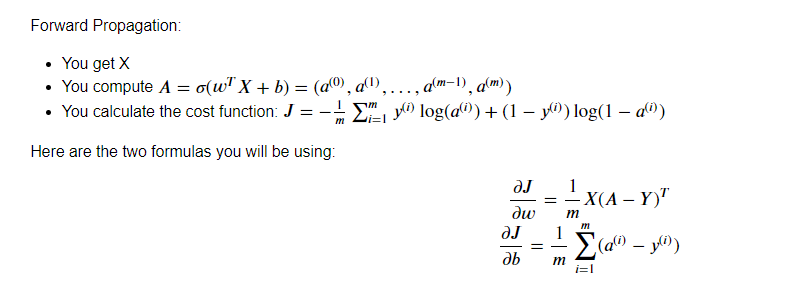
其中的A就相当于上面正向传播中的Y_pre_train(激活预测值)
根据上述的反向传播更新出w与b，继续正向传播，方向传播，一直迭代到最合适的w与b出现为止；
根据目标来看我们是要求出一个w与b使得成本函数达到最小，而反向传播进行更新需要A（Y_pre_train）所以才要一直正向反向传播；
对于w与b的更新公式：
w=w-α（dw），b=b-α（db）；
对于单一的维度来看，也就是把b或者w其中一个看作定量，更新另外一个的时候
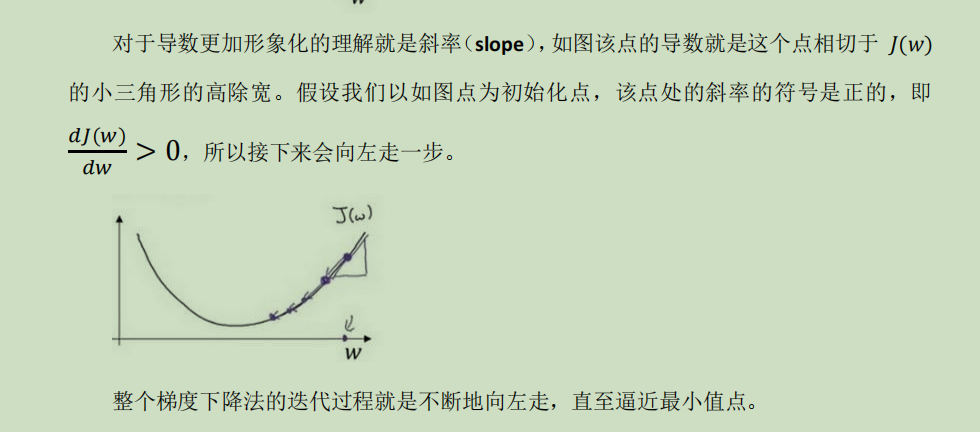
相当于一个近似的意思，就是求出每个点的斜率，根据设置的学习率反着走推回去找到那个最低点所在的位置，应该是相当于微分；
将上述的想法进行函数的封装，最后组合形成一个模型函数就完成了第二周作业
