Floyd 最短路径算法(天勤详解)
Dijkstra 是求某个顶点到其余各个顶点的最短路径。
Floyd 是求图中任意一对顶点间的最短路径。
过程
假设存在有向图,
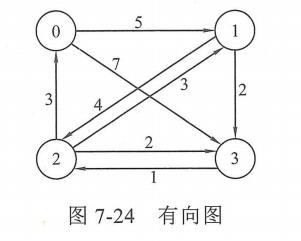
采用的存储结构是 邻接矩阵

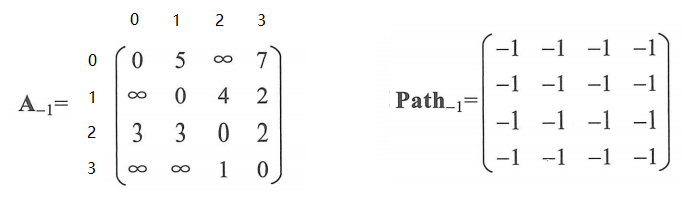
首先初始化 A[ ][ ] 方阵,

path[ ][ ] 方阵默认值为 -1
A 的下标代表第几个节点,-1 代表初始化节点
// 初始化for (i = 0; i < g.n; i++) { for (j = 0; j < g.n; j++) { A[i][j] = g.edges[i][j]; path[i][j] = -1; }} |
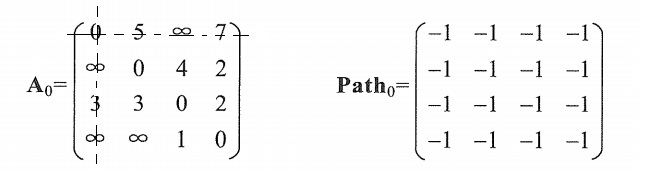
按照节点顺序依次遍历 k = 0 时
首先选择第一个, 以A[0[0]为基准做十字交叉线 X1,类比矩阵的余子式;除了此十字线以外的数字,
选择一个 A[i][j] 再做一个十字交叉 X2,与 X1 相交于两点 A[i][0]、A[0][j],判断:
if (A[i][j] > A[i][0] + A[0][j]){ A[i][j] = A[i][0] + A[0][j] path[i][j] = k; // 同时修改path, k此时为0} |
从上到下、从左到右依次对比 <=> 所有相邻的边
注意:如果A[i][j] 在以 A[0][0] 为基准的十字线上,就不需要进行比较。
方阵A 比较完后没有数字修改
k = 1 时,
以 A[1][1] 为为基准做十字交叉线,比对过程和上述一样。
只有 A[0][2] 修改条件成立,故 path[0][2] = k

同理 k = 2 时,从上至下、从左至右遍历,除了十字线上的
修改A[1][0]、A[3][0]、A[3][1]的值
对应path[1][0] = k、path[3][0] = k、path[3][1] = k

k = 3 时,,从上至下、从左至右遍历,除了十字线上的
修改A[0][2]、A[1][0]、A[1][2]
对应path[0][2] = k、path[1][0] = k、path[1][2] = k
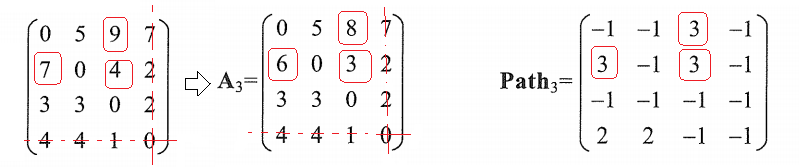
遍历结束。
以对上过程归纳可得天勤代码。
代码
void Floyd(MGraph * g, int &path[][maxsize], int A[][maxsize] ) { // 初始化 for (i = 0; i < g.n; i++) { for (j = 0; j < g.n; j++) { A[i][j] = g.edges[i][j]; path[i][j] = -1; } } for (k = 0; k < g.n; k++) { // 对节点遍历 for (i = 0; i < g.n; i++) { // 对方阵里的值枚举 for (j = 0; j < g.n; j++) { if( A[i][j] > A[i][k] + A[k][j] ) { // 修改条件 A[i][j] = A[i][k] + A[k][j]; path[][] = k; } } } } } |





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 智能桌面机器人:用.NET IoT库控制舵机并多方法播放表情
· Linux glibc自带哈希表的用例及性能测试
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 新年开篇:在本地部署DeepSeek大模型实现联网增强的AI应用
· DeepSeek火爆全网,官网宕机?本地部署一个随便玩「LLM探索」
· Janus Pro:DeepSeek 开源革新,多模态 AI 的未来
· 互联网不景气了那就玩玩嵌入式吧,用纯.NET开发并制作一个智能桌面机器人(三):用.NET IoT库
· 上周热点回顾(1.20-1.26)