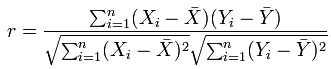Python机器学习(8)——推荐算法之推荐矩阵

每个人都会有这样的经历：当你在电商网站购物时，你会看到天猫给你弹出的“和你买了同样物品的人还买了XXX”的信息；当你在SNS社交网站闲逛时，也会看到弹出的“你可能认识XXX“的信息；你在微博添加关注人时，也会看到“你可能对XXX也感兴趣”；等等。

所有这一切，都是背后的推荐算法运作的结果。最经典的关联规则算法是大名鼎鼎的Apriori算法，源自一个超市购物篮的故事：啤酒总是和尿布一起被购买。有兴趣的可以去看看。

本章我们来学习一种最简单的推荐算法：推荐矩阵。虽然简单，但是却被广泛应用着。

1、推荐矩阵

为描述方便，以下我们以“购物推荐”作为背景进行介绍。假设你有个卖商品的网站，拥有每个用户购买每个物品的数据。现在，某个用户A购买了商品a，如何向他推荐他最有可能感兴趣的其他商品呢？

为达到这个目的，通常有两种思路：

1：寻找与该用户（A）购买习惯最为相似的用户（B)，认为B购买的物品，A也最有可能感兴趣。

这种情况适用于A已经购买过一些商品，算法能够根据A已经购买的物品作为特征，去匹配与A购买习惯最相近的用户。这种方式是以用户为中心的，推荐出来的商品b可能跟商品a风流马不相及，因此更适合于类似SNS和微博这样的平台，根据用户的已知兴趣集合来向其推荐其他具有相同兴趣的用户；

2：寻找与商品（a）最为相似的商品（b)，认为A既然对a感兴趣，也有可能对b感兴趣；

这种情况是以商品为中心的，因此更适合购物推荐这样的场景。

 而要计算两个向量“最相似”的程度，有很多方法，如KNN中用到的欧式距离，或者海明距离等。但是欧式距离并不适用于本场合。比如用户A购买了5个商品a，5个商品b，用户B购买了5个商品a，0个商品b，用户C购买了10个商品a，10个商品b，用距离来度量的结果必然是A与B更近。而实际上A跟C是极其相似的。

因此这里，我们介绍皮尔森相关系数(Pearson correlation coefficient)。其定义如下：

该系数定义的是两个向量的线性相关程度，取值范围为[-1,+1]，0表示线性无关，绝对值越大线性相关程度越大，正/负表示正/负线性相关。

简单的给几个例子：

[1,2,3]，[4,5,6]：1

[1,2,3]，[6,5,4]：-1

[1,2,3]，[1,2,4]：0.98

[1,2,3]，[-1,-11,-111]：-0.9

因此，我们将构造一个矩阵来描述用户购买商品的情况，该矩阵以用户为行、商品为列。要计算某个商品a最相似的商品，我们通过计算商品a所在的列与其他的每一列的皮尔森相关系数，找出最大的前N个推荐给用户即可。

2、测试数据

数据为一份简单的购物清单，每一行对应着用户id——商品id这样的数据对。如下图所示：

 

1 1 3
1 2 3
1 3 3
1 4 1
2 1 1
2 2 1
2 3 1
2 4 1
......

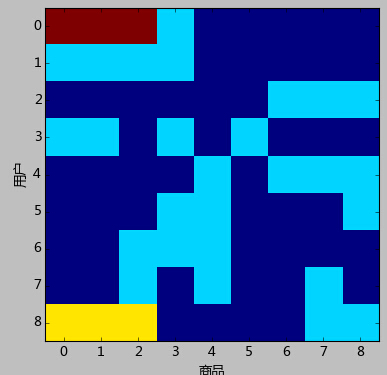
如第一行对应着用户1购买了商品1，数量为3。可以认为该数据是一个稀疏矩阵。该矩阵可视化出来结果如下：

 

上图中每一行代表一个用户，每一列代表一个商品，对应的颜色不同表示购买的数量不同，深蓝色表示购买数为0。

从图上很容易看出，用户0与用户1同时购买了商品0，1，2，仅仅数量不一样；而商品0和商品1售出的情况一模一样——只被用户0，1，3，8购买过，看上去就像是捆绑销售的一般。

3、代码与分析

 

# -*- coding: utf-8 -*-
from matplotlib import pyplot
import scipy as sp
import numpy as np
from matplotlib import pylab
from sklearn.datasets import load_files
from sklearn.cross_validation import train_test_split
from sklearn.metrics import precision_recall_curve, roc_curve, auc
from sklearn.metrics import classification_report
 
import time
from scipy import sparse
 
start_time = time.time()
 
#计算向量test与data数据每一个向量的相关系数，data一行为一个向量
def calc_relation(testfor, data):
    return np.array(
        [np.corrcoef(testfor, c)[0,1]
         for c in data])
 
# luispedro提供的加速函数:
def all_correlations(y, X):
    X = np.asanyarray(X, float)
    y = np.asanyarray(y, float)
    xy = np.dot(X, y)
    y_ = y.mean()
    ys_ = y.std()
    x_ = X.mean(1)
    xs_ = X.std(1)
    n = float(len(y))
    ys_ += 1e-5  # Handle zeros in ys
    xs_ += 1e-5  # Handle zeros in x
    return (xy - x_ * y_ * n) / n / xs_ / ys_
 
        
#数据读入
data = np.loadtxt('1.txt')
x_p = data[:, :2] # 取前2列
y_p = data[:,  2] # 取前2列
x_p -= 1          # 0为起始索引
y = (sparse.csc_matrix((data[:,2], x_p.T)).astype(float))[:, :].todense()
nUser, nItem = y.shape
 
 
#可视化矩阵
pyplot.imshow(y, interpolation='nearest')
pyplot.xlabel('商品')
pyplot.ylabel('用户')
pyplot.xticks(range(nItem))
pyplot.yticks(range(nUser))
pyplot.show()
 
 
#加载数据集，切分数据集80%训练，20%测试
x_p_train, x_p_test, y_p_train, y_p_test = \
          train_test_split(data[:,:2], data[:,2], test_size = 0.0)    
x = (sparse.csc_matrix((y_p_train, x_p_train.T)).astype(float))[:, :].todense()
    
 
Item_likeness = np.zeros((nItem, nItem))
 
#训练    
for i in range(nItem):
    Item_likeness[i] = calc_relation(x[:,i].T, x.T)
    Item_likeness[i,i] = -1        
        
for t in range(Item_likeness.shape[1]):
    item = Item_likeness[t].argsort()[-3:]
    print("Buy Item %d will buy item %d,%d,%d "%
          (t, item[0], item[1], item[2]))
 
print("time spent:", time.time() - start_time)

输出如下：

Buy Item 0, recommond item 3,2,1 
Buy Item 1, recommond item 3,2,0 
Buy Item 2, recommond item 3,0,1 
Buy Item 3, recommond item 0,1,5 
Buy Item 4, recommond item 6,7,8 
Buy Item 5, recommond item 0,1,3 
Buy Item 6, recommond item 4,7,8 
Buy Item 7, recommond item 4,8,6 
Buy Item 8, recommond item 4,7,6 
time spent: 1.9111089706420898

代码中，我们计算了每一个Item与其他所有item的相关性，然后排序选取最大的前3个作为推荐。

最需要注意的是，真正的应用中，大量的用户与大量的商品之间建立矩阵，计算量是巨大的。从皮尔森相关系数的定义来看，其计算量也是巨大的。因此代码中给了luispedro提供的一种计算相关系数的替换函数，效率能提高不少。